Главная | Обратная связь

Загальна постановка задач лінійного програмування

 

Лінійним обмеженням, накладеним на змінні , називається співвідношення одного з наступних трьох типів:

де 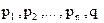- дійсні числа.

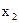Наприклад, співвідношення 2х - ≤ 1 або ≥ 0 є

лінійними, а співвідношення 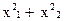≥3 або sin x₁ ≤ 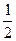не є лінійними.

Загальна постановка задачі лінійного програмування (ЗЛП) полягає в наступному.

 

Дано деяку лінійну функцію

f = _n (2.1)

і деяка система лінійних обмежень, накладених на змінні :

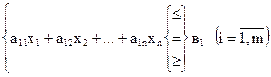(2.2)

Потрібно знайти такі значення змінних , які

задовольняли б обмеженням (2.2) і при цьому обертали б в оптимум (max і min) функцію (2.1).

Функція (2.1) називається цільовою. Кожний набір значень змінних, при яких задовольняються обмеження (2.2), називається припустимим рішенням або припустимим планом ЗЛП. Сукупність всіх припустимих рішень називається областю припустимих рішень (ОПР).

Наведені в параграфах 2.1, 2.2, 2.3 задачі є задачами лінійного програмування.

Припустиме рішення, що обертає цільову функцію в оптимум, називається оптимальним рішенням або оптимальним планом.

Говорять, що ЗЛП розв'язна, якщо вона має оптимальний план. У протилежному випадку задача називається нерозв'язною.

ЗЛП може бути нерозв'язною тільки з наступних двох причин:

а) ОПР порожня;

б) ОПР непорожня, але цільова функція не обмежена на ОПР зверху, якщо в ЗЛП шукається її максимум, або - не обмежена знизу, якщо в ЗЛП шукається мінімум цільової функції.

Наприклад, задача: f = 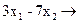min

при обмеженнях

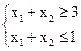
нерозв'язна через порожнечу ОПР.

Задача ж f = 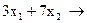max при обмеженні

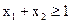нерозв'язна через те, що цільова функція не обмежена зверху на ОПР. (Щоб переконатися в цьому, розгляньте такі припустимі рішення : і т.д.).

 

Геометричний метод вирішення ЗЛП

 

У випадку, коли число змінних у ЗЛП дорівнює двом, завдання можна вирішити геометрично. Розглянемо приклади.

 

Приклад 1

f = max

Кожне припустиме рішення ЗЛП будемо зображувати точкою координатної площини. Побудуємо ОПР (рис. 2.1). Розглянемо перше лінійне обмеження . Сукупність точок площини, що задовольняють цьому обмеженню, являє собою напівплощину, обмежену прямою 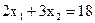. Спочатку побудуємо цю граничну пряму (її можна побудувати по двох точках: (0,6) і (9,0). Ця пряма розіб'є площину на дві напівплощини. Щоб вирішити питання про те, яку із цих двох напівплощин визначає нерівність , візьмемо в одній з напівплощин яку-небудь точку, що не лежить на граничній прямій, і підставимо її координати в нерівність. Наприклад, за таку точку візьмемо початок координат - точку (0,0). Оскільки 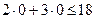, то напівплощина, обумовлена нерівністю , містить точку (0,0). Аналогічно знаходимо напівплощини, обумовлені іншими обмеженнями. Далі визначимо ОПР як загальну частину отриманих напівплощин. Одержимо опуклий багатокутник

 

Рис.2.1.

Тепер залишилося визначити максимум цільової функції на ОПР. Для цього побудуємо лінії рівня цільової функції. Лінія рівня - це безліч точок площини, у яких цільова функція приймає постійне значення. Оскільки цільова функція

f = 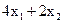,то кожна лінія рівня має вигляд 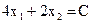. Бачимо, що при різних значеннях параметра С маємо паралельні прямі. Побудуємо, наприклад, дві лінії рівня, поклавши С = 4 і С = 8. Відзначимо стрілкою напрямок, у якому переміщається лінія рівня при збільшенні С. Пересуваючи лінію рівня в зазначеному напрямку, знайдемо точку ОПР, у якій С має найбільше значення. Це буде точка А. Вона є результатом перетинання двох прямих: 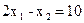і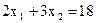

Для знаходження координат точки А вирішимо систему

Одержимо оптимальне рішення

 

Приклад 2. f = 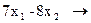min

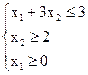
рис. 2.2.

 

У цьому прикладі напівплощини, обумовлені лінійними обмеженнями, не мають загальних точок. Тому ЗЛП нерозв'язна через порожнечу ОПР.

Приклад 3. f =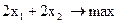

У даному прикладі (рис.2.3) ОПР - опукла необмежена багатокутна область.

 

рис. 2.3.

 

Побудуємо лінію рівня 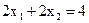. Пересуваючи лінію рівня в напрямку, зазначеному стрілкою, бачимо, що на ОПР цільова функція може приймати які завгодно великі значення. Тому ЗЛП нерозв'язна через необмеженість зверху на ОПР цільової функції.

 

Приклад 4. f =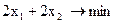

Цей приклад відрізняється від попереднього тільки тим, що цільову функцію потрібно мінімізувати, а не максимізувати. Лінію рівня потрібно переміщати в напрямку, протилежному тому, що зазначено на рисунку 2.3 стрілкою. Оскільки лінія рівня паралельна прямій 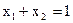, то мінімальне значення на ОПР цільова функція досягає у всіх точках відрізка АВ. Щоб указати конкретне оптимальне рішення задачі, потрібно виписати координати якої-небудь точки цього відрізка.

Наприклад,

Приклад 5. Вирішимо геометрично задачу про використання

обладнання, що розглядалася в параграфі 2.1. Її математична модель

f =

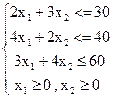
Побудуємо ОПР (рис 2.4). Потім проведемо лінію рівня 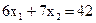. Укажемо стрілкою напрямок, у якому переміщається лінія рівня 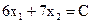із збільшенням C. Максимум цільової функції на ОПР досягається в точці А. Для відшукання координат точки А вирішимо систему:

 

 

рис.2.4.

 

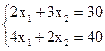
Звідси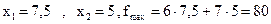

Відповідь. Оптимальний план такий: виробів А потрібно робити 7,5 одиниць, виробів В -5 одиниць; при цьому прибуток буде дорівнювати 80 грошовим одиницям.

Геометричний метод можна використовувати для вирішення ЗЛП із числом змінних n = 3. При більшому числі змінних ЗЛП не допускає наочного геометричного вирішення. Разом з тим для довільного числа змінних справедливі твердження:

1) область припустимих рішень являє собою опуклий багатогранник;

2) якщо ЗЛП розв'язна, то оптимальне рішення досягається в одній з вершин опуклого багатогранника.