 |
|
Канонічний вигляд ЗЛП
У вихідній постановці ЗЛП можуть допускати різні форми запису. Так, в одних задачах потрібно максимізувати цільову функцію, в інших - мінімізувати; деякі лінійні обмеження можуть мати вигляд рівностей, інші - нерівностей і т.д.
Для однаковості запису ЗЛП уводиться так звана канонічна форма запису.
Говорять, що ЗЛП записано в канонічній формі, якщо вона має такий вигляд:
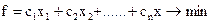 (2.3)
(2.3)

Відзначимо наступні особливості канонічного виду:
1) потрібно мінімізувати цільову функцію;
2) всі лінійні обмеження, крім вимог невід’ємності змінних, мають вигляд рівностей;
1) на всі змінні накладені вимоги невід’ємності .
Покажемо, що будь-яку ЗЛП можна привести до канонічного виду.
1) Якщо в ЗЛП потрібно максимізувати цільову функцію f, то покладемо g = - f і зажадаємо мінімізувати функцію g. Вийде нова ЗЛП, що еквівалентна вихідній в тому розумінні, що кожне оптимальне рішення вихідної задачі буде оптимальним рішенням нової задачі і навпаки.
2) Припустимо, що в ЗЛП є лінійне обмеження виду
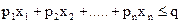 . Замінимо таке обмеження наступними двома обмеженнями:
. Замінимо таке обмеження наступними двома обмеженнями:

де z - нова змінна, котра в цільову функцію вводиться з коефіцієнтом 0 (інакше кажучи, змінна z не вводиться в цільову функцію). Значення змінної z можна не враховувати після вирішення нової задачі.
Аналогічно, обмеження виду 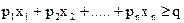 заміняється двома обмеженнями:
заміняється двома обмеженнями:
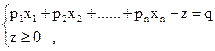
3) Припустимо, що в ЗЛП не до всіх змінних пред'явлена вимога невід’ємності. Тоді кожну змінну 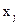 , на яку не накладена вимога невід’ємності , представимо у вигляді різниці двох невід’ємних змінних:
, на яку не накладена вимога невід’ємності , представимо у вигляді різниці двох невід’ємних змінних:
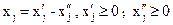 (2.6)
(2.6)
Кожне входження змінної  в цільову функцію або обмеження замінимо різницею
в цільову функцію або обмеження замінимо різницею  . Вирішивши нову задачу за допомогою (2.6), повернемося до колишніх змінних.
. Вирішивши нову задачу за допомогою (2.6), повернемося до колишніх змінних.
Зазначеними прийомами будь-яка ЗЛП приводиться до канонічного виду.
Приклад. Привести до канонічного виду
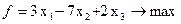

Проробимо описані дії.
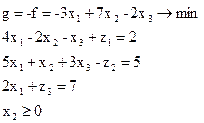
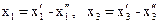
Тепер одержимо ЗЛП у канонічному виді:
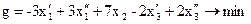
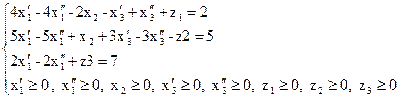
2.7. Поняття опорного плану ЗЛП.
Нехай ЗЛП задана в канонічному вигляді (2.3 - 2.5). Припустимо, що система рівнянь (2.4) приведена до жорданової форми з невід’ємними правими частинами:
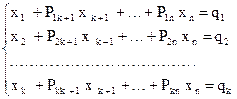 (2.6)
(2.6)
де 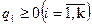 .
.
Дорівнявши до нуля вільні змінні, одержимо базисне рішення системи (2.4)
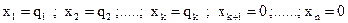 (2.7)
(2.7)
У силу умови  набір значень змінних (2.7) задовольняє й обмеженням (2.5). Тому (2.6) є припустимим рішенням ЗЛП.
набір значень змінних (2.7) задовольняє й обмеженням (2.5). Тому (2.6) є припустимим рішенням ЗЛП.
Припустиме рішення (2.7) називається базисним припустимим рішенням або опорним планом ЗЛП. При цьому говорять, що змінні 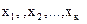 складають припустимий базис.
складають припустимий базис.
Виявляється, що якщо ОПР зобразити геометрично, то кожний опорний план ЗЛП відповідає вершині багатогранника. Тому справедлива наступна теорема.
Якщо ЗЛП розв'язна, то існує оптимальний опорний план.