 |
|
ЦИФРОВАЯ ФИЛЬТРАЦИЯ
Цифровая фильтрация применяется для сглаживания информации, измеряемой аналого-цифровым преобразователем (АЦП) на выходе исследуемого блока или системы управления при натурных испытаниях в лабораторных или промышленных условиях, а также в реальных системах управления, в частности, при идентификации объекта управления (определении параметров его модели).
При фильтрации (оценивании информации) могут использоваться как аналоговые, так ицифровые фильтры. Любая ЭВМ, в частности микроЭВМ, рассматривается как цифровой фильтр, а с использованием АЦП на входе — как фильтр дискретных данных.
В настоящее время известно много формул цифровой фильтрации, отличающихся различной степенью сложности (фильтры Калмана, Винера, Чебышева и др.).
Однако, начиная с Калмана, объект управления перестал быть "черным ящиком". Он предложил рекуррентные формулы цифровой фильтрации, которые вывел из известной формулы оценки среднего (математического ожидания)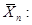 
(4.1)
где 
— i-ое текущее значение входного сигнала
По аналогии с (4.1) запишем:
(4.2)
Подставим (4.1) в (4.2) и преобразуем:
Обозначим:
Тогда
. (4.3)
Очевидно, что
Отсюда 
. Окончательно имеем:
. (4.4)
Раскроем и преобразуем (4.4):
. (4.5)
Формулы (4.3) — (4.5) называются 
фильтрами. При сглаживании информации с помощью 
фильтров требуется запоминать предыдущее усредненное значение 
и измеренное новое значение 
. Коэффициенты 
и 
могут быть заложены в постоянное запоминающее устройство. Такие фильтры эффективно используются для целей управления. Однако при их использовании необходимо знать динамику объекта и статистику шумов, чтобы избежать значительных ошибок при оценке.
Поэтому будем использовать упрощенную формулу (4.3) при 
, но с дополнительными ограничениями. Заметим, что при 
формула (4.3) дает скользящее среднее. При этом
(4.6)
Дополнительные ограничения, при которых оценка по двум измерениям будет достоверной, можно получить из следующих рассуждений. Два измерения, следующие друг за другом, могут отличаться для инерционного процесса на величину:
Можно считать, что это приращение всегда обусловлено шумами в (n-1) и n измерениях, а полезные сигналы равны даже в том случае, когда они по каким-либо причинам сильно отличаются друг от друга (внезапное изменение входного сигнале, обрыв датчика и т.п.). Поэтому в качестве оценки поведения входного сигнала можно выбрать соотношение:
, (4.7)
где 
— допустимая ошибка между двумя измерениями, следующими друг за другом.
В качестве дополнительных ограничений с целью повышения надежности рекомендуется использовать следующее неравенство:
, (4.8)
где 
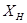и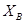 
— соответственно минимально и максимально возможные значения входных параметров.
Задание
1. Составить схему алгоритма и процедуру сглаживания входного массива 
выхода объекта управления, используя файл данных, полученный в разделе 3.
2. Вывести на печать исходный массив и сглаженный 
.
Рекомендации
1. В процедуре цифровой фильтрации сигнала необходимо вычислить коэффициент усиления модели объекта kМ, а затем 
и XВ, который зависит от kМ.
2. Для облегчения анализа и получения более структурированной программы целесообразно ввести 3 локальные логические переменные z1, z2, z3:
z1 = 
;
z2 = z1 
;
z3 = z1 
,
где с – счетчик ненулевых значений.
3. Логические переменные по П.2 вычисляются и анализируются в цикле FOR – DO, начиная с i := 1.
4. Анализ следует производить начиная с состояния счетчика ошибок ERROR. Количество ошибок исходных данных не должно превышать 3. Если счетчик ошибок равен 3, то на экран должно выводиться сообщение: «Сбой исходных данных» и осуществляется остановка программы.
5. Далее надо анализировать z1: если z1 ложно, то в счетчик ERROR добавляется «1», а берется равным предыдущему значению 
, после чего анализ переходит к следующему циклу. Если z1 истина, то осуществляется переход к анализу логической переменной z2.
6. Если z2 истина, то в счетчик нулевых интервалов n1 добавляется «1», а берется равным 
, в противном случае счетчик ненулевых значений увеличивается на «1», а значение берется равным .
7. И наконец, последний анализ: если z3 истина, то можно находить сглаженное значение по формуле (4.6).
8. В этой же процедуре можно вычислить время запаздывания объекта: 
.