Главная | Обратная связь

Теоретическое введение

Те­п­ло­вое хао­ти­че­ское дви­же­ние мо­ле­кул га­за спо­соб­ст­ву­ет сгла­жи­ва­нию вся­ких раз­ли­чий ме­ж­ду рав­ны­ми час­тя­ми га­за. По­это­му, ес­ли мы име­ем слои га­за, дви­жу­щие­ся с раз­лич­ны­ми по ве­ли­чи­не ско­ро­стя­ми, то на упо­ря­до­чен­ное дви­же­ние сло­ев га­за с раз­лич­ны­ми ско­ро­стя­ми на­кла­ды­ва­ет­ся хао­ти­че­ское дви­же­ние мо­ле­кул. Мо­ле­ку­лы пе­ре­хо­дят из слоя, дви­жу­ще­го­ся со ско­ро­стью v₁, в слой, дви­жу­щий­ся со ско­ро­стью v₂, и об­рат­но, пе­ре­но­ся при этом им­пульс. Та­кой про­цесс пе­ре­но­са им­пуль­са, вы­рав­ни­ваю­щий ско­ро­сти от­дель­ных сло­ев, со­про­во­ж­да­ет­ся пре­вра­ще­ни­ем ки­не­ти­че­ской энер­гии упо­ря­до­чен­но­го дви­же­ния дан­но­го слоя в энер­гию те­п­ло­во­го дви­же­ния мо­ле­кул и на­зы­ва­ет­ся внут­рен­ним тре­ни­ем. За­кон Нью­то­на для внут­рен­не­го тре­ния имеет вид:

. (12.1)

Здесь η – коэффициент вязкости, численно равный силе вязкого трения между двумя слоями единичной площади при единичном градиенте скоростей. Этот за­кон мож­но вы­вес­ти, ис­поль­зуя ос­нов­ные по­ло­же­ния мо­ле­ку­ляр­но-ки­не­ти­че­ской тео­рии. Пусть у нас име­ют­ся два слоя га­за, дви­жу­щие­ся со ско­ро­стя­ми v₁и v₂ (рис.12.1). Выделим мысленно в среде какую-то площадку ΔS и напра­вим ось zортогонально к ней. Две другие оси х и у параллельны площад­ке. Хаотичность движения молекул смоделируем следующим образом. Будем считать, что ровно 1/3 молекул движется вдоль оси х, 1/3 – вдоль оси у и 1/3 – вдоль оси z. Из молекул, ле­тящих параллельно z, ровно полови­на(1/6 часть полного числа молекул) движется в положительном направле­нии, и столько же – в отрицательном. Подсчитаем количество молекул N, пе­ресекающих площадку ΔS в единицу времени. Ясно, что молеку­лы, летящие вдоль осей х и у,площад­ку не пересекут. За время Δt молекулы преодолевают расстояние , где – средняя арифметическая скорость. По­тому на площадку попадет только 1/6 часть молекул из объема , то есть

, (12.2)

где – концентрация молекул.

Импульс, пе­ре­но­си­мый по­то­ком мо­ле­кул за время Δt через площадку ΔS в по­ло­жи­тель­ном на­прав­ле­нии оси zиз слоя, дви­жу­ще­го­ся со ско­ро­стью v₁ (рис.12.2), раве­н:

, (12.3)

где 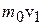– импульс одной молекулы, связанный с направленным движением молекул.

Импульс, переносимый в противоположном направлении, равен

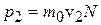. (12.4)

Полное из­ме­не­ние им­пуль­са слоя получим из (12.2-12.4):

. (12.5)

Последний раз перед попаданием на площадку ΔS молекулы сталкивались с другими молекулами на расстоянии длины свободного пробега λ от площадки. Поэтому к выделенной нами площади они подходят с теми импульсами частиц, которые сложились в точках с координатами (z–λ)и (z+λ)соответственно (z – координата площадки) и соответствуют скоростям направленного движения v₂ и v₁ (рис.12.2).

Поскольку длина свободного пробега λ мала, то раз­ность ско­ро­стей мож­но вы­ра­зить че­рез гра­ди­ент ско­ро­сти и дли­ну сво­бод­но­го про­бе­га мо­ле­кул l:

. (12.6)

Учи­ты­вая, что nm₀=r (плот­ность ве­ще­ст­ва), из (12.5) и (12.6) получим:

. (12.7)

По второму закону Ньютона из­ме­не­ние им­пуль­са те­ла равно им­пуль­су си­лы: , тогда

. (12.8)

Мы вывели закон Ньютона (12.1) для вязкости и получили выражение для коэффициента динамической вязкости:

. (12.9)

Теперь можно установить зависимость вязкости газа от температуры: поскольку средняя арифметическая скорость

, (12.10)

а длина свободного пробега молекул

, (12.11)

то при постоянной концентрации молекул (например, в изохорном процессе) вязкость с повышением температуры увеличивается пропорционально .

Получим выражение для расчёта средней длины свободного пробега молекул из (12.9) с учётом (12.10):

. (12.12)

Плотность газа выразим из уравнения Менделеева-Клапейрона 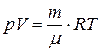: , тогда из (12.12): , или

, (12.13)

где p=10⁵ Па – атмосферное давление; μ=0.029 кг/моль – молярная масса воздуха; R – универсальная газовая постоянная.