Главная | Обратная связь

Нормальный закон распределения (закон Гаусса)

Существуют различные виды распределения случайных величин. Однако особое значение в теории вероятностей и в различных практических приложениях имеет нормальный закон распределения (закон Гаусса), характеризующийся тем, что для него среднее арифметическое значение случайной величины является также и наиболее вероятным. Закон Гаусса применяют, если выполняются следующие требования:

1. Величина может принимать непрерывный ряд значений.

2. При большом числе наблюдений отклонения от среднего одинаковой величины, но разного знака встречаются одинаково часто.

3. Большие отклонения от среднего встречаются реже, чем малые.

Плотность вероятности для нормального закона распределения описывается формулой:

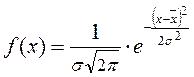, (11.16)

где – математическое ожидание случайной величины, σ – среднее квадратическое отклонение.

Кривая нормального закона распределения имеет колоколообразную форму (рис.11.1), симметричную относительно вертикальной прямой x= 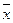. С уменьшением σ кривая становится все более островершинной. Площадь, заключенная под всей кривой, согласно условию нормировки (11.12), равна единице.

Удобно привести функцию Гаусса (11.16) к виду (11.17), если ввести безразмерную переменную :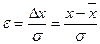

. (11.17)

Тогда вероятность того, что х отклоняется от не больше, чем на Δх, можно рассчитать так:

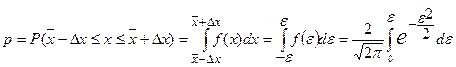. (11.18)

Результаты вычисления р по формуле (11.18) приведены в табл. 11.1.

 

Таблица 11.1

e	р	e	р	e	р
		0.4	0.31	2.0	0.95
0.1	0.08	0.5	0.38	2.5	0.988
0.2	0.16	1.0	0.68	3.0	0.997
0.3	0.24	1.5	0.87	4.0	0.99993

 

Очевидно, чем больше Δх, то есть чем больше ε, тем больше вероятность того, что случайная величина принимает значение в интервале от –Δх до +Δх. Так, например, вероятность того, что случайная величина принимает какое-либо значение в интервале от –σ до +σ (ε=1), из (11.11):

,

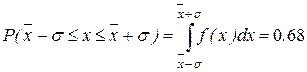то есть заштрихованная на рис.11.1 площадь равна 0.68. Если ε=2, то вероятность того, что случайная величина отклоняется от среднего значения (математического ожидания) не больше, чем на Δх=2σ, равна 95%, а отклонение случайной величины на Δх=3σ (ε=3) происходит с вероятностью 99.7%.

Закону Гаусса подчиняется распределение молекул газа по компонентам скоростей. Если газ находится в состоянии равновесия, в нем устанавливаются постоянные давление и температура. При этом молекулы газа движутся беспорядочно, сталкиваясь между собой и со стенками сосуда, беспрерывно меняя свою скорость. Несмотря на полную хаотичность молекулярных движений, их распределение по скоростям оказывается вполне определенным, если число молекул газа достаточно велико. На характер распределения не влияют ни столкновения между молекулами, ни внешние поля. Оно оказывается однозначным и единственно возможным.

Как бы ни изменялись скорости различных молекул, среднее значение квадрата скорости остается постоянным и равно

, (11.19)

где m₀ – масса молекулы, Т – термодинамическая температура газа, k – постоянная Больцмана. Введём функцию распределения по компонентам скоростей: j(v_x)dv_x= – доля молекул, проекции скорости которых на ось ОХ лежат в интервале от v_х до v_х+dv_х. Хаотичность движения молекул позволяет принять для проекции скорости v_х молекулы нормальный закон распределения. Как показал Д.К.Максвелл, плотность вероятности того, что молекула имеет компоненту скорости v_х, равна:

, (11.20)

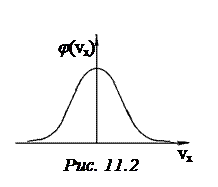График функции распределения по компонентам скоростей изображен на рис.11.2.

Функция принимает максимальное значение при v_x=0 и симметрична относительно оси ординат. Это значит, что среднее значение проекции скорости и ее наиболее вероятное значения равны нулю. Доля молекул, движущихся в данный момент времени в плоскости, перпендикулярной оси ОХ, максимальна.

Поскольку все направления движения молекул в пространстве равноправны, выражения для j(v_y) и j(v_z) аналогичны выражению (11.20). Вероятность того, что молекула имеет проекцию скорости, лежащую в интервале от v_х до v_х+dv_х:

. (11.21)