Уравнение Шредингера

Обнаружение волновых свойств микрочастиц делало необходимым создание новой механики, которая бы могла описать данные свойства. Эта механика получила название квантовой.

Основным уравнением квантовой механики является уравнение Шредингера:

, (2)

которое нельзя вывести из каких-либо известных ранее соотношений, аналогично второму закону Ньютона в классической механике. Его следует рассматривать как исходное основное предположение, справедливость которого доказывается тем обстоятельством, что все вытекающие из него следствия самым точным образом согласуются с опытными фактами. Состояние микрочастицы в этом уравнении описывается так называемой волновой функцией Y(x, y, z, t) – пси функцией, которая может быть найдена путем решения данного уравнения. Остальные величины, входящие в эго уравнение, имеют следующие значения: i – мнимая единица; 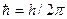(h–постоянная Планка), m – масса частицы, D – оператор Лапласа ( 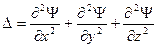), U – потенциальная энергия частицы.

Как следует из уравнения (2), вид волновой функции Y определяется потенциальной энергией U, т. е., в конечном счете, характером тех сил, которые действуют на частицу. В общем случае, U есть функция координат и времени. Для стационарного силового поля U волновая функция Y распадается на два множителя, одни из которых зависит только от времени, а второй – только от координат:

, (3)

где Е – полная энергия частицы.

В самом деле, подстановка функции (3) в уравнение (2) дает:

.

Сокращая все члены этого уравнения на общий множитель и произведя соответствующие преобразования получим дифференциальное уравнение, определяющее функцию :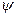

(4)

Уравнение (4) называется уравнением Шредингера для стационарных состояний. В дальнейшем мы будем называть его просто уравнение Шредингера.

К уравнению Шредингера можно прийти путем следующих рассуждений. Из опытов по дифракции микрочастиц вытекает, что параллельный пучок частиц обладает свойствами плоской волны, распространяющейся в направлении движения частиц. Уравнение плоской волны, распространяющейся в направлении оси х имеет, как известно, записывается или в комплексном виде:

, (5)

подразумевая, что надо принимать во внимание вещественную часть этого выражения.

Согласно гипотезе де-Бройля свободному движению частицы соответствует плоская волна с частотой и длиной волны . Заменяя w и р в выражении (5) энергией и импульсом частицы в соответствии с (1), получим волновую функцию для свободной частицы, движущейся в направлении оси х:

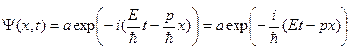. (6)

Чтобы найти дифференциальное уравнение, которому удовлетворяет фуикция (6), воспользуемся соотношением между Е и р: Е = 2р²/m.

Продифференцировав функцию (6) один раз по t a второй раз дважды по х,получим:

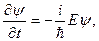
Из этих соотношений можно выразить Е и р² через функцию 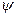и ее производные:

Подставляя последние выражения в соотношение Е = 2р²/m получим дифференциальное уравнение:

.

В общем случае, если направление волны не совпадает с осью х фаза колебаний будет зависеть от всех координат: х, у и z и уравнение будет совпадать с уравнением Шредингера (4) для случая U = 0 (частица по условию свободна):

. (7)

Таким образом, мы получили уравнение Шредингера для свободно движущейся частицы. Теперь следует обобщить уравнение (7) на случай частицы, движущейся в потенциальном поле сил, когда полная энергия Е слагается из кинетической энергии Т и потенциальной энергии U: E = T + U. Произведя такую замену, мы придем к уравнению (4).

Необходимо, однако, подчеркнуть, что приведенные рассуждения не могут рассматриваться как вывод уравнения Шредингера. Их цель – пояснить, каким образом можно было прийти к установлению вида волнового уравнения для микрочастицы. Доказательством же правильности уравнения Шредингера может служить лишь согласие с опытом тех результатов, которые получаются с помощью этого уравнения.

3. Квантово-механическое описание движения микрочастиц

Соотношение между волновой функцией 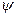и описываемой ею частицей аналогично соотношению между световой волной и фотоном. Для волны было установлено, что квадрат амплитуды световой волны определяет вероятность попадания фотона в соответствующую точку пространства. Точно так же квадрат модуля волновой функции (волновая функция может оказаться комплексной) для какой-либо точки пространства, будучи умножен на включающий в себя эту точку элемент объема dV, определяет вероятность dP того, что частица будет обнаружена в пределах объема dV:

. (8)

Таким образом, физический смысл функции 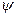заключается в том, что квадрат ее модуля дает плотность вероятности (вероятность, отнесенную к единице объема) нахождении частицы в соответствующем месте пространства. Для стационарных состояний волновая функции имеет вид (3) и так что в этом случае плотность вероятности равна и, следовательно, от времени не зависит.

Из сказанного вытекает, что квантовая механика имеет статистический характер. Она не позволяет определить местонахождение частицы в пространстве или траекторию, по которой движется частица. С помощью волновой функции можно лишь предсказать, с какой вероятностью частица может быть обнаружена в различных точках пространства.

На первый взгляд может показаться, что квантовая механика дает менее точное описание движения частицы, чем классическая механика, которая определяет «точно» местоположение и скорость частицы в каждый момент времени. Однако в действительности это не так. Квантовая механика гораздо глубже вскрывает истинное поведение микрочастиц. Она лишь не определяет того, чего нет на самом деле. В применении к микрочастицам понятия определенного местоположения и траектории вообще теряют смысл. Движение по определенной траектории несовместимо с волновыми свойствами, что становится совершенно очевидным, если проанализировать существо опытов по дифракции.

Рассмотрим дифракцию от двух близко расположенных отверстий (рис. 5). Вследствие интерференции волн, распространяющихся от отверстий, дифракционная картина не будет тождественна наложению дифракционных картин, получающихся от каждого из отверстий в отдельности (картина, получающаяся в случае рис. 5, а не совпадает с наложением картин, получающихся в случаях би в).Следовательно, вероятность попадания электрона (или какой-либо другой микрочастицы) в различные точки экрана при прохождении пучка через оба отверстия также не будет равна сумме вероятностей для случаев прохождения пучка через каждое из отверстий в отдельности. Отсюда неизбежно следует вывод, что на характер движения каждого электрона оказывают влияние оба отверстия. Такой вывод не совместим с представлением о траекториях. Если бы электрон в каждый момент времени находился в определенной точке пространства и. двигался по траектории, он проходил бы через определенное отверстие – первое иливторое. Явление же дифракции доказывает, что в прохождении каждого электрона участвуют оба отверстия: ипервое, ивторое.

Рис. 5.

Не следует, однако, представлять дело так, что какая-то часть электрона проходит через одно отверстие, а другая часть – через второе. Электрон, как и другие микрочастицы, всегда обнаруживается как целое, с присущей ему массой, зарядом и другими характерными для нею величинами. Таким образом, электрон, протон, атомное ядро представляют собой частицыс весьма своеобразными свойствами. Обычный шарик, даже и очень малых размеров (макроскопическая частица), не может служить прообразом микрочастицы. С уменьшением размеров начинают проявляться качественно новые свойства, не обнаруживающиеся у макрочастиц.

В ряде случаев утверждение об отсутствии траекторий у микрочастиц, казалось бы, противоречит опытным фактам. Так, например, в камере Вильсона путь, по которому движется микрочастица, обнаруживается в виде узких следов (треков), образованных капельками тумана; движение электронов в электроннолучевой трубке превосходно рассчитывается по классическим законам, и т. п. Это кажущееся противоречие объясняется тем, что при известных условиях понятия траектории и определенного местоположения оказываются применимыми к микрочастицам, но только с некоторой степенью точности.

Положение оказывается опять-таки точно таким, как и в оптике. Если размеры преград или отверстий велики по сравнению с длиной волны, распространение света происходит как бы вдоль определенных лучей (траекторий). При определенных условиях понятия положения в пространстве и траектории оказываются приближенно применимыми к движению микрочастиц, подобно тому как оказывается справедливым закон прямолинейного распространения света.

Степень точности, с какой к частице может быть применено представление об определенном положении ее в пространстве, дается соотношением неопределенностей, установленным Ганзенбергом. Согласно этому соотношению частица не может иметь одновременно вполне точные значения, например, координаты х исоответствующей этой координате составляющей импульса р_х, причем неопределенности в значениях этих величин удовлетворяют условию:

. (8)

Такая запись означает, что произведение неопределенностей координаты и соответствующего ей импульса не может быть меньше величины порядка 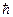. Чем точнее определена одна из величин, х или р_х,тем больше становится неопределенность другой. Возможны состояния частицы, при которых одна из величин имеет вполне точное значение, но тогда вторая величина будет совершенно неопределенной.

Соотношения, аналогичные (8), справедливы для любой координаты и соответствующего ей импульса, а также для ряда других величин, например, для взятых попарно проекций момента импульса на координатные оси.

Чтобы пояснить соотношение неопределенностей, рассмотрим следующий пример. Для определения положения свободно летящей микрочастицы поставим на ее пути щель шириной Dх,расположенную перпендикулярно к направлению движения частицы (рис. 6). До прохождения частицы через щель ее составляющая импульса р_х имеет точное значение, равное нулю (щель по условию перпендикулярна к скорости), так что р_х = 0, зато координата х частицы является совершенно неопределенной.

Рис. 6

В момент прохождения частицы через щель положение меняется. Вместо полной неопределенности координаты х появляется неопределенность Dх, но это достигается ценой утраты определенности значения р_х. Дейтвительно, вследствие дифракции имеется некоторая вероятность того, что частица будет двигаться в пределах угла 2j, где j – угол, соответствующий первому дифракционному минимуму (максимумами высших порядков можно пренебречь, поскольку их интенсивность мала по сравнению с интенсивностью центрального максимума). Таким образом, появляется неопределенность: .

Ранее было установлено, что первому минимуму, получающемуся от щели шириной d,соответствует угол j, для которого . Откуда, с учетом того, что получается соотношение , согласующееся с (8).

Оценим неопределенность координаты и импульса для электрона в электроннолучевой трубке. Пусть след электронного пучка на экране имеет радиус порядка 10^-3 см,длина трубки порядка 10 см, рис. 7. Тогда Dр_х/р_х~10^-4.

Рис. 7

Импульс электрона связан с ускоряющим напряжением U соотношением: р²/2m = еU, откуда

. При напряжении U ~ 10⁴ Вэнергия электрона равна 10⁴ эв = 1,6´ ´10^-8 эрг, импульс будет р = 5 10^-18 г´см/с , а Dр » 5´10^-22г´см/с. Для Dх тогда получим 2 10^-6 см. Полученный результат свидетель-ствует о том, что движение электрона в рассматриваемом случае будет практи-

чески неотличимо от движения по траектории.

Соотношение неопределенностей отражает двойственную корпускулярно-волновую природу микрочастиц. Одного этого соотношения достаточно, чтобы получить ряд важных результатов. В частности, оно позволяет объяснить тот факт, что электрон не падает на ядро атома, а также оценить размеры простейшего атома и минимальную возможную энергию электрона в таком атоме.

Если бы электрон упал на точечное ядро, его координаты и импульс приняли бы определенные (нулевые) значения, что несовместимо с принципом неопределенности. Этот принцип требует, чтобы неопределенность координаты электрона Dr и неопределенность импульса Dр были связаны условием (8). Формально энергия была бы минимальна при r = 0 и р = 0. Поэтому, производя оценку наименьшей возможной энергии, нужно положить Dr » r и Dр » р.Подставив эти значения в (8), получим соотношение , где для определенности вместо знака ³ мы взяли знак =. Энергия электрона в атоме водорода равна . Подставляя сюда из предыдущего соотношения получим, что .

Найдем значение r, при котором Е минимальна, продифференцировав и приравняв производную от энергии нулю:

, откуда следует, что и .

Полученные нами значения совпадает с радиусом первой боровской орбиты водородного атома и энергией его основного состояния.

То обстоятельство, что мы получили точные значения r и Е,является, конечно, просто удачей. Приведенный расчет может претендовать лишь на то, чтобы дать оценку порядка величины r и Е.

⇐ Предыдущая 11 12 13 14 151617 18 19 20 Следующая ⇒