 |
|
Разрешающая способность интерферометра Фабри–Перо.
Пусть на ИФП падают две волны с близкими длинами и +. Каждая из них создает свою интерференционную картину. При достаточно близких длинах волн возникает проблема разрешения (различения) этих двух длин волн по наложенным интерференционным картинам. Разрешающая способность интерферометра
характеризуется минимальной разницей в длинах волн, при которой возможно их разрешение:
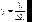. (6.41)
В теории ИФП принимается, что условием разрешения является пересечение кривых, описывающих распределение интенсивности от каждой из волн на половине их максимального значения, т.е. где 
(рис.6.12). Найдем сначала ширину линии на полувысоте из этого условия: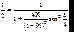 
(6.42)
При большом коэффициенте отражения достаточно мало, так что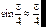 
. Тогда
. (6.43)
Для эталона Фабри–Перо при достаточно больших коэффициентах отражения от пластин получаем значение разрешающей способности:
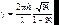. (6.44)
Отсюда видно, что с увеличением разрешающая способность ИФП повышается. Также приводит к увеличению разрешающей способности и увеличение расстояния между пластинами h. Но добиться сколь угодно большой разрешающей способности препятствуют ряд факторов.
Факторы, ограничивающие разрешающую способность:
1. стины ИФП не могут быть сделаны абсолютно плоскими.
2. бходимо добиться параллельности пластин с той же точностью, что и для их плоскостности.
3. стояние между пластинами, умноженное на число эффективных отражений, должно быть меньше, чем длина временной когерентности исследуемого света.
Дисперсионная область. Вспомним, что разность длин волн, при которой наступает перекрытие полос соседних порядков интерференции, называется дисперсионной областью (или областью свободной дисперсии) G (см. раздел по интерференции в тонких пленках). Из определения дисперсионной области следует:
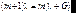. (6.45)
Отсюда получаем: 
. (6.46)
Для ИФП при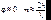 
, поэтому дисперсионная область равна:
. (6.47)
Из сравнения формул для разрешающей способности и дисперсионной области видно, что требование повышения обеих этих величин противоречат друг другу. Для повышения разрешающей способности приходится работать на больших порядках интерференции, т.е. там, где мала дисперсионная область.
Интерференционные фильтры. Интерферометр Фабри-Перо при определенных условиях ( 
) пропускает без ослабления световую волну с определенной длиной, а волны с длинами, лишь немного отличными от такой резонансной длины сильно ослабляются. Т.е. ИФП действует как узкополосный фильтр. Ширина полосы пропускания обычно достигает десятка ангстрем. Следует учесть, что интерференционный фильтр пропускает не только волну с заданной длиной, но и волны с длинами, смещенными на целое число дисперсионных областей, т.е. образующих следующие интерференционные максимумы (в данном случае являющиеся побочными). Поэтому, чтобы разнести побочные максимумы как можно дальше, требуется уменьшать толщину фильтра. Обычно используют оптическую толщину равную половине длины волны. Диэлектрическую пластину этой толщины покрывают с обеих сторон высокоотражающим металлическим либо диэлектрическим (см. ниже) покрытием. Для защиты от повреждений интерференционный фильтр помещают между предохранительными стеклами.
Сканирующий интерферометр Фабри–Перо. Формула Эйри объясняет принцип действия широко используемого в оптике и 
лазерной технике спектрального прибора – сканирующего интерферометра Фабри–Перо. Это своеобразный аналог измерителей частотных характеристик электрических сигналов радиодиапазона, основанных на принципе сканирования резонансной частоты колебательной системы – колебательного контура, коаксиального, полоскового или объемного резонатора. Заметим, что разность фаз линейно зависит от расстояния между пластинами. Если зафиксировать угол , то это соответствует помещению некоторого фотоприемника в любую точку экрана (рис.6.13), где видна интерференционная картина. Оптимальное место для этого – центр картины (точка А), т.к. частотная дисперсия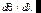 
в этой точке максимальна. Поэтому конечность размеров фотоприемника минимально ухудшает разрешение ИФП как раз при таком местоположении. Теперь допустим, что одна из пластин ИФП параллельно перемещается вдоль оптической оси системы с постоянной скоростью v, т.е. h=h0+vt. Тогда пропускание ИФП становится зависимым от времени, повторяя зависимость функции Эйри. Если на ИФП падает монохроматическая волна, то на осциллографе, развертка которого движется синхронно с пластиной, сигнал от ИФП опишет его аппаратную функцию в соответствии с (6.38). При сложном спектре электрический сигнал опишет исследуемый спектр. На практике перемещение пластин осуществляется или изменением давления газа между пластинами ИФП, или креплением одной из пластин на пьезокерамику. Второй способ предпочтительней, т.к. позволяет осуществить сканирование величины 
электрическим сигналом.
Принцип Фурье-спектроскопии. Пусть излучение немонохроматично и обладает непрерывным спектром. В интервале волновых чисел от k до k+dk интенсивность определяется спектром F(k) и интервалом dk :
. (6.48)
В результате интерференции с учетом разности хода имеем:
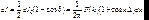.(6.49)
Полная интенсивность определяется интегралом:
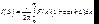(6.50)
Это равенство при =0 примет вид:
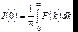. (6.51)
Тогда 
(6.52)
Второе слагаемое в (6.52) f() называется интерферограммой. Обратное преобразование Фурье имеет вид:
. (6.53)
Подставив интенсивность интерферограммы в виде функции разности хода лучей и вычислив f(), с помощью (6.53) получаем спектральный состав излучения. Такой метод определения спектров называется Фурье-спектроскопией. Рассмотрим еще некоторые применения интерференционных явлений в современной 
технике. Просветление оптики. Во многих современных оптических системах используются многочисленные оптические детали (линзы, призмы и др.), отражение от которых ослабляют интенсивность прошедшего света. Поэтому сведение к минимуму френелевских (т.е. рассчитываемых по формулам Френеля) потерь (просветление оптики) становится важной задачей. Явление интерференции позволяет сделать это достаточно эффективно. Для этого на поверхность оптического элемента наносят тонкий слой вещества (пленку), в которой и происходит интерференция (рис.6.14). Пусть n1 – коэффициент преломления внешней среды, из которой падает свет, n2 , h – соответственно коэффициент преломления и оптическая толщина пленки, n3 – коэффициент преломления оптического элемента. Если рассмотреть только двухлучевую интерференцию между волнами 1 и 2, то для полного гашения отраженных пучков, т.е. для полного просветления оптики, необходимо выполнение двух условий:
1) плитуды пучков должны быть равными;
2) разность фаз между ними должна равняться (т.е. волны находятся в противофазе).
Первое условие достигается подбором показателя преломления пленки. Второе условие легко выполняется, если оптическая толщина пленки равна /4.
Более точно и правильнее соотношение для показателя преломления пленки можно найти, рассмотрев аналогично интерферометру Фабри–Перо многолучевую интерференцию. Тогда для относительной интенсивности отраженного от такой системы света получаем (проверить самостоятельно):
, (6.54)
где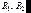 
– амплитудные коэффициенты отражения от первой и второй границ раздела соответственно, – оптическая разность хода между двумя соседними интерферирующими волнами. Положив =, а падение – нормальным, получаем: 
. (6.55)
Т.к. при нормальном падении света 
, то интенсивность отраженного света будет равна нулю, если
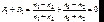. (6.56)
Тогда окончательно получаем условие полного просветления (совместно с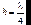 
: 
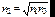. (6.57)
Если первая среда – воздух, а третья – стекло, то удовлетворить этому соотношению весьма трудно, т.к. твердых веществ со столь малым коэффициентом преломления (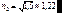 
) в оптическом преломления не существует. Существующие вещества типа виллиолента (NaF), криолита (Na3AlF6) (показатели преломления 
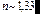) позволяют уменьшить коэффициент отражения до 0,8%. Дальнейшее уменьшение коэффициента отражения может быть достигнуто применением многослойных просветляющих покрытий. Высокоотражающие интерференционные покрытия (интерференционные зеркала).Кроме просветления оптики часто необходимо решить противоположную задачу – увеличить коэффициент отражения от поверхности. Это необходимо, например, при создании лазерных интерференционных зеркал с заданным коэффициентом отражения. Рассматривая систему, аналогичную полученной для просветления оптики, легко убедиться, что если взять показатель преломления диэлектрического слоя больше показателя преломления подложки, а оптическая толщина слоя остается равной /4, то произойдет увеличение коэффициента отражения вследствие взаимного усиления отраженных волн. Но за счет нанесения одного слоя добиться коэффициента отражения больше 30% не удается. Обычно используют многолучевую интерференцию за счет нанесения системы чередующихся слоев с большим и малым показателями преломления. Обычно используют комбинацию сульфида цинка (n = 2,3) и фторида лития (n = 1,3). Для получения коэффициента отражения 99% надо нанести 11 – 13 слоев.
30 Зоны Френеля.Пусть сферическая волна падает на непрозрачный экран с отверстием. Требуется найти распределение интенсивности света за экраном. Для решения этой задачи делаются два предположения:
1) непроницаемые части экрана не являются источниками вторичных волн;
2) в отверстии точки волнового фронта являются такими же источниками вторичных волн, какими они были бы при отсутствии непроницаемых частей экрана.
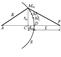
Пусть A – источник сферической волны, S – волновой фронт в некоторый момент времени, R – радиус кривизны этого фронта (рис.7.2). Найдем интенсивность в точке P с помощью принципа Гюйгенса – Френеля. Разобьем поверхность S на кольцеобразные зоны такого размера, чтобы расстояния от краев зоны (в разрезе это соответствует точкам M1, M2, M3 , …) до P отличались на /2 (эти зоны называются зонами Френеля):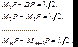 
(7.3)
Из геометрии рис.7.3 можно получить для радиуса m–й зоны Френеля rm :
(7.4)
Исключая величину dm и пренебрегая слагаемыми 2 ввиду их малости, получаем:
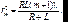(7.5)
Площади всех зон Френеля примерно одинаковы (в случае пренебрежения кривизной поверхности, что не вносит существенной ошибки, если радиусы зон Френеля много меньше радиуса кривизны волнового фронта (обычно это справедливо для очень большого числа зон Френеля)):
(7.6)
Графическое вычисление амплитуды (метод векторных диаграмм).Разделим каждую из зон на большое число N участков. Между началом и концом зоны фаза меняется на , а между малыми участками – на = /N . Пусть E0 – амплитуда волны, приходящей в точку наблюдения P от каждого участка; а фаза волны, приходящей из точки D в точку P – равна нулю. Комплексная амплитуда волны в точке P от центральной зоны Френеля с учетом интерференции равна:
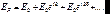(7.7)
Аналитическое сложение амплитуд можно проделать графически, изображая комплексную амплитуду в виде вектора (рис.7.3). При увеличении числа разбиений до бесконечности ломаная кривая превращается в плавную. Длина вектора DM1 пропорциональна амплитуде волны в точке P, когда открыта вся центральная зона Френеля. Аналогично продолжая построение, можно получить кривую, по которой легко определить амплитуду волны (и ее интенсивность), зная соотношение диаметров открываемого отверстия и зон Френеля. При строгом равенстве амплитуд в (7.7) складываемых колебаний от элементарных участков результирующая амплитуда от двух открытых соседних зон была бы равна нулю, т.е. вторичные волны в результате интерференции гаси ли бы друг друга, но коэффициент наклона K() в (7.1) убывает по мере увеличения и приводит к уменьшению амплитуд вторичных волн. Поэтому полученная кривая не замыкается, а имеет вид спирали. Зависимость амплитуды поля в точке P от радиуса отверстия показана на рис.7.4.
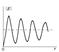Пятно Пуассона.Если на пути световой волны стоит непрозрачный круглый экран, то за экраном в его тени на оси возникает светлое пятно, называемое пятном Пуассона. Необходимость возникновения светлого пятна очевидна из рассуждений по методу зон Френеля. Экран закрывает некоторое число зон Френеля начиная с центральной. Однако следующие зоны после последней из закрытых создают в точке P освещенность, значение которой можно рассчитать с помощью спирали. Т.о., получается, что волна как бы огибает непрозрачный экран. Интенсивность пятна Пуассона весьма слаба при больших размерах непрозрачного экрана. Кроме того, необходимо, чтобы свет обладал достаточно большой степенью когерентности.
Отметим, что можно наблюдать и противоположный эффект – темное пятно в центре картинки при дифракции на открытом отверстии. Такое пятно называется пятном Араго.
31 Зонная пластинка. Закроем все нечетные зоны, оставив открытыми четные (или наоборот). В результате получится пластинка, называемая зонной пластинкой. Из рис. 7.3 видно, что амплитуды поля в точке P будут определяться суммой сонаправленных векторов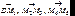 
и т.д. Поэтому осуществляется интерференция волн с усилением. Следовательно, в точке P на оси происходит значительное усиление интенсивности света (примерно в m2 большее, чем дает отверстие в одну зону), т.е. в этой точке свет фокусируется. Зонная пластинка ведет себя как линза. Найдем фокусное расстояние f такой линзы. Будем считать, что лучи падают на зонную пластинку параллельно оси системы, т.е. R = . Тогда точка P является фокусом. Формула (7.5) примет вид:
(7.8)
Следовательно фокусное расстояние равно:
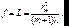(7.9)
Формула такой линзы принимает вид:
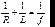(7.10)
В отличие от обычной линзы зонная пластинка имеет несколько фокусов на оси системы в зависимости от количества открытых зон. Отметим, что и расположение зон Френеля на волновом фронте зависит от геометрии рассматриваемой системы.
Интенсивность света в фокусе можно увеличить еще в 4 раза по сравнению с зонной пластинкой, если изменить на фазы вторичных волн, исходящих от всех нечетных (или наоборот – четных) зон. Это можно сделать, например, химическим травлением стеклянной пластинки в нужных местах, чтобы ее толщина там уменьшилась на (n – 1)/2. В этом случае вторичные волны от всех точек волновой поверхности приходят в точку фокуса в одинаковых фазах. Такая дифракционная линза называется линзой Френеля. Трудности метода зон Френеля.Метод зон Френеля приводит к результатам, которые хорошо согласуются с экспериментом для практически важных случаев, когда размеры препятствий много больше длины волны. Однако метод имеет существенные недостатки:
1. Он не решает вопроса о законе ослабления амплитуды вторичных волн в зависимости от направления распространения. Эту зависимость приходится постулировать.
2. Метод Френеля дает неправильную фазу волны. Фаза на фронте волны принимается по определению равной нулю. Поэтому амплитуда волны задается вектором 
(рис.7.3). Вычисленная по методу Френеля амплитуда задается вектором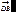 
, т.е. отличается от фактической фазы волны на /2. Хотя для многих практических явлений, зависящих от модуля амплитуды, эта разница в фазах несущественна, она все же с теоретической точки зрения имеет принципиальный характер. Это удается объяснить лишь в более строгой теории дифракции, основанной на интеграле Кирхгофа.
32 Приближение Кирхгофа.
Из теоремы Остроградского–Гаусса
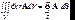(7.11)
положив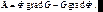 
находим:
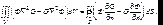(2-я формула Грина) (7.11)
Производные в правой части (7.11) берутся по длине параллельно внешней нормали к замкнутой поверхности S. V – объем, ограниченный поверхностью S. Функции G и Ф вместе со своими первыми и вторыми частными производными непрерывны внутри V и на S .
Рассмотрим монохроматическую волну
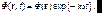(7.12)
Подставляя это выражение в волновое уравнение, получим для пространственно зависящей амплитуды:
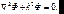(k – волновое число) (7.13)
Пусть объем V ограничен поверхностью S. Точка P0 – фиксированная точка внутри этого объема (начало отсчета), P1 – переменная точка, отличная от P0 и характеризуемая радиус-вектором r01. Функция
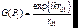(7.14)
удовлетворяет уравнению (7.13) всюду, кроме точки P0 . В P0 функция G обращается в бесконечность, а ее производные терпят разрыв. Значит во всем объеме V формулу Грина применять нельзя. Окружим точку P0 малой сферой S1 (и объемом V1) радиусом с центром в P0 . Вне объема V1 мы имеем право применять формулу Грина. Т.к.
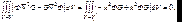(7.15)
то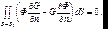 
(7.16)
Отметим, что внешняя нормаль n к S1 направлена внутрь V1 . Из (7.16) получаем:
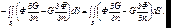(7.17)
Для точек P1 на поверхности S имеем:
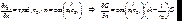(7.18)
Индекс 1 в grad показывает, что grad вычисляется по координатам точки P1 , т.е. grad1 r01 = r01 / r01. Очевидно, что grad0 r01 = r10 / r10 . Отсюда grad1 r01 = – grad0 r01 Для точек P1 на S1 справедливо:
(7.19)
При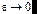 
получаем:
(7.20)
Поэтому из (7.20) и (7.17) имеем:
(7.21)
Это интегральное уравнение называется интегральной теоремой Гельмгольца-Кирхгофаи является основой скалярной теории дифракции. Она позволяет вычислить значение функции Ф в любой точке внутри объема, если известны значения функции и ее производной по нормали на поверхности, ограничивающей этот объем. Для того, чтобы (7.21) использовать не как интегральное уравнение для Ф, а как формулу для вычисления Ф(P0) по известным значениям этой функции и ее производной в точках плоского экрана, Кирхгоф предложил следующие правила для определения их значений в плоскости экрана(приближение Кирхгофа):
1. На отверстиях Ф и Ф/n имеют те же значения, какие они имели бы при отсутствии непрозрачных частей экрана.
2. На непрозрачных частях экрана Ф = 0 и Ф/n = 0.
Выбор граничных условий в соответствии с этими правилами приводит к решению задач дифракции в приближении Кирхгофа. Граничные условия Кирхгофа никогда точно не выполняются, т.к.:
· на краях отверстий должны соблюдаться определенные граничные условия, которые можно найти в соответствии с электромагнитной теорией света;
· за экраном не может быть резкой тени, т.е. скачкообразного обращения Ф в нуль.
Приближение Кирхгофа хорошо работает при линейных размерах отверстий (или экранов) много больших длины волны.
Оптическое приближение.В видимом диапазоне как правило соблюдается условие:
(оптическое приближение) (7.22)
При его выполнении (7.21) принимает вид:
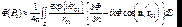(7.23)
33 Формула дифракции Френеля-Кирхгофа.Пусть на отверстие падает сферическая волна, исходящая из точки P2 (рис.7.5):
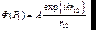(7.24)
Учитывая (7.18) и (7.23), получим в оптическом приближении:
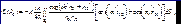(7.25)
где S0 – площадь отверстия. (На непрозрачных частях экрана подынтегральное выражение равно нулю.) (7.25) называется формулой дифракции Френеля-Кирхгофа. Из (7.25) видно, что точечный источник, помещенный в P2 , даст в точке такой же эффект, как и эффект, создаваемый в точке P2 таким же точечным источником, расположенным в P0 (теорема взаимности Гельмгольца).
Вторичные источники. Обозначим:
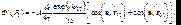(7.26)
Тогда (7.25) примет вид:
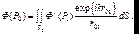(7.27)
Видно, что отличие вторичных источников на отверстии S0от волны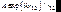 
заключается в следующем:
1. Амплитуда вторичной волны отличается от амплитуды падающей волны множителем k/4
2. Зависимость амплитуды вторичной волны от направления распространения дается множителем 
, который отличается от множителя, предлагавшегося Френелем.
3. Фаза вторичного источника отличается от фазы падающей волны на /2 из-за множителя – i .
Таким образом, в приближении Кирхгофа в рамках электромагнитной теории света удается преодолеть трудности метода зон Френеля.
Приближение Френеля.Пусть дифракционная картина наблюдается в плоскости (плоскости дифракционной картины), параллельной экрану с отверстиями (плоскости источников), l – расстояние между этими плоскостями. В каждой плоскости введем системы координат, как показано на рис.7.6. P0 – точка наблюдения. 
– амплитуда источников.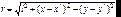 
. Тогда
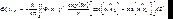(7.28)
Члены с косинусами являются медленно меняющимися функциями по сравнению с быстро осциллирующей экспонентой. Кроме того, углы обычно на практике изменяются в небольших пределах вблизи нуля. Тогда (7.28) с учетом этого приближения упрощается:
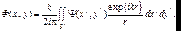(7.29)
При малых углах обычно соблюдаются и следующие неравенства:
(7.30)
Тогда с учетом этого разложим r в ряд по (7.30) и ограничимся квадратичными членами:
(7.31)
где медленно изменяющаяся величина r l в знаменателе вынесена за интеграл, т.к. она на влияет на видность интерференционной картины, а только слабо влияет на общую яркость.
Полученное приближение называется приближением Френеля, а соответствующая ему дифракция – дифракцией Френеля.
34 Дифракция Фраунгофера. Разложим показатель экспоненты в (7.31):
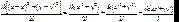. (7.32)
Тогда (7.31) перепишется в виде:
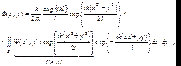(7.33)
Если рассматривать в дальнейшем относительное распределение интенсивности, а не поля в дифракционной картине, то наличие комплексных экспонент перед интегралом можно не учитывать. С другой стороны, если учесть, что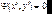 
на непрозрачных частях экрана, то интегрировать можно по координатам от –до +. Поэтому с точностью до множителей функция Ф(x,y) является Фурье–образом функции f(x’,y’) в (7.33) и для изучения дифракционных эффектов можно воспользоваться формализмом преобразований Фурье. При определенных условиях можно перейти и к Фурье–образу от функции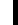 
без экспоненциального множителя. Это можно осуществить при достаточно малых размерах отверстия и при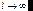 
. Дифракция при этом называется дифракцией Фраунгофера (дифракция в параллельных лучах). Пренебречь экспонентой можно не только при 
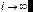, но и при условии, чтобы она не осциллировала (показатель не должен превышать /4, т.е. Re > Im). Т.о., область дифракции Фраунгофера простирается от бесконечности до некоторого минимального значения:
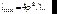(7.34)
где ’ – максимальное расстояние от центра до края отверстия, на котором происходит дифракция. Дифракцию в этой области можно наблюдать на экране без дополнительных устройств. Однако проще наблюдать в фокальной плоскости линзы, расположенной после объекта. Формула (7.33) в области дифракции Фраунгофера принимает вид:
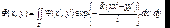. (7.35)
Отметим, что здесь еще необходимо при практических расчетах учесть множитель перед интегралом, определяющий размерность.
35 Дифракция на прямоугольном отверстии (рис.7.7).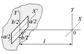 
Отверстие имеет стороны a и b. На отверстии фаза и амплитуда плоской волны постоянна. Комплексная амплитуда волны на отверстии обозначим A0. Тогда, применяя формулу (7.35), получаем для амплитуды поля при дифракции: 
, (7.36)
где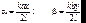 
.
Интенсивность в дифракционной картине с точностью до постоянного множителя имеет вид (см. рис.7.8):
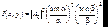. (7.37)
Дифракция на щели.
Рассмотрим падение плоской монохроматической световой волны на бесконечную щель шириной b 
(рис.7.9). Участок dx, находящийся на расстоянии x от левого края щели (начала координат), в направлении Z’ излучает плоскую волну с запаздыванием фазы относительно точки О на kxЧsin. Угол отсчитывается от оси Z – нормали к щели (первоначального направления падающей волны), k – волновое число падающей волны. При записи амплитуды волны учтем, что вся щель в направлении = 0 посылает излучение с амплитудой E0. Предполагая равномерное распределение амплитуды по щели, получим, что участок dx щели пошлет в направлении Z’ волну dE1 с амплитудой E0dx/b :
(7.39)
Отсюда имеем для амплитуды волны от всей щели:
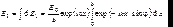(7.40)
После несложного интегрирования и перехода от поля к интенсивности, получаем интенсивность дифракционной картины:
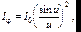(7.41)
где I0 = E02 ; I1 = E12 ;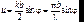 
. (7.42)
Проанализируем выражение (7.41).
1. При = 0 u =0. Используя соотношение 
, получаем, что в центре дифракционной картины интенсивность максимальна и равна I0 .
2. При углах , для которых sinu = 0, а u 0 интенсивность света обращается в нуль. Тогда условие минимума дифракционной картины на одиночной щели принимает вид:
(7.43)
3. Основная часть потока энергии сосредоточена в пределах изменения угла дифракции между первыми (n = 1) симметричными максимумами. График зависимости (7.41) приведен на рис.7.10.
4. Чем меньше (уже) щель, тем шире центральный максимум. Нетрудно заметить, что при b центральный максимум расплывается на всю полуплоскость (/2). Дальнейшее уменьшение щели приводит лишь к монотонному уменьшению интенсивности прошедшего света.
Изучение картины дифракции дает информацию о ширине щели, если известна длина волны используемого света. Наоборот, зная ширину щели, можно найти длину волны. Таким образом, дифракционная картина от данного объекта имеет характерный вид, позволяющий получать информацию о размерах этого объекта. Отмеченное обстоятельство носит достаточно общий характер и лежит в основе метрологического применения дифракционных явлений.
37 Дифракция на круглом отверстии. Пусть R – радиус отверстия. Расчет удобнее вести в полярных координатах (r, ) и (r’, ’) в плоскостях отверстия и дифракционной картины:
(7.44)
Тогда (7.35) для этого случая запишется в виде:
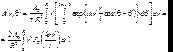(7.45)
где 
– функция Бесселя m-го порядка. Воспользуемся свойством функций Бесселя:
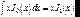. (7.46)
Тогда получаем (рис.7.11):
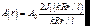. (7.47)
Интенсивность дифракционной картины определяется квадратом этой функции, т.е. в центре картины имеется светлое круглое пятно, окруженное темными и светлыми кольцами. Максимумы интенсивности быстро убывают. Радиусы колец определяются из корней функции Бесселя J1 ()=0. Т.к. существует приближенное соотношение 
, то качественно распределение интенсивности выглядит примерно так же, как и на рис.7.10. Угловой размер центрального светлого пятна (диска Эйри), наблюдаемого из центра круглого отверстия, равен:
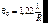. (7.48)
38 Дифракционная решетка. Прозрачная (амплитудная) дифракционная 
решетка представляет собой правильную плоскую структуру из большого количества параллельных щелей с шириной каждой щели b и расстоянием d между соседними щелями. Расстояние d чаще называют периодомили постоянной дифракционной решетки (рис.7.12). Пусть на 
эту решетку нормально падает плоская монохроматическая волна. Найдем интенсивность света I в дифракционной картине.
Методика расчета и система обозначений та же, что и для одиночной щели. От элемента dx какой-то n-й щели в исследуемом направлении распространяется волна вида:
(7.49)
Вся n-я щель пошлет волну вида:
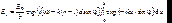(7.50)
Для учета действия всех щелей по принципу суперпозиции можно сложить все образовавшиеся напряженности поля:
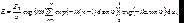(7.51)
где N – полное число щелей, участвующих в дифракции. Множитель с интегралом был посчитан выше для случая одной щели. Он не зависит от n и может быть вынесен за знак суммы. Введем обозначение:
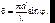(7.52)
Сумма в (7.51) представляет собой сумму N членов геометрической прогрессии. Тогда (7.51) перепишется в виде:
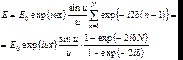(7.53)
Интенсивность света в дифракционной картине получается умножением (7.53) на комплексно сопряженную величину I=EE* :
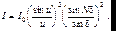(7.54)
Множитель (sinu/u)2 характеризует распределение интенсивности в результате дифракции плоской волны на каждой щели и является огибающей всей дифракционной картины, а множитель (sinN/sin)2 учитывает интерференцию между волнами, исходящими от всех щелей. Множитель I0 определяет интенсивность света, излучаемого в направлении = 0, которая зависит от потока энергии, падающего на решетку света. Вид дифракционной картины показан на рис.7.13.
Величина dsinравна разности хода между волнами, испускаемыми двумя эквивалентными точками соседних щелей. Условие главных максимумов для дифракционной решетки определяется формулой:
(7.55)
А условие (7.43) определяет положение минимумов огибающей. Наклонное падение света на дифракционную решетку. Пусть параллельный пучок света падает на дифракционную решетку под углом (рис.7.14). Как и прежде дифракционные максимумы будут 
наблюдаться при разности хода волн, идущих от одинаковых точек соседних щелей, равной целому числу длин волн:
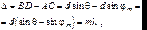(7.56)
где m – направление на m-й максимум. При 
, как правило, углы дифракции малы, поэтому
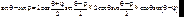. (7.57)
Обозначив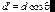 
, а 
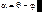, получаем условие максимума
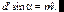. (7.58)
Т.е., при наклонном падении света на решетку, если вести отсчет углов о падающих лучей, роль периода решетки играет проекция периода решетки на перпендикулярное падающему пуску направление. Это позволяет использовать решетки с большим периодом для дифракции с очень короткой длиной. Дифракция света на решетке с гармоническим пропусканием. Рассмотрим дифракцию Фраунгофера на решетке, коэффициент пропускания которой не дискретен, а изменяется по гармоническому закону:
. (7.59)
Найдем только угловое распределение максимумов в этом случае. Поэтому будем считать, что размеры решетки бесконечны. Тогда распределение поля на выходе решетки определяется формулой
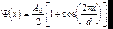. (7.60)
Подставив (7.60) в формулу (7.35) для дифракции Фраунгофера, получаем:
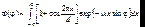(7.61)
Определив косинус через мнимую экспоненту, имеем:
(7.62)
где C – некоторая константа, включающая амплитуду падающей на решетку волны. Интегралы в (7.62) легко вычисляются через –функции:
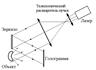
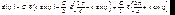. (7.63)
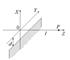Отсюда видно, что в отличие от обычной решетки при дифракции на гармонической структуре наблюдаются лишь три главных дифракционных максимума с порядками 
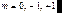. Этому процессу можно сопоставить математическое разложение функции пропускания (7.59) в ряд Фурье, содержащий лишь три члена с соответствующими пространственными частотами (волновыми числами), т.к., как указывалось выше, дифракционное устройство физически приближенно осуществляет преобразование Фурье. В случае более сложной функции пропускания (например, как для классической щелевой решетки либо структуры с произвольной функцией пропускания) ее разложение в ряд (или интеграл) Фурье содержит высшие гармоники, которые и определяют пространственное распределение спектра достаточно большого количества дифракционных максимумов. Отметим, что полученные выводы нам понадобятся при рассмотрении основ голографии.
Дифракция на прямолинейном крае экрана. (рис.7.15) Ограничимся случаем падения плоской волны. Основной интерес представляет распределение интенсивности вблизи края геометрической тени, т.е. d << l. Тогда из (7.35) получаем:
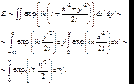(7.64)
где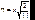 
. Последнее выражение в (7.64) представляет собой параметрическое уравнение спирали Корню (клотоиды) (рис.7.16), позволяющей графически определить вид дифракционной картины от полубесконечного экрана. Функции, отложенные на рис. 7.16 по декартовым осям, называются интеграламиФренеля:
. (7.65)
Параметр есть длина дуги спирали Корню, отсчитываемая от точки 0. Распределение интенсивности вблизи края геометрической тени показано на рис.7.17.
39 Разрешающая способность дифракционной решетки. Для количественной оценки разрешающей способности дифракционных спектральных приборов служит критерий Рэлея: две спектральные линии являются разрешенными, если максимум дифракционной картины для одной длины волны совпадает с ближайшим минимумом для другой длины волны. Вспомним, что для интерферометра Фабри-Перо мы воспользовались близким следствием из критерия Рэлея – пересечением двух соседних максимумов в интерференционной картине на полувысоте. Часто пользуются еще одним следствием из критерия Рэлея – при равной интенсивности исследуемых симметричных максимумов глубина провала между «горбами» составляет 20% от максимума. Конечно, эти следствия, как, впрочем, и сам критерий Рэлея являются достаточно условными. Но они позволяют вполне объективно оценить границу разрешения данного спектрального прибора.
Найдем разрешающую способность дифракционной решетки исходя из критерия Рэлея. Между главными максимумами дифракционной картины располагаются N – 1 минимум, где N – общее число щелей, участвующее в дифракции. Тогда критерий Рэлея запишется в виде:
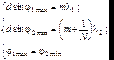(7.66)
Тогда разрешающая способность дифракционной решетки равна: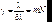 
. (7.67)
Переход от интерференции двух волн к многолучевой интерференции приводит к концентрации излучения вблизи определенных направлений и к увеличению темных промежутков между максимумами, т.е. к увеличению разрешающей способности.
Дисперсионная область дифракционной решетки ищется точно так же, как и для интерферометра Фабри-Перо, т.е. по формуле (6.46):
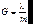. (7.68)
Сравнение характеристик спектральных аппаратов. Высокая разрешающая способность в спектральных приборах типа ИФП (~106) и дифракционной решетки (~105) достигается за счет различных факторов. В ИФП – за счет высоких порядков интерференции (из-за достаточно большой базы интерферометра) при сравнительно небольшом числе интерферирующих волн (нескольких десятков). В дифракционной решетке все наоборот – высокая разрешающая способность достигается за счет большого числа интерферирующих волн при малом порядке интерференции. С другой стороны, порядок интерференции (см. (6.46) и (7.68)) определяет малое значение дисперсионной области для ИФП (~10-2 нм) и большое его значение для дифракционной решетки (~103 нм). Поэтому для получения оптимальных характеристик в эксперименте используют комбинацию различных спектральных приборов. Недостатком дифракционной решетки является малая интенсивность выходного сигнала. ИФП лишен этого недостатка.
40 Голографией называют метод записи и последующего восстановления пространственной структуры световых волн, основанный на явлениях интерференции и дифракции когерентных пучков света. Как и фотография, она обеспечивает возможность записи, хранения и воспроизведения зрительных образов предметов. Фотопластинка, на которой записана эта информация, называется голограммой. В отличие от фотографии голография позволяет записать и восстановить не двухмерное распределение освещенности в плоскости снимка, а рассеянные предметом световые волны со всеми их характеристиками – направлением распространения,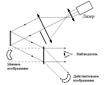 
амплитудой, фазой, длиной волны. Восстановленные голограммой световые волны создают полную иллюзию реальности наблюдаемых предметов.
На голограмме регистрируется не оптическое изображение объекта, а интерференционная картина, возникающая при наложении световой волны, рассеянной объектом (предметной волны), и когерентной с ней опорной (или референтной) волны.
Рассмотрим двухлучевую схему голографии (рис.8.1). Исследуемый объект освещают расширенным с помощью телескопа пучком света лазера. Рассеянная объектом световая волна, а также опорная, отраженная от зеркала, попадают на фотопластинку, на которой регистрируется возникающая интерференционная картина. Дальше пластинка проявляется обычным способом. Получающуюся на голограмме упорядоченную интерференционную структуру можно рассмотреть только с помощью микроскопа.
Для восстановления волны убирают исследуемый объект и помещают голограмму на то место, где находилась фотопластинка (рис.8.2). Освещая ее светом однотипного лазера, наблюдают через голограмму изображение объекта, которое получается там же, где находился объект. Наблюдатель видит «мнимое» изображение предмета как сквозь дымчатое стекло. Причем, т.к. в голограмме зафиксирована вся информация о предмете, то объект воспринимается объемно. Кроме «мнимого», есть и «действительное изображение», имеющее обратный рельеф наблюдаемой поверхности.
Пусть требуется зарегистрировать плоский волновой фронт с волновым вектором k1 , нормальным к оси X и направленным под углом к оси Z (рис.2). Поместим в плоскость XOY фотопластинку. В этой плоскости распределение поля имеет вид:
(8.1)
Если зафиксировать на фотопластинке соответствующую (8.1) интенсивность, то мы получим обычное фотографическое «изображение» плоской волны – пластинка будет равномерно засвечена. Сохранить же информацию о фазе волны позволяет добавление опорной волны. Пусть плоская опорная волна E2направлена вдоль Z. Тогда распределение интенсивности на пластинке примет вид:
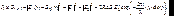(8.2)
Распределение интенсивности представляет собой периодическую систему полос, параллельных оси X с пространственным периодом /sin. После проявки фотопластинки получается плоская дифракционная решетка с синусоидальным законом амплитудного пропускания (правда, если амплитудное пропускание линейно связано с освещенностью фотопластинки). Это и есть голограмма исходной плоской волны. Освещение такой решетки плоской волной, тождественной опорной волне, приводит к появлению двух дифрагированных плоских волн по углами 1 к оси Z (т.е. дифракционных максимумов) (см. гл.7):
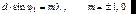(8.3)
Т.о., освещение тонкослойной голограммы только опорной волной приводит к появлению как предметной, так и паразитной волны, симметричной исходной. Ее возникновение связано с тем, что на обычной голограмме не фиксируется направление записываемой волны: голограмма не изменится, если эта волна распространяется в противоположном направлении. Рассматриваемые далее толстослойные голограммы этим недостатком не обладают.
Аналогично можно вместо плоской волны рассмотреть получение голограммы сферической волны. В этом случае при плоском опорном фронте мы получим голограмму в виде синусоидальной зонной пластинки, которая при облучении плоской волной дает изображение точки – источника сферической волны. Другими словами, зонная пластинка является голограммой точки. Разбивая произвольный объект на совокупность независимых точечных источников, для каждого из которых справедливы эти рассуждения, мы приходим к описанию голограммы произвольного поля через наложение множества зонных пластинок Френеля.
Отметим, что каждый участок голограммы способен восстановить изображение всего объекта, но качество изображения при уменьшении площади голограммы ухудшается.
До сих пор мы рассматривали способ записи и воспроизведения так называемых тонкослойных голограмм. В 1962 г. советский ученый Ю.Н. Денисюк осуществил метод записи и воспроизведения голограммы в трехмерной среде. В этом методе используются толстослойные (порядка нескольких десятков микрометров) фотопластинки. Схема записи такой голограммы при встречных пучках (опорной и предметной волны) за счет образования в толще фотоэмульсии стоячей волны показана на рис.8.3. После экспозиции при облучении монохроматическим светом в результате дальнейшей химической обработки в фотоэмульсии получается трехмерная дифракционная решетка с полупрозрачными отражающими слоями серебра (так называемыми слоями Липпмана). Если затем полученную голограмму осветить опорной волной, то частично отраженные от слоев Липпмана когерентные световые волны, интерферируя, дадут изображение предмета в исходном положении. Интерференционное усиление происходит в том случае, когда отраженные от слоев волны синфазны, т.е. удовлетворяют так называемому условию Вульфа-Брэгга:
, (8.4)
где d – расстояние между слоями Липпмана, – угол скольжения отраженной брэгговской волны, m – целые числа.
Выполнение этого условия приводит к избирательности голограммы по отношению к длине восстанавливающей опорной волны. Т.к. трехмерная решетка пропустит (точнее, отразит) излучение только той длины волны монохроматического света, под действием которого она записывалась (то же самое можно отметить и о направлении ), то можно восстанавливать изображение, используя источник сплошного спектра. Если исходные опорная и предметная волны содержали несколько длин волн, то с фотоэмульсии возникнет несколько пространственных решеток. При освещении таким образом записанной голограммы источником сплошного света (например, солнечного или от лампы накаливания) можно получить объемное цветное изображение.
Основные области применения голографии:
1. Запись и хранение информации, в т.ч. и визуальной (оптическая голографическая память). На голографическую пластинку размером 3232 мм2 можно записать 1024 голограммы, каждая по 1 мм2 и содержит, например, одну страницу текста. В толстослойной голограмме можно производить независимую запись и аналогично восстановление, изменяя угол падения опорной волны. В зависимости от типа записывающей среды память может быть как постоянной, так и стираемой. В тонких оптических средах могут быть записаны примерно 108 бит/см2, а при использовании объемной голографии теоретически можно запомнить примерно до 1010 бит/см3. Сюда же можно отнести и всевозможные художественные применения голографии (объемные изображения музейных предметов, голографическое кино, объемные портреты и т.д.)
2. Оптическая обработка информации и системы распознавания образов (распознавание знаков, языка, отпечатков пальцев, изображений). Сравнение объекта (например, корреляционным методом) ведется с записанными голограммами известных объектов. Корректировка и обработка изображений может быть проведена с помощью определенных голографических фильтров.
3. Голографическая интерферометрия. Этот метод позволяет исследовать изменения (например, деформацию), происшедшие в наблюдаемом объекте под каким-либо внешним воздействием. В основе регистрации таких малых деформаций лежит явление интерференции двух волн, существовавших в разные моменты времени и записанных на одну голограмму. По полученной полосатой интерференционной картине можно определить изменения до десятых долей микрометра. С помощью голографической интерферометрии возможно измерение всех видов деформации прозрачных и непрозрачных тел; очень малых перемещений; типов колебаний; распределений температуры; произвольных распределений неоднородностей. Этот метод на практике применяют для исследований частей машин; деталей кузова автомобилей; автомобильных шин и других легко деформируемых тел; оптических элементов; музыкальных инструментов; распределения неоднородностей в атмосфере и других средах; плазмы.
41 Описание анизотропных сред. Оптической анизотропией называется зависимость оптических свойств среды от направления распространения света в ней. Физическая природа анизотропии вещества связана с особенностями строения его молекул или особенностями кристаллической решетки, в узлах которой находятся атомы или ионы. Взаимодействие света с веществом для анизотропных сред не может быть моделировано колебаниями одного осциллятора. Для описания таких сред необходимо ввести три различных взаимно перпендикулярных осциллятора и характеризовать три взаимно перпендикулярных направления различными значениями показателя преломления. Однако изучение распространения света в анизотропных средах мы будем строить не на учете атомной структуры среды, а с помощью феноменологической электромагнитной теории. В рамках этой теории анизотропия учитывается тем, что в материальном уравнении диэлектрическая восприимчивость () представляет собой тензор, а не скаляр, как для изотропной среды. Анизотропию магнитных свойств сред мы рассматривать не будем, т.к., во-первых, принцип описания будет точно таким же, и, во-вторых, магнитная анизотропия используется значительно реже.
В анизотропной среде проекции поляризованности связаны с проекциями напряженности электрического поля соотношениями:
(9.1)
В дальнейшем для простоты будем нумеровать декартовы оси координати соответствующие им проекции числами или индексами 1, 2, 3. Матрица величин ij называется тензором диэлектрической восприимчивости. Тогда систему (9.1) можно записать в компактном виде: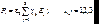 
(9.2)
Соотношение между компонентами вектора электрического смещения D и поляризованностью P для анизотропной среды принимает вид:
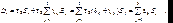(9.3)
где ij – символ Кронекера. Тензор ij :
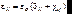(9.4)
называется тензором диэлектрической проницаемости.
Рассмотрим основные его свойства. Запишем выражение для плотности электрической энергии w с учетом (9.3):
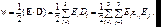(9.5)
Изменим порядок индексов в (9.5):
(9.6)
Вычитая почленно (9.6) из (9.5), получим:
(9.7)
Отсюда следует, что т.к. проекции поля E независимы, то тензор диэлектрической проницаемости является симметричным: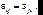 
(9.8)
Воспользуемся математическими свойствами полученных выражений. Т.к. плотность электрической энергии положительна, то стоящая в правой части (9.5) квадратичная форма является положительно определенной.
Замечание.
Формой степени n (или однородным многочленом) называется многочлен от нескольких переменных, каждый член которого имеет степень n относительно совокупности всех переменных.
Действительную квадратичную форму f(x1, x2, ... xn=ееaijxixj называют положительно определенной, если f > 0 для любого набора значений переменных x1, x2, ..., xn , среди которых есть хотя бы одно, отличное от нуля.
Перейдя к новым переменным:
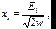(9.9)
выражение (9.5) можно записать в виде:
(9.10)
Как известно из математики, с помощью преобразования системы координат такая форма может быть приведена к виду:
(9.11)
Полученные таким образом оси X, Y, Zновой системы координат называют главными осями тензора диэлектрической проницаемости (в дальнейшем мы их так и будем обозначать большими буквами). В главной системе координат тензор диэлектрической проницаемости является диагональным:
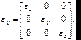(9.12)
Уравнение (9.11) описывает эллипсоид с полуосями, расположенными вдоль главных осей тензора и равными x-1/2, y-1/2, z-1/2. В главных осях соотношение (9.3) примет вид:
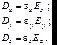(9.13)
Т.к. в общем случае элементы тензора диэлектрической проницаемости неодинаковы, то в анизотропной среде векторы D и E не коллинеарны.
42 Распространение плоской электромагнитной волны в анизотропной среде.Подставляя векторы E,D,H, B в плоской ЭМВ в виде
(9.14)
в уравнения Максвелла (2.1) — (2.6), получим следующие соотношения между векторами полей и волновым вектором k :
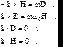(9.15)
Волновой вектор k показывает направление распространение волнового фронта, т.е. фазовая скорость v направлена вдоль волнового вектора. Введем единичный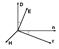 
вектор направления распространения волны n: 
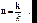(9.16)
Поток энергии, по определению, распространяется по направлению вектора Пойнтинга S = EH. Направление потока энергии в волне называется лучом. Т.к. энергия ЭМВ распространяется с групповой скоростью, то групповая скорость u направлена вдоль луча. Введем единичный вектор в направлении распространения луча:
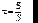(9.17)
Т.к. а анизотропной среде векторы Eи Dне коллинеарны, то направления распространения волны и луча не совпадают. Соответственно не совпадают по направлению гр