Главная | Обратная связь

Движение газа и звёзд

Так как звёзды расположены далеко друг от друга и вероятность их столкновения мала, звёзды, как в галактиках, так и в скоплениях, представляют собой бесстолкновительную среду. Это легко показать. Будем называть столкновением двух звёзд случай, когда две звезды при сближении под действием силы гравитации изменят направление движения, сохранив при этом полную энергию. Тогда рассмотрим это сближение относительно центра масс звёзд. Для упрощения расчётов будем считать, что массы звёзд равны, и их скорости на начало сближения (формально на бесконечно большом расстоянии) тоже. Для первой оценки это вполне допустимое приближение. Запишем закон сохранения механической энергии:

,

где V — текущая скорость звёзд (скорости должны быть одинаковы из-за соображений симметрии), r — расстояние между звёздами, V₀ — скорость на бесконечности до взаимодействия, а G — гравитационная постоянная. Будем считать, что звёзды испытали столкновение, если в момент их сближения кинетическая энергия удвоилась. Тогда, подставив значение прицельного параметра d в уравнение, написанное выше, получим:

.

Тогда диаметр сечения столкновения тел и, соответственно, площадь сечения взаимодействия равны:

,

.

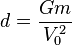Оценим характерное время столкновения для звёзд окрестностей Солнца (n = 3·10⁻⁵⁶ см⁻³, а относительная скорость движения 20 км/с). Получим:

.

Полученное время больше времени жизни Вселенной на три порядка. И даже в звёздных скоплениях, где концентрация звёзд на три порядка больше, ситуация не улучшается. Заметим, что можно было бы провести более точный расчёт, с учётом закона сохранения импульса и т. д., но результаты получились бы схожими. Из бесстолкновительности среды напрашивается вывод о неравновесности системы и распределении случайных скоростей звёзд не максвелловским образом. Характерное время его установления должно быть много большим времени свободного пробега звезды. Однако в действительности всё оказалось гораздо сложнее.

Измерения показали, что звёзды, за исключением самых молодых, представляют собой частично «прорелаксировавшую» систему: распределение случайных скоростей звёзд максвелловское, но с различными дисперсиями по различным осям. Более того, в одном и том же объёме пространства наблюдается систематический, хотя и замедляющийся, рост случайных скоростей для старых звёзд. Таким образом, можно утверждать, что звёздный диск со временем нагревается.

Данная проблема не решена окончательно, по-видимому, решающую роль играют всё же столкновения, но не со звёздами, а с массивными газовыми облаками.