Главная | Обратная связь

Математическое описание стоячих волн

В одномерном случае две волны одинаковой частоты, длины волны и амплитуды, распространяющиеся в противоположных направлениях (например, навстречу друг другу), будут взаимодействовать, в результате чего может возникнуть стоячая волна. Например, гармоничная волна, распространяясь вправо, достигая конца струны, производит стоячую волну. Волна, что отражается от конца, должна иметь такую ​​же амплитуду и частоту, как и падающая волна.

Рассмотрим падающую и отраженную волны в виде:

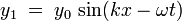
где:

· y₀ — амплитуда волны,

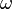· — циклическая (угловая) частота, измеряемая в радианах в секунду,

· k — волновой вектор, измеряется в радианах на метр, и рассчитывается как 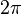поделённое на длину волны ,

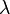· x и t — переменные для обозначения длины и времени.

Поэтому результирующее уравнение для стоячей волны y будет в виде суммы y₁ и y₂:

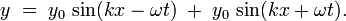
Используя тригонометрические соотношения, это уравнение можно переписать в виде:

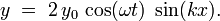
Если рассматривать моды 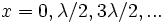и антимоды 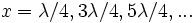, то расстояние между соседними модами / антимодами будет равно половине длины волны .

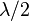Волновое уравнение

Для того, чтобы получить стоячие волны как результат решения однородного дифференциального волнового уравнения (Даламбера)

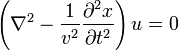
необходимо соответствующим образом задать его граничные условия (например, закрепить концы струны).

В общем случае неоднородного дифференциального уравнения

,

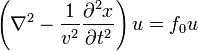где 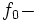выполняет роль «силы», с помощью которой осуществляется смещение в определенной точке струны, стоячая волна возникает автоматически

 

28.Термодинамическая система — это некая физическая система, состоящая из большого количества частиц, способная обмениваться с окружающей средой энергией и веществом. Также обычно полагается, что такая система подчиняется статистическим закономерностям. Для термодинамических систем справедливы законы термодинамики.

Для описания термодинамической системы вводят так называемые термодинамические величины — набор физических величин, значения которых определяют термодинамическое состояние системы. Примерами термодинамических величин являются:

· температура

· давление

· объём

· внутренняя энергия

· энтропия

· энтальпия

· свободная энергия Гельмгольца

· энергия Гиббса

Если термодинамическое состояние системы не меняется со временем, то говорят, что система находится в состоянии равновесия. Строго говоря, термодинамические величины, приведённые выше, могут быть определены только в состоянии термодинамического равновесия.

Внутреннюю энергию тела нельзя измерить напрямую. Можно определить только изменение внутренней энергии:

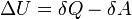
где

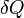· — подведённое к телу количество теплоты, измеренное в джоулях

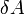· ^[1] — работа, совершаемая телом против внешних сил, измеренная в джоулях

Эта формула является математическим выражением первого начала термодинамики

Для квазистатических процессов выполняется следующее соотношение:

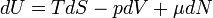
где

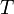· — температура, измеренная в кельвинах

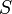· — энтропия, измеренная в джоулях/кельвин

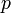· — давление, измеренное в паскалях

· — химический потенциал

· — количество частиц в системе

 

Понятие энтропии впервые было введено Клаузиусом в термодинамике в 1865 году для определения меры необратимого рассеивания энергии, меры отклонения реального процесса от идеального. Определённая как сумма приведённых теплот, она является функцией состояния и остаётся постоянной при обратимых процессах, тогда как в необратимых — её изменение всегда положительно.

,

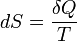где 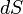— приращение энтропии; 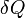— минимальная теплота, подведенная к системе; T — абсолютная температура процесса;

Свобо́дная эне́ргия Гельмго́льца (или просто свобо́дная эне́ргия) — термодинамический потенциал, убыль которого в квазистатическом изотермическом процессе равна работе, совершённой системой над внешними телами.

Свободная энергия Гельмгольца для системы с постоянным числом частиц определяется так:

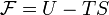· , где 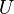— внутренняя энергия, 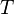— абсолютная температура, 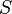— энтропия.

 

Свободная энергия Гиббса (или просто энергия Гиббса, или потенциал Гиббса, или термодинамический потенциал в узком смысле) — это величина, показывающая изменение энергии в ходе химической реакции и дающая таким образом ответ на вопрос о принципиальной возможности протекания химической реакции; это термодинамический потенциал следующего вида:

где 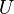— внутренняя энергия, 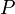— давление, 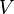— объём, 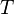— абсолютная температура, 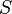— энтропия.