 |
|
Цепь с активным сопротивлением, индуктивностью и емкостью
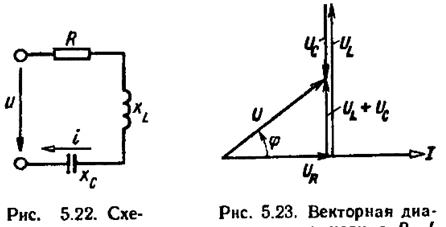 |
Цепь с активным сопротивлением, индуктивностью и емкостью представляет собой общий случай последовательного соединения активных и реактивных сопротивлений и является последовательным колебательным контуром (рис. 5.12).
Рисунок 5.12 Схема цепи переменного тока с R, L и C и векторная диаграмма
Принимаем фазу тока нулевой: 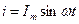 .
.
Тогда напряжение на активном сопротивлении  , напряжение на индуктивности
, напряжение на индуктивности 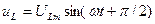 , напряжение на емкости
, напряжение на емкости 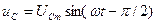 . Построим векторную диаграмму при условии
. Построим векторную диаграмму при условии 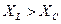 , т. е.
, т. е. 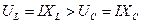 .
.
Вектор результирующего напряжения U замыкает многоугольник векторов 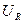 ,
,  и
и 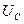 (рис. 5.12). Вектор
(рис. 5.12). Вектор 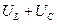 определяет напряжение на индуктивности и емкости. Как видно из диаграммы, это напряжение может быть меньше напряжения на каждом из участков в отдельности. Это объясняется процессом обмена энергией между индуктивностью и емкостью. Выведем закон Ома для рассматриваемой цепи. Так как модуль вектора
определяет напряжение на индуктивности и емкости. Как видно из диаграммы, это напряжение может быть меньше напряжения на каждом из участков в отдельности. Это объясняется процессом обмена энергией между индуктивностью и емкостью. Выведем закон Ома для рассматриваемой цепи. Так как модуль вектора 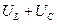 рассчитывают как разность действующих значений
рассчитывают как разность действующих значений 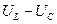 , то из диаграммы рис. 5.12 следует, что
, то из диаграммы рис. 5.12 следует, что  . Но
. Но 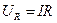 ,
, 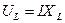 ,
, 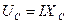 ; следовательно,
; следовательно, 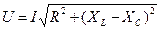 , откуда
, откуда
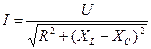 (5.27)
(5.27)
Введя обозначение 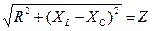 , где Z – полное сопротивление цепи, найдем
, где Z – полное сопротивление цепи, найдем
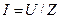 (5.28)
(5.28)
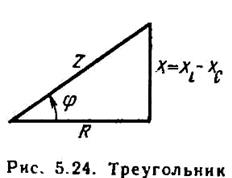
Разность между индуктивным и емкостным сопротивлениями 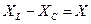 называют реактивным сопротивлением цепи. Учитывая это, получим треугольник сопротивлений для цепи с R, L и С (рис. 5.13). При
называют реактивным сопротивлением цепи. Учитывая это, получим треугольник сопротивлений для цепи с R, L и С (рис. 5.13). При 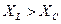 реактивное сопротивление положительно и сопротивление цепи носит активно-индуктивный характер. При
реактивное сопротивление положительно и сопротивление цепи носит активно-индуктивный характер. При 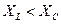 реактивное сопротивление отрицательно и сопротивление цепи носит активно-емкостный характер. Знак сдвига фаз между током и напряжением получим автоматически, так как реактивное сопротивление — величина алгебраическая:
реактивное сопротивление отрицательно и сопротивление цепи носит активно-емкостный характер. Знак сдвига фаз между током и напряжением получим автоматически, так как реактивное сопротивление — величина алгебраическая:
 |
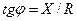 (5.29)
(5.29)
Рисунок 5.13 Треугольник сопротивлений для цепи с R, L и C
Таким образом, при 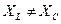 преобладает или индуктивное, или емкостное сопротивление, т. е. с энергетической точки зрения цепь с R, L и С сводится к цепи с R, L или с R, С. Тогда мгновенная мощность
преобладает или индуктивное, или емкостное сопротивление, т. е. с энергетической точки зрения цепь с R, L и С сводится к цепи с R, L или с R, С. Тогда мгновенная мощность
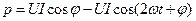
причем знак φ определяется по формуле (5.29). Соответственно активная, реактивная и полная мощности характеризуются выражениями 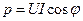 ;
;  ;
; 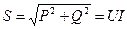 .
.