Главная | Обратная связь

Цепь с индуктивностью

Под действием синусоидального напряжения в цепи с индуктивной катушкой без ферромагнитного сердечника (рис. 5.3) проходит синусоидальный ток 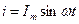. В результате этого вокруг катушки возникает переменное магнитное поле и в катушке и наводится ЭДС самоиндукции. При R=0 напряжение источника целиком идет иа уравновешивание этой ЭДС; следовательно, . Так как , то

(5.5)

или

где

(5.6)

Рисунок 5.3 Схема цепи переменного тока с индуктивностью и временные диаграммы напряжения, тока и ЭДС

 

Сопоставляя выражения для мгновенных значения тока и напряжения, приходим к выводу, что ток в цепи с индуктивностью отстает по фазе от напряжения на угол π/2. Физически это объясняется тем, что индуктивная катушка реализует инерцию электромагнитных процессов. Индуктивность катушки L является количественной мерой этой инерции. Фазовые соотношения между током, напряжением и ЭДС для цепи с индуктивностью показаны на рис. 5.3 и 5.4.

Рисунок 5.4 Векторная диаграмма напряжения, тока и ЭДС для цепи с индуктивностью

 

Выведем закон Ома для этой цепи. Из выражения (5.6) следует, что . Пусть 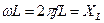, где — индуктивное сопротивление цепи. Тогда получим выражение

, (5.7)

которое является законом Ома для амплитудных значений. Разделив левую и правую части этого выражения на , получим закон Ома для действующих значений:

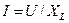(5.8)

Проанализируем выражение для . С увеличением частоты тока f индуктивное сопротивление увеличивается (рис. 5.5). Физически это объясняется тем, что возрастает скорость изменения тока, а следовательно, и ЭДС самоиндукции.

Рисунок 5.5 Зависимость индуктивного сопротивления X_L от частоты f

 

Рассмотрим энергетические характеристики цепи с индуктивностью.

Мгновенная мощность. Как и для цепи с R, мгновенное значение мощности определяется произведением мгновенных значений напряжения и тока: .

Так как и , то окончательно имеем

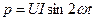(5.9)

Из графика рис. 5.6 видно, что при одинаковых знаках напряжения и тока мгновенная мощность положительна, а при разных знаках — отрицательна. Физически это означает, что в первую четверть периода переменного тока энергия источника преобразуется в энергию магнитного поля катушки. Во вторую четверть периода, когда ток убывает, катушка возвращает накопленную энергию источнику. В следующую четверть периода процесс передачи энергии источником повторяется и т. д.

Таким образом, в среднем катушка не потребляет энергии и, следовательно, активная мощность Р = 0.

Реактивная мощность. Для количественной характеристики интенсивности обмена энергией между источником и катушкой служит реактивная мощность:

(5.10)

Единицей реактивной мощности является вольт-ампер реактивный (ВАр).

 

Рисунок 5.6 Временные диаграммы напряжения, тока и мгновенной мощности для цепи с индуктивностью