 |
|
Цепь с активным сопротивлением и индуктивностью
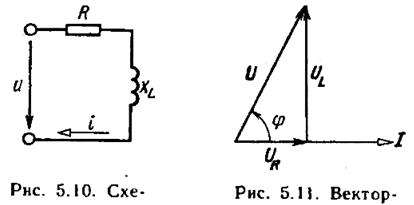 |
Цепь (рис. 5.7) состоит из участков, свойства которых известны. Проанализируем работу данной цепи. Пусть ток в цепи изменяется по закону
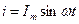 . Тогда напряжение на активном сопротивлении
. Тогда напряжение на активном сопротивлении  , так как на этом участке напряжение и ток совпадают по фазе. Напряжение на катушке
, так как на этом участке напряжение и ток совпадают по фазе. Напряжение на катушке 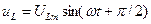 , поскольку на индуктивности напряжение опережает по фазе ток на угол π/2. Построим векторную диаграмму для рассматриваемой цепи (рис. 5.7).
, поскольку на индуктивности напряжение опережает по фазе ток на угол π/2. Построим векторную диаграмму для рассматриваемой цепи (рис. 5.7).
Рисунок 5.7 Схема цепи переменного тока с R и L и векторная диаграмма
Сначала откладываем вектор тока I, затем вектор напряжения UR, совпадающий по фазе с вектором тока. Начало вектора  , опережающего вектор тока на угол π /2, соединим с концом вектора
, опережающего вектор тока на угол π /2, соединим с концом вектора 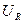 для удобства их сложения. Суммарное напряжение
для удобства их сложения. Суммарное напряжение 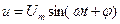 изображается вектором U, сдвинутым по фазе относительно вектора тока на угол φ. Векторы
изображается вектором U, сдвинутым по фазе относительно вектора тока на угол φ. Векторы 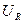 ,
,  и U образуют треугольник напряжений. Выведем закон Ома для этой цепи. На основании теоремы Пифагора для треугольника напряжений имеем
и U образуют треугольник напряжений. Выведем закон Ома для этой цепи. На основании теоремы Пифагора для треугольника напряжений имеем 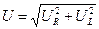 . Но
. Но 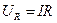 a;
a;  следовательно,
следовательно, 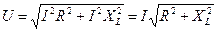 , откуда
, откуда
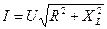 (5.11)
(5.11)
Введем обозначение 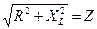 , где Z — полное сопротивление цепи. Тогда выражение закона Ома примет вид
, где Z — полное сопротивление цепи. Тогда выражение закона Ома примет вид
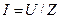 (5.12)
(5.12)
Так как полное сопротивление цепи Z определяется по теореме Пифагора, ему соответствует треугольник сопротивлений (рис. 5.8). Поскольку при последовательном соединении напряжения на участках прямо пропорциональны сопротивлениям, треугольник сопротивлений подобен треугольнику напряжений. Сдвиг фаз φ между током и напряжением определяется из треугольника сопротивлений:
 (5.13)
(5.13)
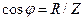 (5.14)
(5.14)
Для последовательной цепи условимся отсчитывать угол φ от вектора тока I. Поскольку вектор U сдвинут по фазе относительно вектора I на угол φ против часовой стрелки, этот угол имеет положительное значение. В дальнейшем покажем, что знак угла φ определяется по формальному признаку.
 |
Выведем энергетические соотношения для цепи с активным сопротивлением и индуктивностью.
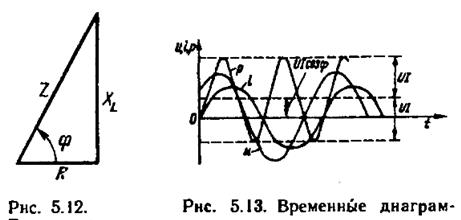
Рисунок 5.8 Треугольник сопротивлений для цепи с R и L и временные диаграммы напряжения, тока и мгновенной мощности
Мгновенная мощность. Мгновенная мощность выражается соотношениями
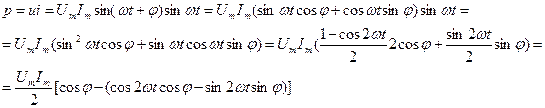
Или
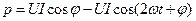 (5.15)
(5.15)
Анализ выражения (5.15) и рис. 5.8, построенного на его основе, показывает, что мгновенное значение мощности колеблется около постоянного уровня 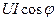 , который характеризует среднюю мощность. Отрицательная часть графика определяет энергию, которая переходит от источника к индуктивной катушке и обратно.
, который характеризует среднюю мощность. Отрицательная часть графика определяет энергию, которая переходит от источника к индуктивной катушке и обратно.
Средняя мощность. Средняя, или активная, мощность для данной цепи характеризует расход энергии на активном сопротивлении и, следовательно, 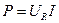 . Из векторной диаграммы (см. рис. 5.4) видно, что
. Из векторной диаграммы (см. рис. 5.4) видно, что 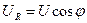 . Тогда
. Тогда
 (5.16)
(5.16)
Реактивная мощность. Реактивная мощность характеризует интенсивность обмена энергией между индуктивной катушкой и источником:
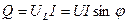 (5.17)
(5.17)
Полная мощность. Понятие полной мощности применяют для оценки предельной мощности электрических машин:
 . (5.18)
. (5.18)
Так как  , то
, то
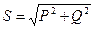 . (5.19)
. (5.19)
Единицей полной мощности является вольт-ампер (В-А).
Цепь с емкостью
Проанализируем процессы в цепи, представленной на рис. 5.9.
Зададимся напряжением на зажимах источника  , тогда ток в цепи также будет меняться по синусоидальному закону. Ток определяют по формуле
, тогда ток в цепи также будет меняться по синусоидальному закону. Ток определяют по формуле 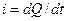 . Количество электричества Q на обкладках конденсатора связано с напряжением на емкости и его емкостью: Q = Cu. Следовательно,
. Количество электричества Q на обкладках конденсатора связано с напряжением на емкости и его емкостью: Q = Cu. Следовательно,
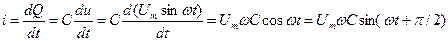 (5.20)
(5.20)
Таким образом, ток в цепи с емкостью опережает по фазе напряжение на угол π/2 (рис. 5.9).
Физически это объясняется тем, что напряжение на емкости возникает за счет разделения зарядов на его обкладках в результате прохождения тока. Следовательно, напряжение появляется только после возникновения тока (сравните процесс появления напряжения на емкости с процессом увеличения уровня жидкости при заполнении бака). Выведем закон Ома для цепи с емкостью. Из выражения (5.20) следует, что 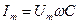 , или
, или
 (5.21)
(5.21)
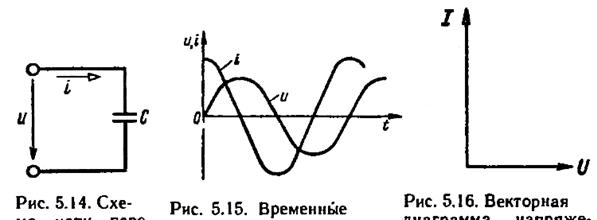 |
Рисунок 5.9 Схема цепи переменного тока с емкостью, временные диаграммы и векторная диаграмма напряжения и тока
Введем обозначение:
 (5.21а)
(5.21а)
где  - емкостное сопротивление цепи.
- емкостное сопротивление цепи.
Тогда выражение закона Ома можно представить в следующем виде:
для амплитудных значений
 (5.22)
(5.22)
для действующих значений
 (5.22а)
(5.22а)
Из формулы (5.21а) и рис. 5.10 следует, что емкостное сопротивление  уменьшается с ростом частоты f. Это объясняется тем, что при большей частоте через поперечное сечение диэлектрика в единицу времени протекает большее количество электричества при том же напряжении, что эквивалентно уменьшению сопротивления цепи.
уменьшается с ростом частоты f. Это объясняется тем, что при большей частоте через поперечное сечение диэлектрика в единицу времени протекает большее количество электричества при том же напряжении, что эквивалентно уменьшению сопротивления цепи.
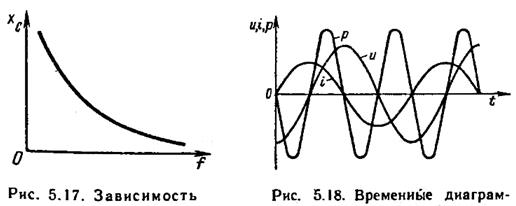 |
Рисунок 5.10 Зависимость емкостного сопротивления XC от частоты f и временные диаграммы напряжения, тока и мгновенной мощности для цепи с емкостью
Рассмотрим энергетические характеристики в цепи с емкостью.
Мгновенная мощность. Пусть начальная фаза тока в цепи равна нулю, тогда  . Так как напряжение на емкости отстает от тока на угол
. Так как напряжение на емкости отстает от тока на угол  , то
, то  или
или 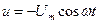 . Выражение для мгновенной мощности примет вид
. Выражение для мгновенной мощности примет вид
 (5.23)
(5.23)
Анализ формулы (5.23) и рис. 5.10 показывает, что в цепи с емкостью, так же как и в цепи с индуктивностью, происходит переход энергии от источника к нагрузке, и наоборот. В данном случае энергия источника преобразуется в энергию электрического поля конденсатора. Из сравнения выражений (5.23) и (5.9) и соответствующих им графиков (рис. 5.10 и 5.9) следует, что если бы индуктивная катушка и конденсатор были включены последовательно, то между ними происходил обмен энергией. Средняя мощность в цепи с емкостью также равна нулю: Р = 0
Реактивная мощность. Для количественной характеристики интенсивности обмена энергией между источником и конденсатором служит реактивная мощность Q=U1