Главная | Обратная связь

Необходимый признак сходимости.

Раздел V. Ряды

При решении ряда математических задач, в том числе и в приложе­ниях математики в экономике, приходится рассматривать суммы, составленные из бесконечного множества слагаемых.

Цель занятия – познакомиться с новым математическим аппаратом – рядами.

Задачазанятия – научиться суммированию бесконечного числа слагаемых

Тема 14. Числовые ряды

14.1. Понятие числового ряда. Сходимость ряда. Необходимый признак сходимости.

14.2. Достаточные признаки сходимости знакоположительных рядов: сравнения, Даламбера, интегральный признак.

14.3. Знакочередующиеся ряды. Признак Лейбница. Условная и абсолют­ная сходимость.

 

Понятие числового ряда. Сходимость ряда.

Необходимый признак сходимости.

Рассмотрим числовую последовательность:

a₁, a₂, a₃,… a_n,…

Определение. Dshf;tybt a₁+a₂+a₃+…+a_n+… (14.1.1)

называется числовым рядом.

Числа a₁, a₂, a₃,… – члены ряда, a_n – общий, или n-ый член ряда.

Ряд (14.1.1) считается заданным, если известен его общий член a_n=f(n), позволяющий найти любой член ряда по его номеру. Для краткости ряд (14.1.1) удобно записывать в виде: (14.1.2)

Например, общий член ряда . Ряд записывается в виде:

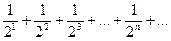
Более трудной является обратная задача: по нескольким членам ряда найти общий член ряда.

Пример 1. Дан ряд Можно убедится, что его общий член .

Сумма nпервых членов ряда S_n называется n-ой частичной суммой ряда.

S₁=a₁

S₂ = a₁ + a₂ = S₁ + a₂

S₃ = a₁ + a₂ + a₃ = S₂ + a₃

_{...........................................................................}

S_n = a₁ + a₂ + … + a_n-1 + a_n = S_n-1 + a_n

Определение. Если существует при конечный предел последовательности частичных сумм, т.е.

, ( 14.1.3)

то ряд называется сходящимся, а число S – суммойряда.

Если конечного предела (14.1.3) не существует, ряд называется расходящимся.

Пример 2. Рассмотрим ряд, составленный из членов бесконечной геометрической прогрессии (14.1.4)

Известно, что сумма n первых членов геометрической прогрессии (а это n-ая частичная сумма ряда)

Найдем предел этой частичной суммы при n

ряд сходится

ряд расходится

 

Если q=1, то ряд (14.4) записывается в виде a + a + a + … + a + … Его частичная сумма S_n=na, , т.е. ряд расходится.

Если q=-1, то ряд (14.1.4) записывается в виде a – a + a – a + …

Его частичная сумма	если n – четное
если n – нечетное

т.е. не существует . Значит, ряд расходится.

Вывод: геометрическая прогрессия сходится только в том случае, если ее знаменатель . Причем сумма ряда (сумма бесконечно убывающей геометрической прогрессии) и расходится, если .

Свойства сходящихся рядов Теорема 14.1.1.Если ряды (А):a1+a2+a3+…+an+… и (B):b1+b2+b3+…+bn+… сходятся и их суммы равны соответственно S(A) и S(B), то ряд (С): (a1+b1)+(a2+b2)+…+(an+bn)+…, полученный почленным сложением (вычитанием) данных рядов также сходится, и его сумма

Доказательство. Обозначим частичные суммы рядов (А) и (В) соответственно S_n(A) = a₁+a₂+a₃+…+a_n; S_n(B) = b₁+b₂+b₃+…+b_n, а частичную сумму ряда (С) s_n = (a₁+b₁)+(a₂+b₂)+…+(a_n+b_n) = =(a₁+a₂+a₃+…+a_n)+ (b₁+b₂+b₃+…+b_n) =

Переходя к пределу при n ® ¥, получаем

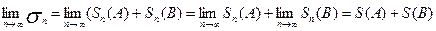
оба предела существуют

Таким образом, существует

Значит, ряд (С) сходится.

Теорема 14.1.2. Если ряд a1+a2+a3+…+an+… (A) сходится к сумме S, то ряд (С): ka1+ka2+ka3+…+kan+…, полученный почленным умножением данного ряда на число k, также сходится, и его сумма s=kS.

Доказательство. Пусть S_n и s_n – частичные суммы рядов (А) и (С).

Найдем: 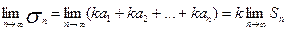, но .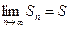

Значит, существует 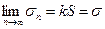. Следовательно, ряд (С) сходится.

Теорема 14.1.3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.

Доказательство. Пусть ряд a₁+a₂+a₃+…+a_n+… (А) сходится к сумме S; S_n – его частичная сумма. Отбросим из частичной суммы ряда (А) k членов, сумма которых равна s_k. Сумму оставшихся членов обозначим s_n-k. Первые n членов всегда можно выбрать таким образом, чтобы отбрасываемые члены находились среди этих n членов. Тогда S_n = s_k+s_n-k. Очевидно,

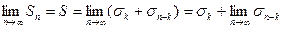
Отсюда ,

т.е. существует предел частичной суммы ряда, полученного из данного путем отбрасывания конечного числа k членов.

Если отбросить в ряде a₁+a₂+a₃+…+a_n+a_n+1+… n первых членов, то получится ряд a_n+1+a_n+2+…, который называется n-ым остатком ряда. Его сумма обозначается через r_n, т.е. r_n = a_n+1+a_n+2+a_n+3+…+a_n+m+…

Из теоремы 14.1.3 следует: если ряд сходится, то и остаток ряда также сходится.

Пусть ряд (А) сходится к сумме S.

Очевидно, S=S_n+r_n. В соответствии со свойствами пределов, если , то |S – S_n| = |r_n| < e при n®¥, а это означает что , т.е. имеет место:

Теорема 14.1.4. Чтобы ряд a1+a2+a3+…+an+… сходился необходимо и достаточно, чтобы остаток ряда rn при n®¥ стремился к нулю.

При решении многих практических, в том числе экономических и финансовых задач, приходится использовать ряды. И одним из важнейших вопросов, является вопрос сходимости ряда. Установить сходимость (расходимость) ряда путем определения S_n и нахождения не всегда просто, а иногда и невозможно. Проще это можно сделать на основании признаков сходимости рядов.