Главная | Обратная связь

Интегральный признак

Теорема 14.1.11. Пусть дан ряд с положительными членами a1+a2+…+an+…, которые не возрастают, т.е. a1³a2³a3³…³an (возможно с некоторого номера N) и пусть при x³1 существует непрерывная, положительная невозрастающая функция f(x), такая, что f(n)=an, т.е. f(1)=a1, f(2)=a2,…, f(k)=ak,… Тогда ряд сходится (или расходится) одновременнос несобственным интегралом .

Доказательство. Пусть выполняется условие f(n)=a_n для функции f(x). Построим график этой функции для x³1 и рассмотрим площадь вписанной ступенчатой фигуры для 1£x£n.

S_{впис.ступ.фиг.} = a₁+a₂+…+a_n

Если частичная сумма ряда равна S_n, то S_{впис.ступ.фиг.} = S_n – a₁. Площадь криволинейной трапеции под кривой f(x) для 1£x£n . Очевидно, 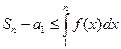. Тогда .

Пусть несобственный интеграл сходится к числу А. Тогда S_n<A+a₁, т.е. последовательность частичных сумм ограничена. С другой стороны эта последовательность монотонно возрастает, т.к. в силу положительности членов ряда (а_n>0) S_n < S_n+1 = S_n + a_n+1. Из ограниченности и монотонности частичных сумм S_n следует, что существует (см. признаки существования пределов). Ряд сходится.

Пусть несобственный интеграл , т.е. интеграл расходится. Сравним площади описанной ступенчатой фигуры для 1£x£n и рассмотренной выше криволинейной трапеции

S_{оп.ст.фиг.}=a₁+a₂+…+ a_n-1=S_n-a_n.

Очевидно, S_n-a_n³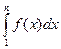 ,или S_n≥ 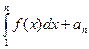.Перейдем к пределу при n→¥:

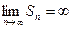,, следовательно (по определению), ряд расходится.

В качестве примера рассмотрим обобщенный гармонический ряд , где α – любое действительное число.

Решение. Как известно, функция при x ≥ 1 положительная и невозрастающая. Как было показано выше ( ) несобственный интеграл сходится при α > 1 и расходится при α ≤ 1. Следовательно, и обобщенный гармонический ряд сходится, если α > 1 и расходится, если α≤1. В связи с достаточной простотой ответа о сходимости обобщенного гармонического ряда, его удобно использовать, как было сказано выше (п. 14.2), в качестве эталонного ряда.

Следует отметить, что трудности использования интегрального признака могут возникнуть при вычислении несобственных интегралов .

Замечание. В соответствии со свойствами интегралов , но . Следовательно, при использовании интегрального признака можно вычислять несобственный интеграл .

Примеры. Исследовать сходимость рядов.

1. 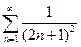. Рассмотрим . Введем новую переменную t=2n+1. Если n=1, t=3; если n=¥, t=¥. После замены получаем , который сходится при t ≥ 1, а значит, и при t ≤ 3, т.к. p = 2 > 1. Ряд сходится.

2. . Сравним этот ряд с рядом .

для n ≥ 3.

Эталонный обобщенный гармонический ряд расходится, т.к. . В таком случае и ряд расходится, т.к. получен путем отбрасывания первых двух членов из эталонного ряда. В таком случае на основании признака сравнения расходится ряд , а значит, и данный ряд расходится (теорема 14.1.3).