 |
|
Понятие числового положительного ряда
Ряды для чайников. Примеры решений
Всех выживших приветствую на втором курсе! На этом уроке, а точнее, на серии уроков, мы научимся управляться с рядами. Тема не очень сложная, но для ее освоения потребуются знания с первого курса, в частности, необходимо понимать, что такое предел, и уметь находить простейшие пределы. Впрочем, ничего страшного, по ходу объяснений я буду давать соответствующие ссылки на нужные уроки. Некоторым читателям тема математических рядов, приемы решения, признаки, теоремы могут показаться своеобразными, и даже вычурными, нелепыми. В этом случае не нужно сильно «загружаться», принимаем факты такими, какими они есть, и просто учимся решать типовые, распространенные задания.
Рекомендую следующий порядок изучения темы:
1) Ряды для чайников (эта статья) + нахождение суммы ряда.
2) Признак Даламбера. Признаки Коши.
3) Знакочередующиеся ряды. Признак Лейбница.
4) Ряды повышенной сложности – для тех, кому не хватило обычных =)
Понятие числового положительного ряда
В общем виде положительный числовой ряд можно записать так: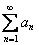 
.
Здесь:
– математический значок суммы;
– общий член ряда (запомните этот простой термин);
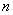– переменная-«счётчик». Запись 
обозначает, что проводится суммирование от 1 до «плюс бесконечности», то есть, сначала у нас 
, затем 
, потом 
, и так далее – до бесконечности. Вместо переменной 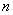иногда используется переменная 
или 
. Суммирование не обязательно начинается с единицы, в ряде случаев оно может начинаться с нуля 
, с двойки 
либо с любого натурального числа.
В соответствии с переменной-«счётчиком» любой ряд можно расписать развёрнуто:
– и так далее, до бесконечности.
Будем считать, что ВСЕ слагаемые 
– это неотрицательные ЧИСЛА. То есть, на данном уроке речь пойдет о положительных числовых рядах.
Пример 1
Записать первые три члена ряда
Это уже, кстати, «боевое» задание – на практике довольно часто требуется записать несколько членов ряда.
Сначала , тогда: 
Затем , тогда: 
Потом , тогда: 
Процесс можно продолжить до бесконечности, но по условию требовалось написать первые три члена ряда, поэтому записываем ответ: 
Обратите внимание на принципиальное отличие от числовой последовательности,
в которой члены не суммируются, а рассматриваются как таковые.
Пример 2
Записать первые три члена ряда
Это пример для самостоятельного решения, ответ в конце урока
Даже для сложного на первый взгляд ряда не составляет трудности расписать его в развернутом виде:
Пример 3
Записать первые три члена ряда
На самом деле задание выполняется устно: мысленно подставляем в общий член ряда сначала , потом и . В итоге:
Ответ оставляем в таком виде, полученные члены ряда лучше не упрощать, то есть не выполнять действия: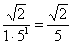 
, 
, 
. Почему? Ответ в виде 
гораздо проще и удобнее проверять преподавателю.
Иногда встречается обратное задание
Пример 4
Записать сумму в свёрнутом виде с общим членом ряда
Здесь нет какого-то четкого алгоритма решения, закономерность нужно просто увидеть.
В данном случае:
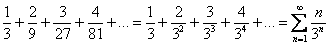
Для проверки полученный ряд 
можно «расписать обратно» в развернутом виде.
А вот пример чуть сложнее для самостоятельного решения:
Пример 5
Записать сумму в свёрнутом виде с общим членом ряда
Выполнить проверку, снова записав ряд в развернутом виде
Сходимость числовых положительных рядов
Необходимый признак сходимости ряда
Одной из ключевых задач теории числовых рядов является исследование ряда на сходимость. При этом возможны два случая:
1) Ряд 
расходится. Это значит, что бесконечная сумма равна бесконечности: 
. Хороший пример расходящегося числового ряда встретился в начале урока: 
. Здесь совершенно очевидно, что каждый следующий член ряда – больше, чем предыдущий, поэтому 
и, значит, ряд расходится. Чуть ниже мы рассмотрим более строгий математический критерий для данного примера.
2) Ряд сходится. Это значит, что бесконечная сумма равна некоторому конечному числу 
: 
. В качестве примера сходящегося числового ряда можно привести бесконечно убывающую геометрическую прогрессию, известную нам со школы: 
. Сумму членов бесконечно убывающей геометрической прогрессии можно найти по формуле: 
, где 
– первый член прогрессии, 
– основание прогрессии. В данном случае: 
, 
. Таким образом: 
Получено конечное число, значит, ряд 
сходится, что и требовалось доказать.
В подавляющем большинстве случаев найти сумму ряда затруднительно, и поэтому на практике для исследования сходимости ряда используют специальные признаки, которые доказаны теоретически.
Существует несколько признаков сходимости ряда: необходимый признак сходимости ряда, признаки сравнения, признак Даламбера, признаки Коши, некоторые другие признаки. Когда какой признак применять? Это зависит от общего члена ряда , образно говоря – от «начинки» ряда. На этом уроке мы рассмотрим необходимый признак сходимости ряда и признаки сравнения.
!Для дальнейшего усвоения урока необходимо хорошо понимать, что такое предел и хорошо уметь раскрывать неопределенность вида 
. Для повторения материала обратитесь к статье Пределы. Примеры решений.