 |
|
Предельный признак сравнения числовых положительных рядов
Рассмотрим два положительных числовых ряда 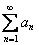 и
и 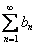 . Если предел отношения общих членов этих рядов равен конечному, отличному от нуля числу
. Если предел отношения общих членов этих рядов равен конечному, отличному от нуля числу  :
:  , то оба ряда сходятся или расходятся одновременно.
, то оба ряда сходятся или расходятся одновременно.
Когда применяется предельный признак сравнения?Предельный признак сравнения применяется тогда, когда «начинкой» ряда у нас являются многочлены. Либо один многочлен в знаменателе, либо многочлены и в числителе и в знаменателе. Один или оба многочлена также могут находиться под корнем.
Разделаемся с рядом, для которого забуксовал предыдущий признак сравнения.
Пример 10
Исследовать ряд на сходимость 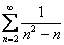
Сравним данный ряд со сходящимся рядом  . Используем предельный признак сравнения. Известно, что ряд
. Используем предельный признак сравнения. Известно, что ряд  – сходится. Если нам удастся показать, что
– сходится. Если нам удастся показать, что  равен конечному, отличному от нуля числу, то будет доказано, что ряд
равен конечному, отличному от нуля числу, то будет доказано, что ряд  – тоже сходится.
– тоже сходится.

Получено конечное, отличное от нуля число, значит, исследуемый ряд сходится вместе с рядом  .
.
Почему для сравнения был выбран именно ряд  ? Если бы мы выбрали любой другой ряд из «обоймы» обобщенного гармонического ряда, то у нас не получилось бы в пределе конечного, отличного от нуля числа (можете поэкспериментировать).
? Если бы мы выбрали любой другой ряд из «обоймы» обобщенного гармонического ряда, то у нас не получилось бы в пределе конечного, отличного от нуля числа (можете поэкспериментировать).
Примечание: когда мы используем предельный признак сравнения, не имеет значения, в каком порядке составлять отношение общих членов, в рассмотренном примере отношение можно было составить наоборот: 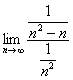 – это не изменило бы сути дела.
– это не изменило бы сути дела.
Предельный признак сравнения применим почти для всех рядов, которые мы рассмотрели в предыдущем пункте:
 ,
,  ,
,  ,
,  .
.
Данные ряды по только что рассмотренной трафаретной схеме нужно предельно сравнить соответственно со сходящимися рядами:
 ,
,  ,
,  ,
, 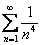 .
.
Пример 11
Исследовать ряд на сходимость 
Это пример для самостоятельного решения.
Что делать, если многочлены находятся и в знаменателе, и в числителе? Алгоритм решения почти такой же – нам нужно подобрать для сравнения подходящий ряд из «обоймы» обобщенного гармонического ряда.
Пример 12
Исследовать ряд на сходимость 
Мы видим, что и в числителе и в знаменателе у нас многочлены, причем, в знаменателе многочлен находится под корнем. Подбираем ряд для сравнения  .
.
1) Сначала нужно найти старшую степень знаменателя. Если бы не было корня, то, понятно, что старшая степень знаменателя равнялась бы четырем. Что делать, когда есть корень? Об этом я уже рассказывал на уроке Методы решения пределов. Повторение – мать учения: мысленно или на черновике отбрасываем все члены, кроме старшего:  . Если есть константа, её тоже отбрасываем:
. Если есть константа, её тоже отбрасываем:  . Теперь извлекаем корень:
. Теперь извлекаем корень:  . Таким образом, старшая степень знаменателя равна двум.
. Таким образом, старшая степень знаменателя равна двум.
2) Выясняем старшую степень числителя. Очевидно, что она равна единице.
3) Из старшей степени знаменателя вычитаем старшую степень числителя: 2 – 1 = 1
Таким образом, наш ряд нужно сравнить с рядом  , то есть, с расходящимся гармоническим рядом.
, то есть, с расходящимся гармоническим рядом.
По мере накопления опыта решения эти три пункта можно и нужно проводить мысленно.
Само оформление решения должно выглядеть примерно так:
”
Сравним данный ряд с расходящимся гармоническим рядом  . Используем предельный признак сравнения:
. Используем предельный признак сравнения:
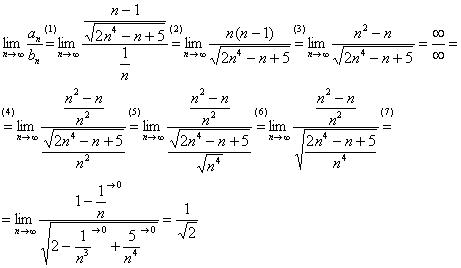
Получено конечное, отличное от нуля число, значит, исследуемый ряд расходится вместе с гармоническим рядом  .
.
”
(1) Составляем отношение общих членов.
(2) Избавляемся от четырехэтажности дроби.
(3) Раскрываем в числителе скобки.
(4) Неопределенность  устраняем стандартным способом деления числителя и знаменателя на «эн» в старшей степени.
устраняем стандартным способом деления числителя и знаменателя на «эн» в старшей степени.
(5) В самой нижней строке подготавливаем  для внесения под корень:
для внесения под корень: 
(6) В знаменателе организуем общий корень.
Примечание: на практике пункты 5,6 можно пропустить, я их очень подробно разжевал для тех, кто не очень понимает, как обращаться с корнями.
(7) Почленно делим числители на знаменатели. Помечаем члены, которые стремятся к нулю.
Пример 13
Исследовать ряд на сходимость 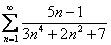
Это пример для самостоятельного решения.
В недалёком будущем вы будете сразу видеть, сходится такой ряд или расходится. Например, рассмотрим ряд 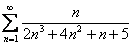 . Ага, 3 – 1 = 2, значит, ряд нужно сравнить со сходящимся рядом
. Ага, 3 – 1 = 2, значит, ряд нужно сравнить со сходящимся рядом  , и сразу можно сказать, что наш исследуемый ряд тоже сходится. Дело за малым – осталось аккуратно оформить стандартное рутинное решение.
, и сразу можно сказать, что наш исследуемый ряд тоже сходится. Дело за малым – осталось аккуратно оформить стандартное рутинное решение.
Вот, пожалуй, и все начальные сведения о положительных числовых рядах, которые потребуются вам при решении практических примеров. Следующий урок по теме числовых рядов – Признаки сходимости рядов. Признак Даламбера. Признаки Коши
Желаю успехов!
Решения и ответы:
Пример 2: 
Примечание: обратите внимание, что переменная-«счётчик» в данном примере «заряжается» со значения 
Пример 5: 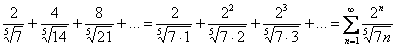
Пример 7:

Делим числитель и знаменатель на 

Исследуемый ряд расходится, так как не выполнен необходимый признак сходимости ряда.
Пример 9:
Сравним данный ряд с расходящимся гармоническим рядом  .
.
Используем признак сравнения:
Если  , то
, то 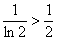
Если  , то
, то 
Если  , то
, то 
Таким образом, для всех членов ряда выполнено неравенство  , значит, по признаку сравнения исследуемый ряд расходитсявместе с гармоническим рядом
, значит, по признаку сравнения исследуемый ряд расходитсявместе с гармоническим рядом  .
.
Примечание: И здесь есть неформальный смысл. Доказано, что гармонический ряд расходится, следовательно, сумма его членов:  . Мы показали, что члены ряда
. Мы показали, что члены ряда 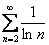 ещё больше членов ряда
ещё больше членов ряда  , и совершенно понятно, что сумма ряда
, и совершенно понятно, что сумма ряда 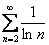 не может быть меньше бесконечности.
не может быть меньше бесконечности.
Пример 11:
Сравним данный ряд с расходящимся рядом  . Используем предельный признак сравнения:
. Используем предельный признак сравнения:

Получено конечное, отличное от нуля число, значит, исследуемый ряд расходится вместе с рядом  .
.
Пример 13:
Эти 3 пункта выполняем мысленно или на черновике:
1) Старшая степень знаменателя:4
2) Старшая степень числителя: 1
3) 4 – 1 = 3
Сравним данный ряд со сходящимся рядом 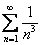 . Используем предельный признак сравнения:
. Используем предельный признак сравнения:

Получено конечное число, отличное от нуля, значит, исследуемый ряд сходится вместе с рядом 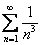 .
.