 |
|
Что такое сумма ряда?
Строгое определение сходимости/расходимости и суммы ряда в теории даётся через так называемые частичные суммы ряда. Частичные – значит неполные. Распишем частичные суммы числового ряда 
:
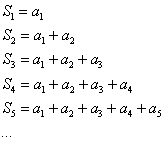
И особую роль играет частичная сумма «эн» членов ряда:
Если предел частичных сумм числового ряда 
равен конечному числу: 
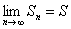, то такой ряд называют сходящимся, а само число 
– суммой ряда. Если же предел 
бесконечен либо его не существует, то ряд называют расходящимся.
Вернёмся к демонстрационному ряду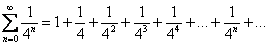 
и распишем его частичные суммы:
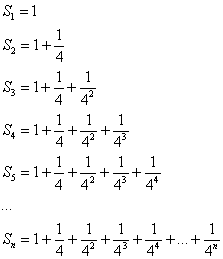
Предел частичных сумм 
– есть в точности бесконечно убывающая геометрическая прогрессия, сумма которой равна: 
. Похожий предел мы рассматривали на уроке о числовых последовательностях. Собственно, и сама формула 
– это прямое следствие вышеизложенных теоретических выкладок (см. 2-ой том матана).
Таким образом, прорисовывается общий алгоритм решения нашей задачи: необходимо составить энную частичную сумму ряда 
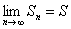и найти предел . Посмотрим, как это осуществляется на практике:
Пример 3
Вычислить сумму ряда
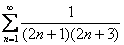
Решение: на первом шаге нужно разложить общий член ряда в сумму дробей. Используем метод неопределённых коэффициентов:
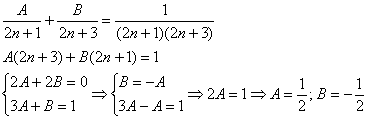
В результате:
Сразу же полезно провести обратное действие, выполнив тем самым проверку:
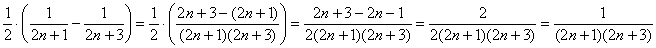
Получен общий член ряда в исходном виде, следовательно, разложение в сумму дробей проведено успешно.
Теперь составим частичную сумму ряда 
. Вообще это делается устно, но один раз я максимально подробно распишу, что откуда взялось:
Как записать 
совершенно понятно, но чему равен предыдущий член 
? В общий член ряда 
ВМЕСТО «эн» подставляем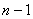 
:
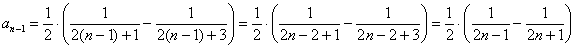
Почти все слагаемые частичной суммы благополучно сокращаются:
Прямо такие пометки и делаем карандашом в тетради. Чертовски удобно.
Осталось вычислить элементарный предел и узнать сумму ряда:
Ответ: 
Аналогичный ряд для самостоятельного решения:
Пример 4
Вычислить сумму ряда
Примерный образец чистового оформления решения в конце урока.
Очевидно, что нахождение суммы ряда – это само по себе доказательство его сходимости (помимо признаков сравнения, Даламбера, Коши и др.), о чём, в частности, намекает формулировка следующего задания:
Пример 5
Найти сумму ряда или установить его расходимость
По внешнему виду общего члена можно сразу сказать, как ведёт себя этот товарищ. Без комплексов. С помощью предельного признака сравнения легко выяснить (причём даже устно), что данный ряд будет сходиться вместе с рядом 
. Но перед нами редкий случай, когда без особых хлопот рассчитывается ещё и сумма.
Решение: разложим знаменатель дроби в произведение. Для этого нужно решить квадратное уравнение:
Таким образом:
Множители лучше расположить в порядке возрастания: 
.
Выполним промежуточную проверку:
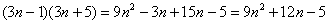
ОК
Таким образом, общий член ряда:
Методом неопределённых коэффициентов разложим его в сумму дробей:
Коэффициенты получились целые и это радует:
На всякий случай выполним ещё одну промежуточную проверку:
ОК
Поэтапные проверки – королевы зачётов ;-)
Составим энную частичную сумму и сократим всё, что можно сократить:
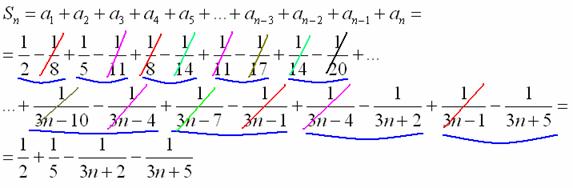
Как видите, в этот раз противоположные числа не расположены рядышком. Поэтому на практике всегда лучше перестраховаться и записать побольше членов ряда – чтобы наверняка понять, какие слагаемые сократятся, а какие – нет. По той же причине крайне желательно выполнять пометки карандашом.
Опыт показывает, что чаще всего студенты испытывают затруднения с хвостом суммы. В этой связи ещё раз повторим принцип, по которому записаны члены 
. Отчего ж не повторить?
В общий член ряда 
:
– ВМЕСТО «эн» подставляем 
: 
;
– ВМЕСТО «эн» подставляем 
: 
;
– ВМЕСТО «эн» подставляем :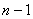 
.
На завершающем этапе находим сумму ряда:
Ответ: 
Изящный ряд для самостоятельного решения:
Пример 6
Найти сумму ряда или установить его расходимость
Решение и ответ в конце урока.
Вероятно, на этом рубеже у многих посетителей возникла уверенность в своих навыках и желание раствориться на просторах Интернета. Рекомендую немного задержаться, поскольку ниже по течению среди, казалось бы, такого однообразия приветливо моргают глазами большие крокодилы.
Усложняем задание и набиваем руку:
Пример 7
Вычислить сумму ряда
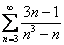
Решение: со знаменателем тут никаких проблем:
Множители, как я уже отмечал, целесообразно расположить в порядке возрастания.
Используем метод неопределённых коэффициентов:
Здесь на последних шагах проведено почленное сложение двух уравнений системы.
Таким образом: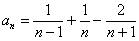 
Не ленимся:
Что и требовалось проверить.
Запишем частичную сумму «эн» членов ряда, при этом обращаем внимание на тот факт, что «счётчик» ряда «начинает работать» с номера 
. Как и в предыдущих примерах, надёжнее растянуть кобру на приличную длину:
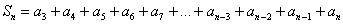
Однако если мы запишем в одну-две строчки, то всё равно будет довольно трудно сориентироваться в сокращениях слагаемых (их таки 3 в каждом члене). И здесь нам на помощь придёт… геометрия. Заставим плясать змею под свою дудочку:
Да, прямо так и пишем в тетради один член под другим и прямо так их вычёркиваем. Кстати, собственное изобретение. Как понимаете, не от самого лёгкого задания в этой жизни =)
В результате всех сокращений получаем:
И, наконец, сумма ряда:
Ответ: 
Готово.
Пример 8
Вычислить сумму ряда
Это пример для самостоятельного решения.
Рассматриваемая задача, конечно, не радует нас разнообразием – на практике встречается либо бесконечно убывающая геометрическая прогрессия, либо ряд с дробно-рациональным общим членом и разложимым многочленом в знаменателе (к слову, далеко не каждый такой многочлен даёт возможность найти сумму ряда). Но, тем не менее, иногда попадаются необычные экземпляры, и по сложившейся доброй традиции я завершаю урок какой-нибудь любопытной задачей:
Пример 9
Вычислить сумму ряда, если она существует
Решение: формулировка уже интригует. Интересен тот факт, что все члены данного ряда отрицательны. Почему? На интервале 
логарифм меньше нуля, а за счёт аргумента 
при любом натуральном «эн» (начиная с 
) мы каждый раз и попадаем в этот интервал.
Таким образом, если ряд сходится, то будет отрицательна и его сумма. Только вот есть мааааленькая проблемка – найти это значение, если оно существует =)
Алгоритм такой же, главное, догадаться, с какой стороны подступиться к решению. Предыдущий опыт подсказывает, что нужно попытаться представить общий член ряда в виде суммы двух или бОльшего количества слагаемых. Из этих соображений преобразуем выражение в скобках и используем свойства логарифма:
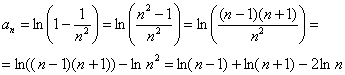
Ну что же, выглядит вполне перспективно, давайте разберёмся с частичной суммой ряда:
В целях устранения неопределённости вновь используем свойство логарифма:
Получено конечное число, а значит, ряд сходится. Как и ожидалось, сумма получилась отрицательной.
Ответ: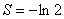 
Поздравляю со знаменательным событием! Коль скоро вы читаете эти строки, то сегодня на вашу долю выпал редкий и счастливый случай – когда в частичной сумме ряда удалось массово сократить слагаемые. Удалось же? =)
Не каждый день бывает!
Решения и ответы:
Пример 2: Решение:
Дважды используем формулу для нахождения суммы бесконечно убывающей геометрической прогрессии: .
Для первого ряда: 
, для второго ряда: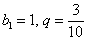 
.
Ответ: сумма ряда 
Пример 4: Решение:Методом неопределенных коэффициентов разложим общий член ряда в сумму дробей:
Таким образом:
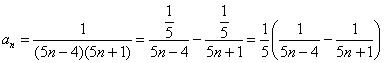
Найдём частичную сумму ряда:
Вычислим сумму ряда:
Ответ: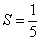 
Пример 6: Решение: разложим знаменатель общего члена в произведение и методом неопределённых коэффициентов получим сумму дробей:
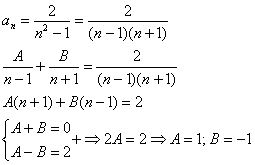
Таким образом: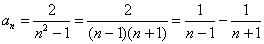 
Составим частичную сумму и проведём сокращения:
Вычислим сумму ряда:
Ответ: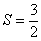 
Пример 8: Решение: представим общий член ряда в виде:
Методом неопределённых коэффициентов разложим его в сумму дробей:
Таким образом: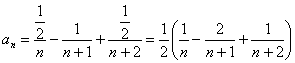 
Запишем частичную сумму:
Вычислим сумму ряда:
Ответ: 
Признаки сходимости рядов.
Признак Даламбера. Признаки Коши
Работайте, работайте – а понимание придёт потом
Ж.Л. Даламбер
Всех поздравляю с началом учебного года! Сегодня 1-ое сентября, и я решил в честь праздника познакомить читателей с тем, что вы давно с нетерпением ждали и жаждали узнать – признаками сходимости числовых положительных рядов. Праздник Первое сентября и мои поздравления всегда актуальны, ничего страшного, если на самом деле за окном лето, вы же сейчас в третий раз пересдаете экзамен учитесь, если зашли на эту страничку!
Для тех, кто только начинает изучать ряды, рекомендую для начала ознакомиться со статьей Числовые ряды для чайников. Собственно, данная телега является продолжением банкета. Итак, сегодня на уроке мы рассмотрим примеры и решения по темам:
Признак сходимости Даламбера
Радикальный признак сходимости Коши
Интегральный признак сходимости Коши
Одним из распространенных признаков сравнения, который встречается в практических примерах, является признак Даламбера. Признаки Коши встречаются реже, но тоже весьма популярны. Как всегда, постараюсь изложить материал просто, доступно и понятно. Тема не самая сложная, и все задания в известной степени трафаретны.