 |
|
Признаки сравнения для положительных числовых рядов
Существуют два признака сравнения, один из них я буду называть просто признаком сравнения, другой – предельным признаком сравнения.
Сначала рассмотрим признак сравнения. На практике он встречается довольно редко, но эта статья была бы неполной без данной информации.
Признак сравнения:Рассмотрим два положительных числовых ряда 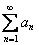 и
и 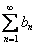 . Если известно, что ряд
. Если известно, что ряд 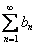 – сходится, и выполнено неравенство
– сходится, и выполнено неравенство  (для
(для  ), то ряд
), то ряд 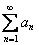 тоже сходится.
тоже сходится.
Иными словами: Из сходимости ряда с бОльшими членами следует сходимость ряда с меньшими членами.
Пример 8
Исследовать ряд на сходимость 
Заглядываем в «пачку» обобщенного гармонического ряда и находим похожий ряд:  Из теории известно, что он сходится. Теперь нам нужно показать, что для всех значений
Из теории известно, что он сходится. Теперь нам нужно показать, что для всех значений  справедливо неравенство
справедливо неравенство 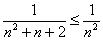 .
.
Если  , то
, то 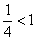
Если  , то
, то 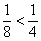
Если  , то
, то 
Если  , то
, то 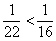
….
И так далее.
Оформить решение можно так:
“
Сравним исследуемый ряд со сходящимся рядом  . Используем признак сравнения. Для рассматриваемых рядов выполнено неравенство
. Используем признак сравнения. Для рассматриваемых рядов выполнено неравенство 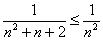 , значит, по признаку сравнения исследуемый ряд сходится вместе с рядом
, значит, по признаку сравнения исследуемый ряд сходится вместе с рядом  .
.
”
В принципе, можно расписать и подробнее, указав, что неравенство выполняется для нескольких первых членов.
Проанализируем признак сравнения и решенный пример с неформальной точки зрения. Все-таки, почему ряд  сходится? А вот почему. Если ряд
сходится? А вот почему. Если ряд  сходится, то он имеет некоторую конечную сумму
сходится, то он имеет некоторую конечную сумму  :
: 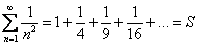 . И поскольку все члены ряда
. И поскольку все члены ряда  меньше соответствующих членов ряда
меньше соответствующих членов ряда  , то ясен пень, что сумма ряда
, то ясен пень, что сумма ряда  не может быть больше числа
не может быть больше числа  , и тем более, не может равняться бесконечности!
, и тем более, не может равняться бесконечности!
Аналогично можно доказать сходимость «похожих» рядов:  ,
,  ,
,  и т.д.
и т.д.
! Обратите внимание, что во всех случаях в знаменателях у нас находятся «плюсы». Наличие хотя бы одного минуса может серьёзно осложнить использование рассматриваемого признака сравнения. Например, если ряд  таким же образом сравнить со сходящимся рядом
таким же образом сравнить со сходящимся рядом 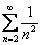 ( выпишите несколько неравенств для первых членов), то условие
( выпишите несколько неравенств для первых членов), то условие  не будет выполняться вообще! Здесь можно извернуться и подобрать для сравнения другой сходящийся ряд, например,
не будет выполняться вообще! Здесь можно извернуться и подобрать для сравнения другой сходящийся ряд, например,  , но это повлечёт за собой лишние оговорки и другие ненужные трудности. Поэтому для доказательства сходимости ряда
, но это повлечёт за собой лишние оговорки и другие ненужные трудности. Поэтому для доказательства сходимости ряда  гораздо проще использовать предельный признак сравнения (см. следующий параграф).
гораздо проще использовать предельный признак сравнения (см. следующий параграф).
Пример 9
Исследовать ряд на сходимость 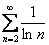
В примере я предлагаю самостоятельно рассмотреть вторую «зеркальную» часть теоремы: Если известно, что ряд 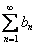 – расходится, и выполнено неравенство
– расходится, и выполнено неравенство 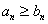 (для
(для  ), то ряд
), то ряд 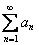 тоже расходится.
тоже расходится.
Иными словами: Из расходимости ряда с меньшими членами следует расходимость ряда с бОльшими членами.
Что нужно сделать?
Нужно сравнить исследуемый ряд с расходящимся гармоническим рядом  : построить несколько неравенств и сделать вывод о справедливости неравенства
: построить несколько неравенств и сделать вывод о справедливости неравенства 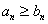 .
.
Решение и образец оформления в конце урока.
Как уже отмечалось, на практике только что рассмотренный признак сравнения применяют редко. Настоящей «рабочей лошадкой» числовых рядов является предельный признак сравнения, и по частоте использования с ним может конкурировать разве что признак Даламбера.