 |
|
Основные определения.
Числовые ряды.
Пусть дана бесконечная числовая последовательность 
.
Числовым рядом называется составленная из членов этой последовательности запись
. (18.1.1)
Эквивалентная (18.1.1) форма записи ряда - с применением символа суммы: 
.
Числа называют членами ряда;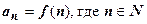 
, называется общим членом ряда. В результате вычисления значений этой функции при n=1, n=2, n=3, … должны получаться члены ряда 
.
Примеры. 1. Пусть 
. Записать ряд.
При n=1 получаем 
, при n=2 
, при n=3 
и т.д., ряд имеет вид 
.
2. Пусть ряд имеет вид 
. Придумать формулу общего члена.
Эта задача имеет много решений, мы придумаем одно из них. Числители растут линейно с n с шагом 2, поэтому в формуле для числителя должно содержаться 2n. Подбором убеждаемся, что для числителей верна формула 2n-1 (=1 при n =1, 3 при n =2 и т.д.). Также подбором убеждаемся, что для знаменателей можно взять формулу 
, поэтому 
. Если нумерацию членов ряда начать с n = 0, то 
.
Основным понятием теории рядов является понятие сходимости числового ряда. Пусть дан ряд (18.1.1). Составим из его членов конечные суммы, называемые частичными суммами ряда: 
Определение. Если существует конечный предел S последовательности частичных сумм ряда (18.1.1) при 
, то говорят, что ряд сходится; число S называют суммой ряда и пишут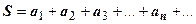 
или 
.
Если 
не существует (в том числе бесконечен), ряд называется расходящимся.
Примеры. 1. Ряд 1+1+1+…+1+…, очевидно, расходится, так как 
.
2. Ряд 1-1+1-…+(-1)n-1+… тоже расходится, так как 
и вообще 
а такая последовательность предела не имеет.
Дальше мы рассмотрим два ряда, к которым в той или иной мере будет сводиться большинство рядов: геометрическую прогрессию и гармонический ряд.
3. Геометрической прогрессией называется ряд 
. (18.1.2)
Число q называют знаменателем прогрессии. Сразу отметим, что при 
ряд расходится. При 
получаем ряд 
структуры, рассмотренной в примере 1, при 
- ряд 
структуры, рассмотренной в примере 2. Пусть теперь 
. Выведем формулу для частичных сумм. Пусть 
, тогда 
. Легко убедиться, что 
. Решая это уравнение относительно 
, получим 
. В этом выражении от n зависит только 
, при этом 
Следовательно, конечный существует при 
, и 
. Итак, геометрическая прогрессия сходится, если её знаменатель удовлетворяет условию , и её сумма равна 
.
4. Гармоническим рядом называется ряд
. (18.1.3)
Докажем, что этот ряд расходится. Рассмотрим частичные суммы с числом слагаемых, равных степеням числа 2: 
.
Сумма членов в каждой скобке больше 1/2: 
, 
, 
и т.д. Таким образом, 
. Последовательность, у которой есть стремящаяся к бесконечности подпоследовательность, не может иметь конечного предела, поэтому гармонический ряд расходится.
В дальнейшем мы редко будем находить сумму ряда; в основном, будет ставиться вопрос о сходимости или расходимости ряда. Для вычисления суммы обычно применяются разложения в ряд элементарных функций, которые мы будем изучать дальше, или искусственные приёмы, например, разложения функции 
на простые слагаемые:
5. 
. Если общий член ряда представить в виде суммы простых слагаемых 
, то 
. Итак, этот ряд сходится, и его сумма равна 1.