Главная | Обратная связь

Равномерная сходимость функционального ряда.

Факт сходимости ряда к своей сумме в точке сходимости х означает, в соответствии с определением предела, то, что для любого числа существует такое натуральное N, что при n>N верно . Здесь - частичная сумма ряда в точке х. Число N зависит, естественно, от 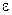, но оно зависит и от х, т.е. . В некоторых точках области сходимости ряд может сходиться к своей сумме быстро, т.е. неравенство будет выполняться при не очень больших значениях N, в других точках эта сходимость может быть медленной. Если ряд сходится к своей сумме примерно с одинаковой скоростью во всех точках х, то сходимость называется равномерной. Более точно, говорят, что ряд сходится равномерно на области G, если для любого числа существует такое натуральное число , одно и то же для всех точек 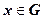,что при n>N выполняется неравенство (или, что тоже самое, , где - остаток ряда после n-го члена).

Понятие равномерной сходимости - одно из фундаментальных понятий функционального анализа. Именно равномерная сходимость обеспечивает сохранение суммой ряда хороших свойств своих членов. Чтобы осознать смысл и значение этого понятия, требуется время, которого у нас, к сожалению, нет. К счастью, имеется простой и понятный достаточный признак равномерной сходимости - признак Вейерштрасса.

Признак Вейерштрасса. Если существует такой положительный сходящийся числовой ряд , что члены функционального ряда в любой точке 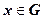удовлетворяют неравенству , то функциональный ряд сходится равномерно в области G.

х

Числовой ряд, удовлетворяющий неравенству , называется мажорирующим рядом, или мажорантой функционального ряда; про функциональный ряд говорят, что он мажорируется числовым рядом.

Рассмотрим примеры, приведённые в начале раздела. Геометрическая прогрессия равномерно сходится на любом отрезке , целиком лежащем в области сходимости (-1,1). Действительно, построим мажоранту для геометрической прогрессии на . Из чисел а, b выберем большее по модулю. Пусть, например, . Тогда для любого выполняется . Таким образом, сходящийся (так как ) числовой ряд мажорирует на функциональный ряд , откуда, по признаку Вейерштрасса, следует равномерная сходимость этого функционального ряда.

Ряд равномерно сходится на любой полуоси , так как на этом множестве он мажорируется рядом .

Ряд равномерно сходится на всей числовой оси (мажоранта для этого ряда уже получена - это ряд ).