Главная | Обратная связь

Свойства сходящихся рядов и их сумм.

В разделе 1.2. Свойства сходящихся рядов мы сформулировали и доказали некоторые из этих свойств. Напомним:

1.5.1. Необходимый признак сходимости ряда. Общий член сходящегося ряда стремится к нулю: .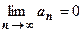

1.5.2. Если сходится ряд, то сходится любой его остаток, Обратно, если сходится какой-нибудь остаток ряда, то сходится и сам ряд.

1.5.3. Если ряд сходится, то сумма его остатка после n-го члена стремится к нулю при .

1.5.4. Если все члены сходящегося ряда умножить на одно и то же число с, то сходимость ряда сохранится, а сумма умножится на с.

1.5.5.Два сходящихся ряда можно почленно складывать и вычитать, полученный ряд также сходится, и его сумма равна, соответственно, сумме или разности исходных рядов.

Сформулируем ещё несколько свойств сходящихся рядов.

1.5.6. Сочетательное свойство сходящегося ряда.Если члены сходящегося ряда сгруппировать произвольным образом: (здесь - строго возрастающая последовательность натуральных чисел), и составить новый ряд из сумм членов в каждой паре круглых скобок, то этот новый ряд тоже будет сходиться, и его сумма будет равна сумме исходного ряда.

Доказательство.Последовательность частичных сумм нового ряда является подпоследовательностью последовательности частичных сумм исходного ряда и сходится к той же сумме.

Все сформулированные свойства полностью аналогичны свойствам конечных сумм, хотя и здесь есть свои тонкости. Так, для конечных сумм можно не только расставлять, но и раскрывать скобки; при этом сумма не меняется. Для рядов это неверно. Пример: если в сходящемся ряде 0+0+0+…+0+… = (1-1) + (1-1)+(1-1)+….+(1-1)+… раскрыть скобки, то получится расходящийся ряд 1-1+1-1+1-1+… . Конечно, если после раскрытия скобок получится сходящийся ряд, его сумма будет такой же, как и у ряда со скобками; это следует из доказанного сочетательного свойства.

1.5.7. Переместительное свойство ряда. Ещё больше отличаются поведение конечных сумм и рядов по отношению к переместительному свойству, т.е. к перестановке слагаемых. Если для конечных сумм результат не зависит от порядка слагаемых, то для рядов это не всегда верно. Ряд условно сходится, обозначим его сумму S: . Умножим этот ряд на . Запишем этот ряд так: Почленно сложим этот ряд и ряд S:

. Итак, . Этот ряд отличается от ряда S только порядком слагаемых, однако его сумма в полтора раза больше.

На перестановку членов резко по разному реагируют абсолютно и условно сходящиеся ряды.