 |
|
Достаточный признак сходимости знакочередующегося ряда (признак Лейбница).
Если
1. Последовательность, составленная из модулей членов знакочередующегося ряда, монотонно убывает, т.е. 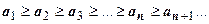 ;
;
2. Выполняется необходимый признак сходимости ряда, т.е. 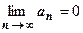 ,
,
то ряд сходится. Его сумма по абсолютной величине не превосходит абсолютную величину первого члена.
Доказательство. Рассмотрим последовательность чётных частичных сумм 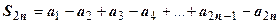 ряда. Представим эту сумму в виде
ряда. Представим эту сумму в виде  . Из первого условия теоремы следует, что суммы в круглых скобках неотрицательны, поэтому последовательность
. Из первого условия теоремы следует, что суммы в круглых скобках неотрицательны, поэтому последовательность  монотонно возрастает с ростом n. С другой стороны,
монотонно возрастает с ростом n. С другой стороны,  , т.е. эта последовательность ограничена сверху величиной
, т.е. эта последовательность ограничена сверху величиной 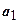 . Следовательно
. Следовательно  . Но для нечётных сумм
. Но для нечётных сумм  , так как по второму условию теоремы
, так как по второму условию теоремы  . Таким образом, частичные суммы имеют предел независимо от их четности или нечётности, т.е. ряд сходится, и его сумма
. Таким образом, частичные суммы имеют предел независимо от их четности или нечётности, т.е. ряд сходится, и его сумма 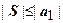 . Знак суммы совпадает со знаком первого члена.
. Знак суммы совпадает со знаком первого члена.
С помощью признака Лейбница доказывается сходимость рядов 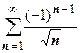 ,
,  .
. 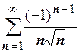 ,
,  и т.д. Третий из этих рядов сходится абсолютно (
и т.д. Третий из этих рядов сходится абсолютно (  сходится), остальные - условно (ряды из модулей членов расходятся). Естественно, существуют знакочередующиеся ряды, для которых условия теоремы Лейбница могут не выполняться; если не выполняется второе условие - необходимый признак сходимости - то ряд заведомо расходится; если не выполняется первое условие, то задача должна решаться с помощью других соображений. Рассмотрим, например, ряд
сходится), остальные - условно (ряды из модулей членов расходятся). Естественно, существуют знакочередующиеся ряды, для которых условия теоремы Лейбница могут не выполняться; если не выполняется второе условие - необходимый признак сходимости - то ряд заведомо расходится; если не выполняется первое условие, то задача должна решаться с помощью других соображений. Рассмотрим, например, ряд 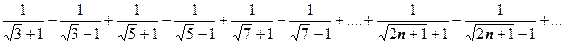 Понятно, что первое условие теоремы Лейбница не выполняется (например,
Понятно, что первое условие теоремы Лейбница не выполняется (например,  ), поэтому эта теорема неприменима и требуется изобрести индивидуальный способ решения этой задачи. Сгруппируем члены попарно:
), поэтому эта теорема неприменима и требуется изобрести индивидуальный способ решения этой задачи. Сгруппируем члены попарно:  Сумма в скобке
Сумма в скобке 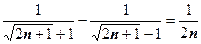 , поэтому последний ряд (со скобками) расходится. Последовательность чётных частичных сумм неограничена, поэтому исходный ряд расходится.
, поэтому последний ряд (со скобками) расходится. Последовательность чётных частичных сумм неограничена, поэтому исходный ряд расходится.
У теоремы Лейбница есть исключительно важный для приложений вывод - вывод о том, что сумма знакочередующегося ряда (или, как говорят, ряда лейбницевского типа) по модулю не больше модуля первого члена: 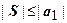 . На нашем уровне нас интересует, в основном, вопрос о сходимости ряда, но при решении практических задач вслед за вопросом о сходимости ряда встаёт вопрос о нахождении его суммы. Основной метод суммирования рядов - вычисление его частичной суммы с количеством слагаемых, обеспечивающим заданную точность. Рассмотрим два примера: найти суммы рядов
. На нашем уровне нас интересует, в основном, вопрос о сходимости ряда, но при решении практических задач вслед за вопросом о сходимости ряда встаёт вопрос о нахождении его суммы. Основной метод суммирования рядов - вычисление его частичной суммы с количеством слагаемых, обеспечивающим заданную точность. Рассмотрим два примера: найти суммы рядов 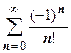 и
и 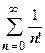 с погрешностью, не превышающей
с погрешностью, не превышающей  . Оба ряда сходятся (пример 1 раздела 1.3.3.Признак сходимости Даламбера). Основная проблема здесь - найти, какое количество n слагаемых надо взять, чтобы частичная сумма
. Оба ряда сходятся (пример 1 раздела 1.3.3.Признак сходимости Даламбера). Основная проблема здесь - найти, какое количество n слагаемых надо взять, чтобы частичная сумма 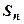 отличалась от суммы ряда S не более, чем на
отличалась от суммы ряда S не более, чем на 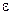 . Так как
. Так как 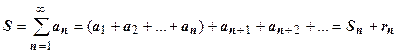 , где
, где 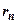 - остаток ряда после n-го члена, и мы хотим принять
- остаток ряда после n-го члена, и мы хотим принять  , то должно быть
, то должно быть 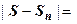
 . И здесь выясняется различие в технике оценки остатка для Лейбницевских рядов с одной стороны и произвольных рядов с другой стороны. Остаток знакочередующегося ряда - тоже знакочередующийся ряд, поэтому он подчиняется выводу теоремы Лейбница:
. И здесь выясняется различие в технике оценки остатка для Лейбницевских рядов с одной стороны и произвольных рядов с другой стороны. Остаток знакочередующегося ряда - тоже знакочередующийся ряд, поэтому он подчиняется выводу теоремы Лейбница: 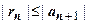 . Другими словами, остаток знакочередующегося ряда по модулю не превосходит первый свой член (или первый отброшенный член ряда). Поэтому для первого из рассматриваемых рядов условие
. Другими словами, остаток знакочередующегося ряда по модулю не превосходит первый свой член (или первый отброшенный член ряда). Поэтому для первого из рассматриваемых рядов условие  сводится к
сводится к 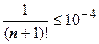 . Подбором убеждаемся, что первое значение n, для которого это условие выполняется, есть n =7 (7!=5040, 8!=40320), поэтому для нахождения суммы ряда
. Подбором убеждаемся, что первое значение n, для которого это условие выполняется, есть n =7 (7!=5040, 8!=40320), поэтому для нахождения суммы ряда 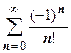 с погрешностью, не превышающей величину
с погрешностью, не превышающей величину  , достаточно взять 7 слагаемых:
, достаточно взять 7 слагаемых: 
(при вычислениях с точностью до 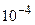 в промежуточных выкладках необходимо удерживать не меньше, чем 5 знаков после запятой. Дальше мы поймём, что вычислено значение
в промежуточных выкладках необходимо удерживать не меньше, чем 5 знаков после запятой. Дальше мы поймём, что вычислено значение  с четырьмя верными цифрами после запятой).
с четырьмя верными цифрами после запятой).
Переходим ко второму ряду. Это знакопостоянный ряд, поэтому единственное, что мы можем сделать - напрямую оценить остаток ряда 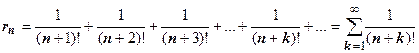 . Пока единственный ряд, для которого мы знаем выражение суммы - геометрическая прогрессия
. Пока единственный ряд, для которого мы знаем выражение суммы - геометрическая прогрессия 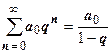 , поэтому надо в той или иной форме свести остаток к геометрической прогрессии. В данном случае это сделать просто:
, поэтому надо в той или иной форме свести остаток к геометрической прогрессии. В данном случае это сделать просто: 
 . Для каждого из слагаемых в круглой скобке верна оценка
. Для каждого из слагаемых в круглой скобке верна оценка 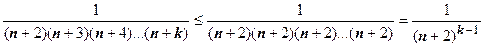 , поэтому
, поэтому 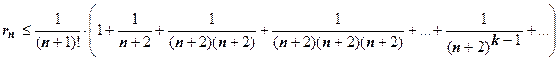 . Ряд в круглых скобках - геометрическая прогрессия со знаменателем
. Ряд в круглых скобках - геометрическая прогрессия со знаменателем  , его сумма равна
, его сумма равна 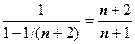 , следовательно,
, следовательно,  . Теперь надо найти такое n, что
. Теперь надо найти такое n, что 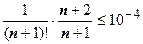 . Перебором различных значений n убеждаемся, что и в этом случае можно взять n =7 (выражение
. Перебором различных значений n убеждаемся, что и в этом случае можно взять n =7 (выражение 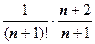 равно 0,0002268 при n = 6 и 0,000028 при n = 8. Итак,
равно 0,0002268 при n = 6 и 0,000028 при n = 8. Итак,  . Это значение числа е с четырьмя верными цифрами после запятой.
. Это значение числа е с четырьмя верными цифрами после запятой.