 |
|
Основные определения.
Пусть дана бесконечная последовательность функций 
.
независимой переменной х, имеющих общую область определения D. Ряд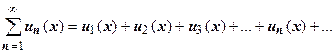 
называется функциональным рядом.
Примеры: 1. 
;
2. 
;
3. 
.
Для каждого значения 
функциональный ряд превращается в числовой ряд, сходящийся или расходящийся. Так, первый из примеров - геометрическая прогрессия со знаменателем х, этот ряд сходится при х=1/2 и расходится при х=2.
Определение. Значение 
, при котором функциональный ряд сходится, называется точкой сходимости функционального ряда. Множество всех точек сходимости функционального ряда называется областью сходимости этого ряда. Область сходимости обозначим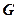 
.
Так, для первого из приведённых примеров область сходимости - интервал (-1, 1); для второго - ряда Дирихле - область сходимости - полуось х>0; третий ряд абсолютно сходится в любой точке х, так как при любом х справедливо 
; следовательно, область сходимости третьего ряда 
).
Для каждого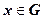 
мы получаем сходящийся числовой ряд, свой для каждого х, поэтому сумма функционального ряда есть функция 
, определённая на области 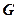. Так, для первого примера, как мы знаем, 
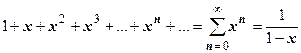, т.е. 
на интервале
(-1, 1); вне этого интервала равенство не имеет места; так, в точке х=2 ряд расходится, а 
. Сумма второго ряда - знаменитая функция Римана 
, определённая на полуоси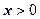 
; эта функция играет важную роль в теории чисел. Сумма третьего ряда, как мы увидим дальше при изучении рядов Фурье, равна функции периода 
, получающаяся в результате периодического повторения функции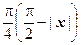 
, определённой на отрезке 
, по всей числовой оси.
Коль скоро мы осознали, что сумма функционального ряда - функция, встаёт вопрос о свойствах этой функции. Так, члены ряда могут иметь свойства непрерывности, дифференцируемости, интегрируемости и т.д. Будет ли обладать этими свойствами сумма ряда? То, что это не праздный вопрос, показывает следующий пример. Пусть 
, 
, 
, 
, …, 
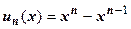, …. Ряд 
состоит из непрерывных членов, найдём его область сходимости и сумму. Частичная сумма ряда 
. Последовательность 
при 
имеет конечный предел только, если 
(это и есть область сходимости ряда), при этом 
Таким образом, для ряда, члены которого - непрерывные функции, мы получили разрывную на области сходимости сумму.
Сумма ряда сохраняет хорошие свойства своих членов в том случае, если ряд сходится равномерно.