 |
|
Необходимый признак сходимости ряда
ЧИСЛОВЫЕ РЯДЫ И БЕСКОНЕЧНЫЕ ПРОИЗВЕДЕНИЯ
Методическая разработка
Составитель:
доцент Путятина Е.Н.
Томск 2012
Одобрено кафедрой общей математики
Зав. кафедрой доцент Е.Н.Путятина
Рассмотрено и утверждено методической комиссией ММФ
Протокол № от ______ 2012 г.
Председатель комиссии О.П.Федорова
В методической разработке изложена теоретическая часть занятий по теме «Числовые ряды и бесконечные произведения » и предложены разнообразные задачи.
Методические указания разработаны для студентов физического факультета, физико-технического факультета, радиофизического факультета дневной формы обучения.
Свойства сходящихся рядов
Определение 1.
Пусть задана последовательность комплексных чисел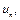 
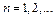. Составленный из этих чисел символ 
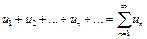называется числовым рядом, а число 
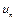- его общим членом.
Определение 2.
Сумма 
первых членов ряда
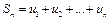называется -той частичной суммой этого ряда, а ряд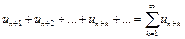 
называется -тым остатком ряда.
Определение 3.
Ряд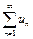 
называется сходящимся, если последовательность его частичных сумм имеет конечный предел: 
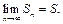Значение 
этого предела называется суммой ряда. Если последовательность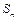 
не имеет предела или 
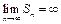, то ряд называется расходящимся.
В примерах 1-6 доказать непосредственно сходимость ряда и найти его сумму.
Пример. 1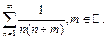 
Так как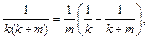 
то
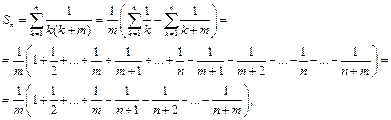
поэтому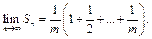 
Пример 2. 
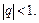
Рассмотрим разность
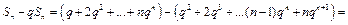
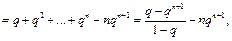откуда находим:
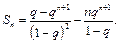Так как при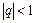 
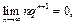то существует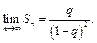 
Пример 3.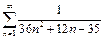 
.
Используя равенство 
получим: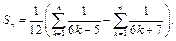 
В первой сумме сделаем замену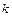 
на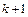 
(т.е. суммирование будет осуществляться от 
до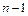 
), а во второй сумме заменим 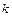на 
, будем иметь:
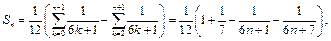
откуда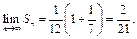 
Пример 4.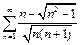 
.
Учитывая, что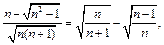 
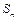для получим:
поэтому существует 
Пример 5. 
.
Частичная сумма ряда равна:
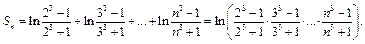
Рассмотрим произведение:
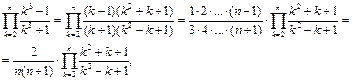
но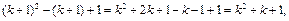 
поэтому
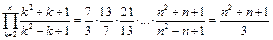и
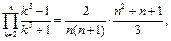откуда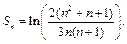 
Следовательно, существует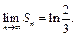 
Пример 6.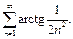 
Используем формулу 
Для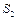 
получим: 
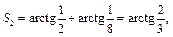для 
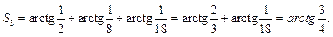
Следуя методу математической индукции, предположим, что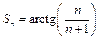 
и докажем, что 
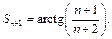Действительно,
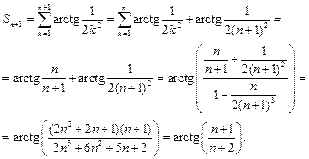
Тогда существует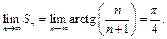 
Необходимый признак сходимости ряда
Если ряд 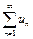сходится, то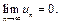 
Этот признак удобно использовать для доказательства расходимости ряда. Ведь если 
не существует или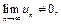 
то ряд расходится.
В примерах 7-10 доказать расходимость ряда, используя необходимый признак сходимости:
Пример 7.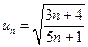 
.
Пример 8. 
.
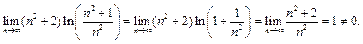
Пример 9.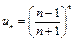 
.
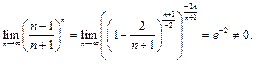
Пример 10.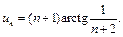 
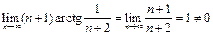(использовали эквивалентность 
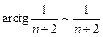при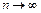 
).