 |
|
Упражнения для самостоятельной работы
1. Доказать непосредственно сходимость следующих рядов и найти их суммы:
1) 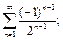 2)
2)  3)
3) 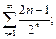 4)
4) 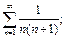
4) 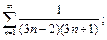 5)
5) 
6) 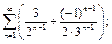 7)
7) 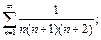 8)
8) 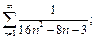
9) 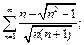 10)
10) 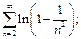 11)
11) 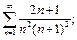
12)  13)
13) 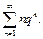
2.Доказать расходимость ряда, используя необходимый признак сходимости:
1) 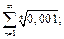 2)
2)  3)
3) 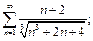
4) 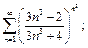 5)
5)  6)
6) 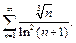
3.Пользуясь критерием Коши, доказать сходимость следующих рядов:
1) 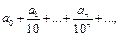

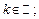
2) 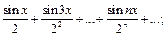
3) 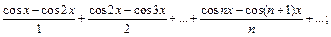
4) 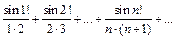 .
.
4.Пользуясь критерием Коши, доказать расходимость следующих рядов:
1) 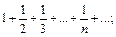 2)
2) 
3) 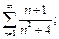 4)
4) 
§2. Ряды с неотрицательными членами
Рассмотрим ряд 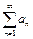 , где
, где  Для исследования данного ряда на сходимость существует достаточно много эффективных признаков.
Для исследования данного ряда на сходимость существует достаточно много эффективных признаков.
Критерий сходимости ряда с неотрицательными членами
Ряд 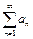 с неотрицательными членами сходится тогда и только тогда, когда последовательность его частичных сумм ограничена сверху:
с неотрицательными членами сходится тогда и только тогда, когда последовательность его частичных сумм ограничена сверху: 
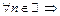
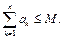
Пример 1. Исследовать на сходимость ряд 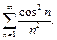
Так как 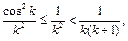 то
то

поэтому ряд сходится.
Признаки сравнения
1. Если для всех  выполняется неравенство
выполняется неравенство  то из сходимости ряда
то из сходимости ряда 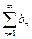 следует сходимость ряда
следует сходимость ряда 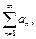 а из расходимости ряда
а из расходимости ряда 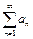 следует расходимость ряда
следует расходимость ряда 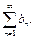
2. Если 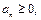
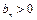 для всех
для всех  и существует конечный предел
и существует конечный предел 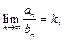 то: а) при
то: а) при 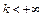 из сходимости ряда
из сходимости ряда 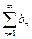 следует сходимость ряда
следует сходимость ряда 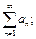
б) при 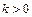 из расходимости ряда
из расходимости ряда 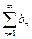 следует
следует
расходимость ряда 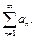 При
При 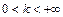 ряды
ряды
сходятся либо расходятся одновременно.
Применение признаков сравнения предполагает наличие рядов, о поведении которых заранее известно и которые могут использоваться для сравнения. Одним из таких рядов является обобщённый гармонический ряд  сходящийся при
сходящийся при 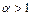 и расходящийся, если
и расходящийся, если  Исследование на сходимость обобщённого гармонического ряда будет проведено в примере 14.
Исследование на сходимость обобщённого гармонического ряда будет проведено в примере 14.
В примерах 2-8 исследовать ряды на сходимость, пользуясь признаками сравнения:
Пример 2. 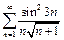 .
.
Для 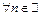 выполнено неравенство:
выполнено неравенство: 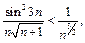 а ряд
а ряд 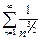 сходится, следовательно, сходится и исходный ряд.
сходится, следовательно, сходится и исходный ряд.
Пример 3. 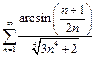 .
.
Так как 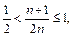 то
то 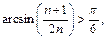 поэтому для всех
поэтому для всех  справедливо неравенство:
справедливо неравенство:
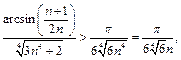 а из расходимости ряда
а из расходимости ряда 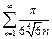 следует расходимость данного ряда.
следует расходимость данного ряда.
Пример 4. 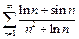 .
.
Для 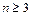 имеет место неравенство:
имеет место неравенство: 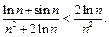
Покажем, что ряд 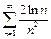 сходится. Для сравнения используем сходящийся ряд
сходится. Для сравнения используем сходящийся ряд 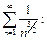
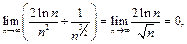 поэтому согласно второму признаку сравнения ряд
поэтому согласно второму признаку сравнения ряд 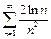 сходится.
сходится.
Следовательно, исходный ряд сходится по первому
признаку сравнения.
Пример 5. 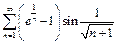
Общий член данного ряда при 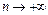 эквивалентен
эквивалентен 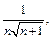 а ряд
а ряд 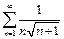 сходится, поэтому сходится и исходный ряд.
сходится, поэтому сходится и исходный ряд.
Пример 6. 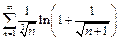 .
.
Так как 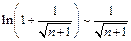 при
при 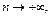 то
то 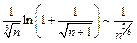 при
при 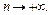 Но ряд
Но ряд  расходится, следовательно, расходится и исходный ряд.
расходится, следовательно, расходится и исходный ряд.
Пример 7. 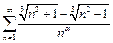 .
.
Преобразуем общий член ряда:
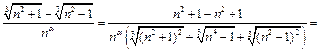
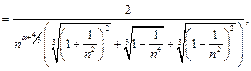 откуда следует, что
откуда следует, что 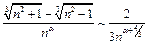 при
при 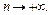 Ряд
Ряд  сходится, если
сходится, если  т.е.
т.е. 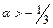 и расходится, если
и расходится, если 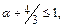 т.е.
т.е. 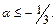 Итак, данный ряд сходится при
Итак, данный ряд сходится при 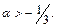
Пример 8. 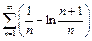 .
.
Воспользуемся известным неравенством: 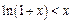 , если
, если 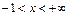 и
и 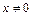 . Тогда
. Тогда  , с другой стороны:
, с другой стороны:
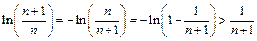 .
.
Поэтому 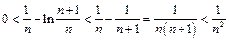 .
.
Так как ряд 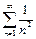 сходится, то сходится и данный ряд.
сходится, то сходится и данный ряд.
Замечание: для доказательства использованного неравенства можно исследовать на экстремум функцию  и показать, что
и показать, что 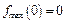 .
.
Признак Даламбера
Если для ряда 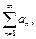
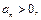
 существуют такое число
существуют такое число 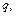
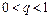 и такой номер
и такой номер 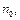 что для всех
что для всех  выполняется неравенство
выполняется неравенство 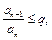 то этот ряд сходится, если же для всех
то этот ряд сходится, если же для всех  имеет место неравенство
имеет место неравенство 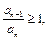 то ряд расходится.
то ряд расходится.
Следствие. Если существует 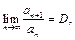 то при
то при 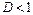 ряд
ряд 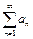 сходится, а при
сходится, а при  расходится. При
расходится. При 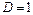 признак Даламбера ответа не даёт.
признак Даламбера ответа не даёт.
В примерах 9-11 исследовать ряды на сходимость с помощью признака Даламбера:
Пример 9. 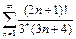 .
.
Будем использовать следствие: 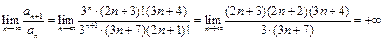 ,
,
следовательно, ряд расходится.
Пример 10. 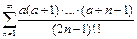 ,
, 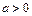 .
.
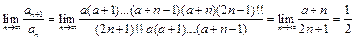 - исходный ряд сходится.
- исходный ряд сходится.
Пример 11. 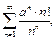
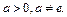

Если 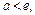 то ряд сходится, если же
то ряд сходится, если же 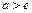 - расходится.
- расходится.
Признак Коши
Если для ряда 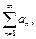
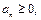
 существуют такие число
существуют такие число 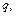
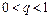 и номер
и номер 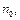 что для всех
что для всех  выполняется неравенство
выполняется неравенство  то этот ряд сходится, если же для всех
то этот ряд сходится, если же для всех  имеет место неравенство
имеет место неравенство 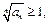 то ряд расходится.
то ряд расходится.
Следствие.Если существует 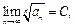 то при
то при 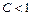 ряд сходится, а при
ряд сходится, а при 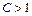 ряд расходится. При
ряд расходится. При  признак Коши ответа не даёт.
признак Коши ответа не даёт.
В примерах 12-14 исследовать ряды на сходимость с помощью признака Коши:
Пример 12. 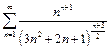 .
.
Учитывая, что 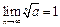 для
для 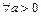 и
и 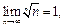 будем иметь:
будем иметь:
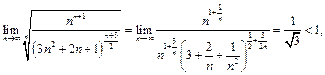 поэтому ряд сходится.
поэтому ряд сходится.
Пример 13. 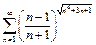 .
.
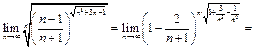
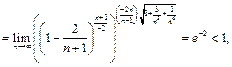 следовательно, ряд сходится.
следовательно, ряд сходится.
Пример 14. 

 для
для  поэтому ряд сходится.
поэтому ряд сходится.
Признак Коши является более сильным, чем признак Даламбера: из существования  следует существование
следует существование 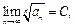 причём
причём 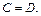 Обратное неверно: например, для ряда
Обратное неверно: например, для ряда 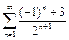 величина
величина 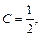 а
а 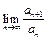 не существует. Так что если для какого-то ряда
не существует. Так что если для какого-то ряда 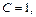 то нет смысла использовать признак Даламбера, он ответа не даст.
то нет смысла использовать признак Даламбера, он ответа не даст.