 |
|
Критерий Коши сходимости ряда
Ряд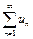 
сходится тогда и только тогда, когда для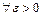 
Пример 11. Пользуясь критерием Коши, доказать сходимость ряда 
Рассмотрим сумму:
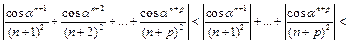
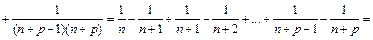
если 
Таким образом, для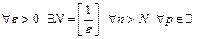 
Если условие Коши не выполняется, т.е. 
, но 
то ряд расходится.
Пример 12. Доказать, используя отрицание условия Коши, что ряд 
расходится.
Рассмотрим сумму:
Пусть 
тогда
Следовательно, 
, 
и 
такие, что будет выполняться неравенство: 
Для случая комплексных 
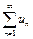сходимость ряда эквивалентна одновременной сходимости вещественных рядов 
и 
ибо 
Поэтому исследование на сходимость рядов с комплексными членами, как правило, сводится к рассмотрению рядов с вещественными членами. Однако иногда для нахождения суммы вещественного ряда можно использовать ряды с комплексными членами. Приведём примеры.
В примерах 13-15 найти сумму ряда:
Пример 13.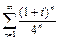 
.
Сумма геометрической прогрессии со знаменателем 
где 
равна:
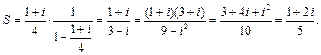
Пример 14. 
.
Для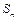 
имеем:
поэтому
Пример 15. 
.
Воспользуемся формулой Эйлера:
тогда
- сумма 
членов геометрической прогрессии со знаменателем 
для которого 
Поэтому
Выделяя вещественную и мнимую части, получим:
Для сходящихся рядов справедливы следующие важные теоремы:
1. Пусть 
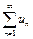. Если ряд сходится, то ряд 
также сходится и его сумма равна: 
(Другими словами, числовой множитель можно выносить за скобку и в случае бесконечного числа слагаемых).
2. Два сходящихся ряда 
можно складывать или вычитать почленно, так что ряд 
также сходится и его сумма равна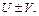 
Замечание к теоремам 1,2:множество сходящихся рядов представляет собой линейное пространство.
3. Если ряд 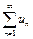сходится, то сходится и любой из его остатков и обратно, из сходимости остатка ряда вытекает сходимость исходного ряда.
4. Пусть 
возрастающая последовательность натуральных чисел. Если ряд 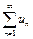сходится, то всегда сходится ряд 
имеющий ту же сумму, что и исходный ряд. Иными словами, сходящийся ряд обладает сочетательным свойством.
Замечание к теореме 4: обратное утверждение неверно. Если дан сходящийся ряд, члены которого каждый в отдельности представляет собой сумму конечного числа слагаемых, то, опустив скобки, мы получим новый ряд, который может оказаться и расходящимся. Например, ряды 
или 
сходятся, а после удаления скобок получаем расходящийся ряд: 
. Если же, опустив скобки, мы всё-таки получаем сходящийся ряд, то его сумма будет такой же, что и у ряда 
Внимание! В случае, когда все слагаемые в ряде 
внутри одних и тех же скобок одного знака, из сходимости ряда будет следовать и сходимость ряда 
полученного путём отбрасывания скобок. Этим важным свойством можно воспользоваться при решении некоторых сложных задач.