 |
|
Абсолютная и условная сходимость
Определение 1. Ряд 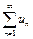 называется абсолютно сходящимся, если сходится ряд
называется абсолютно сходящимся, если сходится ряд 
При исследовании рядов на абсолютную сходимость к ряду 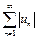 могут быть применены все признаки сходимости для положительных рядов.
могут быть применены все признаки сходимости для положительных рядов.
Имеют место следующие важные теоремы:
1. абсолютно сходящийся ряд сходится;
2. абсолютно сходящийся ряд обладает переместительным свойством;
3. если ряды  и
и  сходятся абсолютно, то ряд, составленный из всевозможных произведений
сходятся абсолютно, то ряд, составленный из всевозможных произведений  занумерованных в каком угодно порядке, также сходится абсолютно и его сумма равна
занумерованных в каком угодно порядке, также сходится абсолютно и его сумма равна 
В примерах 1-4 доказать абсолютную сходимость ряда 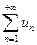 :
:
Пример 1.  .
.
Ряд 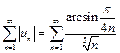 легко исследовать на сходимость по признаку сравнения с рядом
легко исследовать на сходимость по признаку сравнения с рядом  , который сходится:
, который сходится: 
Пример 2.  .
.
Для доказательства сходимости ряда 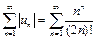 применим признак Даламбера:
применим признак Даламбера:

Следовательно, ряд 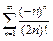 сходится абсолютно.
сходится абсолютно.
Пример 3. 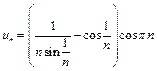 .
.
Так как 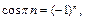 то
то  Воспользуемся методом выделения главной части:
Воспользуемся методом выделения главной части:
 поэтому
поэтому

 следовательно,
следовательно,

Таким образом,  при
при  а ряд
а ряд  сходится, поэтому исходный ряд сходится абсолютно.
сходится, поэтому исходный ряд сходится абсолютно.
Пример 4.  .
.
Так как  то
то
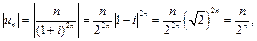 а ряд
а ряд  сходится, что доказано в примере 2 § 1 для более общего случая
сходится, что доказано в примере 2 § 1 для более общего случая 

 Итак, данный ряд сходится абсолютно.
Итак, данный ряд сходится абсолютно.
Определение 2. Ряд 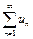 называется условно сходящимся, если этот ряд сходится, а ряд
называется условно сходящимся, если этот ряд сходится, а ряд 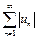 расходится.
расходится.
Теорема Римана.
Если ряд 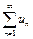 ,
,  сходится условно, то каково бы ни было наперёд заданное число
сходится условно, то каково бы ни было наперёд заданное число 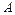 (включая
(включая  ), можно так переставить члены этого ряда, чтобы преобразованный ряд сходился к числу
), можно так переставить члены этого ряда, чтобы преобразованный ряд сходился к числу 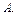
Для исследования рядов на сходимость существует несколько достаточных признаков. Рассмотрим их.
Определение 3. Ряд вида  где
где  либо
либо  для
для 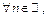 называется знакочередующимся.
называется знакочередующимся.
Признак Лейбница.
Знакочередующийся ряд сходится, если: а) 
 б)
б) 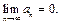
В этом случае для остатка ряда  имеем оценку:
имеем оценку: 
В примерах 5-7 исследовать на сходимость знакочередующиеся ряды.
Пример 5.  .
.
Согласно признаку Лейбница требуется доказать, что  и
и 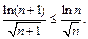 Правило Лопиталя приводит
Правило Лопиталя приводит
к результату:  Обозначив
Обозначив  докажем, что
докажем, что  убывает:
убывает:
 если
если  т.е.
т.е.  Следовательно, последовательность
Следовательно, последовательность  монотонно убывает для
монотонно убывает для  а исходный ряд сходится по признаку Лейбница.
а исходный ряд сходится по признаку Лейбница.
Пример 6.  .
.
Так как  при
при  то
то  и последовательность
и последовательность  монотонно убывает, поэтому данный ряд сходится по признаку Лейбница.
монотонно убывает, поэтому данный ряд сходится по признаку Лейбница.
Пример 7. 
Преобразуем общий член ряда:

Ряд  сходится по признаку Лейбница:
сходится по признаку Лейбница:  последовательность
последовательность  монотонно убывает (
монотонно убывает ( 
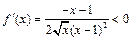 для
для  ); а ряд
); а ряд  с положительными членами расходится. Следовательно, исходный ряд также расходится.
с положительными членами расходится. Следовательно, исходный ряд также расходится.
Отметим, что если данный ряд сравнить со сходящимся рядом  то отношение их общих членов стремится к 1 (т.е.
то отношение их общих членов стремится к 1 (т.е.  при
при 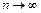 - последовательность членов данного расходящегося ряда эквивалентна последовательности членов сходящегося ряда). Внимание! Делать вывод о сходимости или расходимости ряда
- последовательность членов данного расходящегося ряда эквивалентна последовательности членов сходящегося ряда). Внимание! Делать вывод о сходимости или расходимости ряда 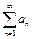 по поведению ряда
по поведению ряда 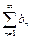 , где
, где 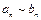 при
при 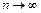 возможно только для рядов с положительными членами!!
возможно только для рядов с положительными членами!!
Убедимся в том, что каждое из трёх условий в признаке Лейбница является существенным. Во-первых, существенность условия  вытекает из необходимого признака сходимости рядов. Во-вторых, в признаке Лейбница нельзя отбросить условие знакочередуемости. Для иллюстрации этого рассмотрим ряд:
вытекает из необходимого признака сходимости рядов. Во-вторых, в признаке Лейбница нельзя отбросить условие знакочередуемости. Для иллюстрации этого рассмотрим ряд:  . Абсолютные величины членов ряда не возрастают и стремятся к нулю, но его частичные суммы
. Абсолютные величины членов ряда не возрастают и стремятся к нулю, но его частичные суммы  равны
равны  а остальные частичные суммы принимают промежуточные значения (между нулём и единицей), поэтому ряд расходится. То, что не является лишним требование монотонности, демонстрируют уже рассмотренный в примере 7 ряд
а остальные частичные суммы принимают промежуточные значения (между нулём и единицей), поэтому ряд расходится. То, что не является лишним требование монотонности, демонстрируют уже рассмотренный в примере 7 ряд  а также следующий ряд:
а также следующий ряд:  .
.
Сумма  его членов равна:
его членов равна:
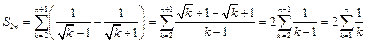 -
-
- удвоенной сумме  членов расходящегося гармонического ряда. Следовательно,
членов расходящегося гармонического ряда. Следовательно,  Здесь налицо нарушение монотонности при переходе от члена
Здесь налицо нарушение монотонности при переходе от члена
 к члену
к члену  (их отношение
(их отношение  меньше 1).
меньше 1).
Пример 8. Исследовать на сходимость ряд 
В данном ряде за группой отрицательных членов следует группа положительных и т.д. Объединим каждую такую группу членов одного знака в один член, тогда получим ряд:  который будем исследовать на сходимость по признаку Лейбница. Так как
который будем исследовать на сходимость по признаку Лейбница. Так как
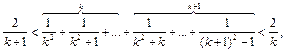 то члены рассматриваемого ряда при
то члены рассматриваемого ряда при  будут стремиться к нулю, монотонно убывая по абсолютной величине. Поэтому ряд сходится, а вместе с ним будет сходиться и исходный ряд (см. замечание к теореме о сочетательном свойстве рядов в § 1).
будут стремиться к нулю, монотонно убывая по абсолютной величине. Поэтому ряд сходится, а вместе с ним будет сходиться и исходный ряд (см. замечание к теореме о сочетательном свойстве рядов в § 1).
Для общего случая знакопеременных рядов либо для рядов с комплексными членами справедливы признаки Абеля и Дирихле.
Признак Абеля. Ряд  где
где 

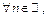 сходится, если: а) ряд
сходится, если: а) ряд 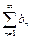 сходится; б) последовательность
сходится; б) последовательность  монотонна и ограничена.
монотонна и ограничена.
Признак Дирихле. Ряд 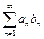 , где
, где 

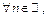 сходится, если: а) частичные суммы ряда
сходится, если: а) частичные суммы ряда 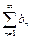 в совокупности ограничены, т.е.
в совокупности ограничены, т.е. 
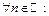
 б) последовательность
б) последовательность  при
при 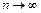 монотонно стремится к нулю.
монотонно стремится к нулю.
Отметим: 1) признак Лейбница является частным случаем признака Дирихле при  2) признак Абеля вытекает из признака Дирихле, ведь из предположений Абеля следует, что существует
2) признак Абеля вытекает из признака Дирихле, ведь из предположений Абеля следует, что существует  а тогда
а тогда  - здесь второй ряд сходится по предположению а) признака Абеля, а к первому можно применить признак Дирихле.
- здесь второй ряд сходится по предположению а) признака Абеля, а к первому можно применить признак Дирихле.
В примерах 9-12 исследовать ряды на сходимость:
Пример 9.  .
.
Применим признак Абеля. Ряд  сходится по признаку Лейбница, а последовательность
сходится по признаку Лейбница, а последовательность 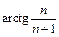 монотонно возрастает и ограничена:
монотонно возрастает и ограничена: 
поэтому данный ряд сходится.
Пример 10. 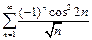 .
.
Преобразуем общий член ряда: 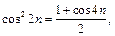 поэтому
поэтому  . Ряд
. Ряд 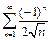 сходится по признаку Лейбница, а к ряду
сходится по признаку Лейбница, а к ряду 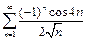 применим признак Дирихле:
применим признак Дирихле:  при
при 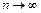 монотонно, а
монотонно, а 
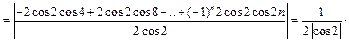
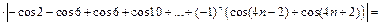

Следовательно, ряд 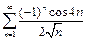 сходится, а значит сходится и исходный ряд.
сходится, а значит сходится и исходный ряд.
Пример 11.  .
.
Используя признак Абеля, покажем, что ряд  сходится, а последовательность
сходится, а последовательность  монотонна и ограничена. Для доказательства сходимости ряда применим признак Дирихле: последовательность
монотонна и ограничена. Для доказательства сходимости ряда применим признак Дирихле: последовательность  монотонно при
монотонно при  а частичные суммы ряда
а частичные суммы ряда  в совокупности ограничены:
в совокупности ограничены:  так как
так как  а
а  поэтому ряд
поэтому ряд  сходится. Последовательность
сходится. Последовательность  монотонно возрастает и ограничена сверху числом
монотонно возрастает и ограничена сверху числом  Следовательно, исходный ряд сходится.
Следовательно, исходный ряд сходится.
Пример 12.  .
.
К данному ряду также применим признак Абеля. Докажем, следуя признаку Дирихле, что ряд  сходится, а последовательность
сходится, а последовательность  монотонна и ограничена. Действительно, частичные суммы ряда
монотонна и ограничена. Действительно, частичные суммы ряда  ограничены в совокупности:
ограничены в совокупности:


 а последовательность
а последовательность
 монотонно при
монотонно при  поэтому ряд
поэтому ряд 
сходится. Последовательность  монотонно возрастает и ограничена сверху:
монотонно возрастает и ограничена сверху: 
Следовательно, исходный ряд сходится по признаку Абеля.
В примерах 13-15 исследовать ряды на абсолютную и условную сходимость.
Пример 13.  .
.
Преобразуем общий член ряда, используя формулу Тейлора:
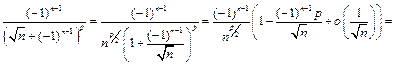

Ряд 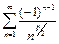 сходится по признаку Лейбница при
сходится по признаку Лейбница при  а обобщённый гармонический ряд
а обобщённый гармонический ряд  сходится при
сходится при  Следовательно, данный ряд сходится при
Следовательно, данный ряд сходится при 
Для исследования ряда на абсолютную сходимость используем оценку:

Ряды  и
и  по признаку сравнения с рядом
по признаку сравнения с рядом  сходятся при
сходятся при  и расходятся при
и расходятся при  Поэтому из сходимости ряда
Поэтому из сходимости ряда  при
при  следует сходимость рассматриваемого ряда, а из расходимости ряда
следует сходимость рассматриваемого ряда, а из расходимости ряда  при
при  следует расходимость ряда
следует расходимость ряда  Итак, данный ряд сходится абсолютно при
Итак, данный ряд сходится абсолютно при  и условно при
и условно при 
Пример 14.  .
.
Простейшая оценка  не даёт информации о поведении ряда
не даёт информации о поведении ряда  Будем использовать признак Абеля. Положим:
Будем использовать признак Абеля. Положим: 
 Ряд
Ряд  сходится условно по признаку Дирихле:
сходится условно по признаку Дирихле:  а
а  при
при  монотонно стремится к нулю. Последовательность
монотонно стремится к нулю. Последовательность  монотонна и ограничена:
монотонна и ограничена: 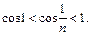 Следовательно, данный ряд сходится по признаку Абеля.
Следовательно, данный ряд сходится по признаку Абеля.
Расходимость ряда  следует из неравенства:
следует из неравенства: 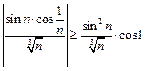 и расходимости ряда
и расходимости ряда  ведь ряд
ведь ряд  расходится, а ряд
расходится, а ряд  сходится по признаку Дирихле:
сходится по признаку Дирихле:  монотонно при
монотонно при  а
а  Следовательно, данный ряд сходится условно.
Следовательно, данный ряд сходится условно.
Пример 15. 
Так как при  необходимый признак сходимости не выполняется, то ряд расходится.
необходимый признак сходимости не выполняется, то ряд расходится.
Для исследования на сходимость применим признак Лейбница: 1) из очевидного при 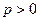 неравенства
неравенства  следует монотонное убывание последовательности
следует монотонное убывание последовательности  ; 2) условие
; 2) условие  вытекает из неравенства
вытекает из неравенства 
по принципу двустороннего ограничения также при 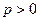 . Следовательно, при
. Следовательно, при 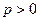 данный ряд сходится.
данный ряд сходится.
Для ряда  с использованием формулы Тейлора будем иметь:
с использованием формулы Тейлора будем иметь:
 , где
, где  , поэтому по признаку Гаусса ряд
, поэтому по признаку Гаусса ряд  сходится при
сходится при  и расходится при
и расходится при 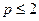 .
.
Тогда исходный ряд сходится абсолютно при  , а при
, а при  сходится условно.
сходится условно.