 |
|
Интегральный признак Коши-Маклорена
Пусть функция  , определённая для
, определённая для  непрерывная, положительная и монотонно убывающая. Тогда, если функция
непрерывная, положительная и монотонно убывающая. Тогда, если функция  при
при  имеет конечный предел, то ряд
имеет конечный предел, то ряд  сходится. Если же
сходится. Если же  то ряд
то ряд  расходится.
расходится.
Пользуясь интегральным признаком, исследовать на сходимость ряды в примерах 15-16.
Пример 15.  .
.
Для  первообразная имеет вид:
первообразная имеет вид:
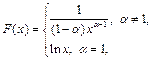 поэтому при
поэтому при 
 , и ряд
, и ряд  расходится, если же
расходится, если же  то
то  , и ряд сходится.
, и ряд сходится.
Пример 16. 
Если  то
то  поэтому согласно результатам предыдущего примера данный ряд сходится при
поэтому согласно результатам предыдущего примера данный ряд сходится при  и расходится при
и расходится при 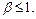
Интегральный признак Коши-Маклорена является, как видно из его формулировки, необходимым и достаточным признаком. Это значит, что он устанавливает сходимость любого сходящегося ряда и расходимость любого расходящегося ряда из сферы своей применимости. Однако при изучении рядов ограничиться одним только интегральным признаком сходимости нельзя, поскольку применение его не всегда возможно.
Рассмотрим два признака, являющихся и удобными в обращении, и значительно более чувствительными, чем признаки Коши и Даламбера.
Признак Раабе
Если для ряда 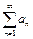 ,
, 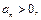
 существует
существует  , то при
, то при  ряд сходится, а при
ряд сходится, а при  расходится. При
расходится. При  признак ответа не даёт.
признак ответа не даёт.
В примерах 17-19, пользуясь признаком Рабе, исследовать ряды на сходимость.
Пример 17.  .
.
Так как  то
то  и признак Даламбера ответа не даёт. Однако
и признак Даламбера ответа не даёт. Однако  и ряд расходится.
и ряд расходится.
Пример 18.  .
.
 - данный ряд сходится.
- данный ряд сходится.
Пример 19.  ,
, 

следовательно, ряд сходится, если  и расходится, если
и расходится, если 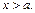 При
При 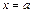 признак Раабе не даёт ответа.
признак Раабе не даёт ответа.
Признак Гаусса
Если для ряда 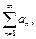
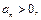
 отношение
отношение  может быть представлено в виде:
может быть представлено в виде: 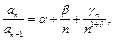 где
где 
 то: а) при
то: а) при 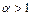 ряд сходится, а при
ряд сходится, а при  расходится; б) при
расходится; б) при 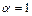 ряд сходится в случае, когда
ряд сходится в случае, когда  и расходится, если
и расходится, если 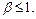
Исследовать на сходимость ряды, используя признак Гаусса:
Пример 20.  .
.
В примере 10 был исследован ряд 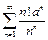 ,
,  и на основании признака Даламбера показано, что ряд сходится при
и на основании признака Даламбера показано, что ряд сходится при  и расходится при
и расходится при  В случае
В случае 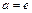 признак Даламбера неприменим -
признак Даламбера неприменим -  Воспользуемся признаком Гаусса:
Воспользуемся признаком Гаусса:
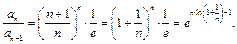 Так как
Так как
 то
то 
Итак, 
 и ряд расходится.
и ряд расходится.
Пример 21. 
 .
. 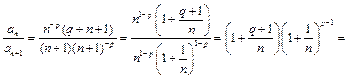


Следовательно, 
 , и ряд сходится, если
, и ряд сходится, если  и расходится при
и расходится при 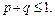
Пример 22. 

Так как  и
и 
 где
где  то
то


Если 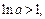 т.е.
т.е. 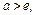 то ряд сходится. Если же
то ряд сходится. Если же  то ряд расходится.
то ряд расходится.
Как следует из примеров 19-21, применение признака Гаусса требует порой использования формулы Тейлора. Метод выделения главной части при исследовании на сходимость положительных рядов является достаточно эффективным. Если с помощью формулы Тейлора удаётся получить асимптотическую формулу вида  при
при 
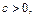 то при
то при 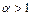 ряд
ряд 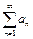 сходится, а при
сходится, а при  расходится.
расходится.
В примерах 23-25 исследовать ряды на сходимость, получив асимптотическую формулу вида  при
при 
Пример 23. 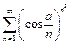 .
. 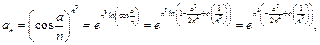
поэтому  при
при  Но ряд
Но ряд  сходится для
сходится для 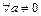 по признаку сравнения с рядом
по признаку сравнения с рядом 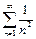 :
:  Следовательно, при
Следовательно, при  исходный ряд сходится, если же
исходный ряд сходится, если же 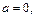 то
то 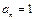 и ряд расходится.
и ряд расходится.
Пример 24.  .
.
Отметим, что при  данный ряд расходится, ибо для него не выполнен необходимый признак сходимости ряда. Пусть
данный ряд расходится, ибо для него не выполнен необходимый признак сходимости ряда. Пусть 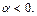 Тогда
Тогда  при
при 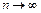 (так как
(так как  при
при 
 ). Исследуем на сходимость ряд
). Исследуем на сходимость ряд 
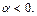 Если
Если  то данный ряд сходится по второму признаку сравнения с рядом
то данный ряд сходится по второму признаку сравнения с рядом  , где
, где  и такое, что
и такое, что 
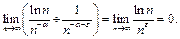 Если же
Если же  то ряд расходится по первому признаку сравнения:
то ряд расходится по первому признаку сравнения:  Таким образом, исходный ряд сходится, если
Таким образом, исходный ряд сходится, если 
Пример 25.  .
.
Учитывая, что 
 получим:
получим:

 поэтому
поэтому
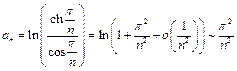 при
при  а это значит, что данный ряд сходится.
а это значит, что данный ряд сходится.