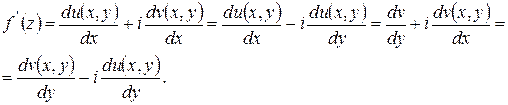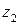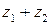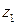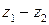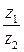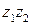 |
|
Контрольная работа №2
Задание 5
Комплексные числа и действия над ними
1. Цель работы
Научиться оперировать с комплексными числами и отображать их на плоскости.
2. Основные теоретические положения
См. раздел 2.1 (с.36, 37) УМК и раздел 3 Учебного пособия (с.19-23).
3. Порядок выполнения работы
Пример 1.
Найти сумму и разность чисел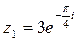 
и 
.
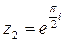○Числа даны в показательной форме, однако, операции алгебраического суммирования удобнее производить над числами, записанными в алгебраической форме, т.к. достаточно соответствующие действия выполнить отдельно для вещественных и отдельно для мнимых частей чисел, т.е.
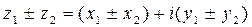
| (5) |
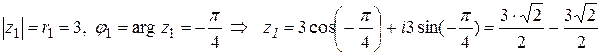i,
, 
.
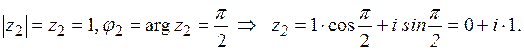
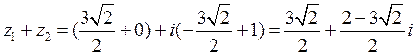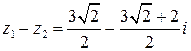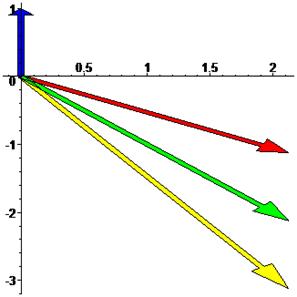
Учитывая, что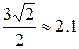 
, построим все числа на рис. 1.●
|
| ||||
| ||||
|
Рис. 1
Пример 2.
Найти произведение и частное чисел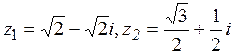 
.
○Находя z1×z2 поступим с числами, как с обычными алгебраическими многочленами, учитывая, что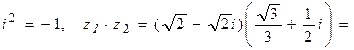 
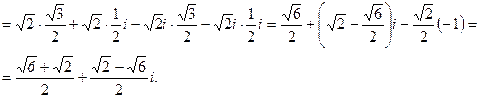
Чтобы найти частное, следует освободиться в знаменателе от комплексного числа, для этого и числитель и знаменатель нужно умножить на число, сопряженное знаменателю.
На рис.2 представлены все числа.●
|
|
|
|
Рис.2
Задание 6
Вычисление производных функции комплексного переменного
1. Цель работы
Научиться вычислять производные от ФКП.
2. Основные теоретические положения
См. раздел 2.2 УМК (с.37-39) и раздел 4.2 Учебного пособия (с.26-29).
Пример.
Вычислить производную функции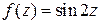 
в точке z0=πi.
○Для того чтобы функция была аналитической в некоторой области необходимо и достаточно, чтобы её вещественная и мнимая части были определены и непрерывны в этой области и удовлетворяли условиям Коши- Римана, т.е.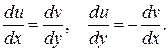 
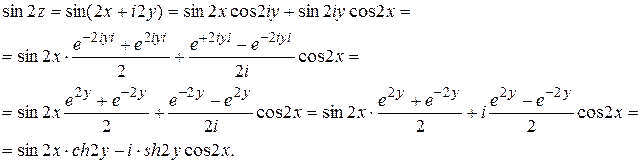
(воспользовались формулами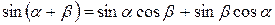 
;
).
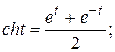
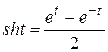Таким образом, u(x,y)=sin2x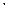 
ch2y; v(x,y)=-sh2y 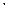cos2x. Обе функции определены и непрерывны на всей комплексной плоскости. Осталось показать, что они удовлетворяют условиям Коши- Римана. Для этого нужно найти частные производные u(x,y) и v(x,y).
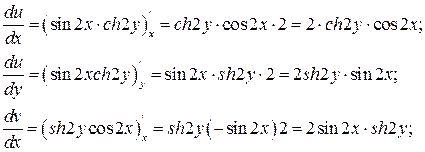
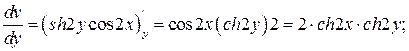
Таким образом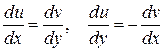 
, т.е. условия Коши- Римана выполнены. Следовательно, рассматриваемая функция аналитическая по всей числовой плоскости. Производную можно найти, воспользовавшись одной из формул:
