Главная | Обратная связь

Однако, имея в виду, что для аналитических функций справедливы все правила и формулы дифференцирования функции действительного аргумента, можно избежать применения этих формул.

●

 

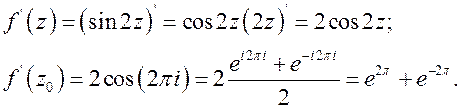Задание 7

Интегрирование функции комплексного переменного

 

1. Цель работы

 

Научиться определять тип особых точек и вычислять интегралы от функций комплексного переменного с помощью вычетов.

 

2. Основные теоретические положения

 

См. раздел 2.4 УМК (с.41-44) и раздел 6 (с.36-49) Учебного пособия.

 

Пример 1.

Вычислить интеграл .

(Обход контура в положительном направлении).

○Контур интегрирования – окружность радиусом 2 и центром в точке (-3;0) (рис. 1).

 

Здесь подынтегральная функция аналитическая везде, кроме точек х₁=0; х₂=2i; x₃=-2i. Эти точки лежат вне области, ограниченной контуром интегрирования, следовательно, можно применить интегральную теорему Коши, согласно которой, интеграл по контору,

Рис. 1.

 

ограничивающему область аналитичности функции, равен нулю. Таким образом, .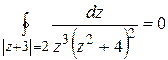

В тех случаях, когда в области, ограниченной контуром интегрирования, подынтегральная функция имеет особые точки, для вычисления интеграла применяется теорема Коши о вычетах: , при условии, что f(z) непрерывна на границе интегрирования и аналитическая всюду внутри области, кроме конечного числа особых точек z₁, z₂,…, z_n.

Таким образом, для того чтобы вычислить интеграл по замкнутому контуру, необходимо определить особые точки, принадлежащие области, ограниченной контуром интегрирования, и вычислить вычеты в этих точках (resf(z_k)).

Напомним, что изолированные особые точки могут быть устранимыми, полюсами (простыми и порядка m), а также существенно особыми точками.

Особая точка называется устранимой особой точкой, если существует конечный предел , вычет в этой точке resf(z₀)=0.

Особая точка называется полюсом, если 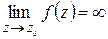. Порядок полюса определяется кратностью нуля z₀ функции .

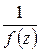Вычет в простом полюсе вычисляется по формуле

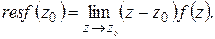(1)

Вычет в полюсе порядка m вычисляется по формуле

(2)

В частности при m=1 получим предыдущую формулу (имеем в виду, что 0!=1, производная нулевого порядка – сама функция); при m=2 (для полюса второго порядка)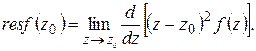

Особая точка называется существенно особой точкой, если 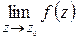не существует. В этом случае resf(z₀) определяется, как коэффициент a_-1при минус первой степени при (z-z₀) разложения f(z) в ряд Лорана.●

Пример 2.

Найти особые точки функции . ○Эта функция имеет две особые точк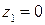и и . Найдем пределы функции в этих точках.

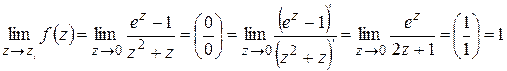- предел конечный, следовательно, z₁=0 – устранимая особая точка. Вычет в ней равен 0. 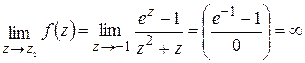, следовательно, точка – полюс. Поскольку –1 простой ноль функции 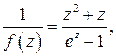точка является простым полюсом. Вычет в ней .

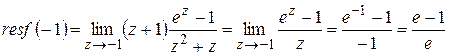Замечание. При вычислении пределов использовалось правило Лопиталя.●

Пример 3.

Найти особые точки функции 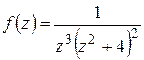, определить их тип, найти вычет в каждой из них.

○f(z) имеет три особых точки: z₁=0, z₂=2i. 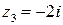Пределы f(z) равны 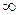во всех трех точках, т.е. все они полюсы. z₁=0 – полюс третьего порядка, т.к. точка является нулем третьей кратности функции 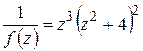, а точки z₂=2i и 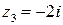– полюса второго порядка, т.к. они двукратные нули функции .

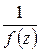Найдем вычеты в этих точках по формуле (2).

●
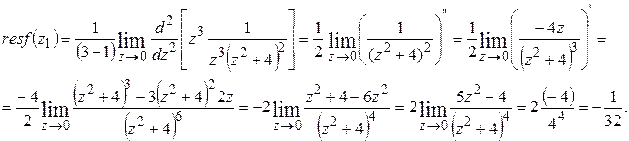
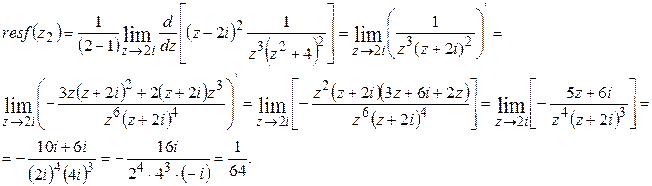
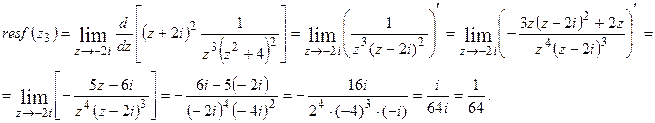
Пример 4.

Вычислить интеграл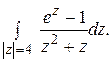

○Чтобы вычислить интеграл по замкнутому контуру нужно воспользоваться таким алгоритмом.

1. Определить контур интегрирования на комплексной плоскости, указав положительное направление обхода контура.

2. Найти особые изолированные точки внутри контура интегрирования, определить их тип и вычислить вычеты в этих точках.

3. Вычислить интеграл по теореме Коши о вычетах.

В рассматриваемом примере контур интегрирования 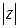=4 – окружность с радиусом 4 и центром в начале координат (рис. 2).

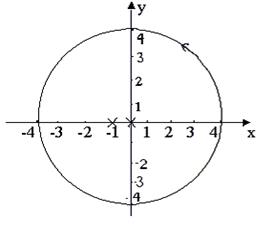
Рис. 2

F(z)имеет две особые изолированные точки (на рис. 2 они обозначены крестами). В примере 2 было установлено, что х₁=0 – устранимая особая точка и resf(0)=0, а 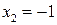– простой полюс с вычетом .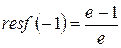