Главная | Обратная связь

Для равноотстоящих узлов интерполяции

Вычисление значений функции для значений аргументов, лежащих в начале таблицы, удобно проводить, пользуясь первой интерполяционной формулой Ньютона. В этом случае интерполяционный многочлен представляют в виде:

F(x) = P_n(x) = a₀ + a₁(x – x₀) + a₂(x –x₀)(x – x₁) +

+ a₃(x –x₀)(x- x₁)(x-x₂) + ... + a_n(x –x₀)(x- x₁)(x-x₂)…(x –x_n-1), (3)

 

при этом неизвестные значения коэффициентов a₀, a₁, a₂, …, a_n вычисляют по формуле

(i = 0, 1, 2, …, n), (4)

то есть

при i = 0 , [0!=1, Δ⁰y₀ = y₀],

при i = 1 = ,

при i = 2 = , и т. д.

 

Обратите внимание, что . (5)

 

После подстановки найденных коэффициентов a_i в выражение (3), получают первую интерполяционную формулу Ньютона:

 

(6)

 

Пример.

Используя первую интерполяционную формулу Ньютона, построить интерполяционный многочлен для функции, заданной таблицей (табл. 1). При составлении таблицы конечных разностей контролировать правильность вычислений.

 

Таблица 1

xi	yi
	8,5
	10,5
	12,0
	13,5
	14,5
	15,5

 

 

Решение.

○Степень многочлена определяется порядком конечных разностей, т.е. для рассматриваемого примера интерполяционный многочлен будет иметь вид

F(x) = P_n(x) = a₀ + a₁(x – x₀) + a₂(x –x₀)(x – x₁) + a₃(x –x₀)(x- x₁)(x-x₂) +

+ a₄(x –x₀)(x- x₁)(x-x₂)(x –x₃) + a₅(x –x₀)(x- x₁)(x-x₂)(x –x₃) (x-x₄) (7)

или

(8)

Вычисление конечных разностей, значений коэффициентов интерполяционного многочлена (особенно высокого порядка), а также значений функции для заданных значений аргументов удобно выполнять в электронной таблице (рис. 1), так как «вручную» выполнять подобные вычисления долго и утомительно.

 

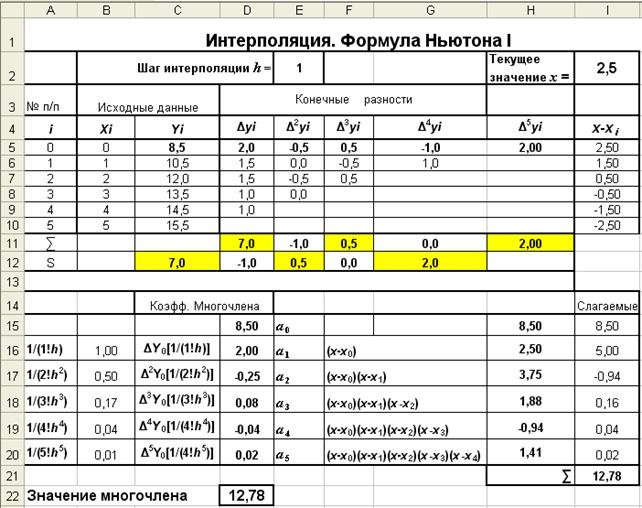
Режим вычислений

 

Рис. 1

В верхнюю часть таблицы следует ввести исходные данные: значение шага интерполяции h, который по условию равен 1, значения аргумента x и соответствующие им значения функции f(x), а также значение аргумента x=2,5, для которого требуется вычислить значение заданной функции, с помощью построенного интерполяционного многочлена.

Реализация вычисления конечных разностей выполняется, как показано в таблице. Значения конечных разностей и значение f(x₀), которые будут использованы в вычислениях по формуле (2), выделены в таблице полужирным начертанием. Правильность полученных конечных разностей подтверждают результаты вычислений, выполненные по формуле (2) (в ячейках D11 и С12, Е11 и D12 и т.д.).

Вычисление коэффициентов интерполяционной формулы (7) целесообразно выполнять, используя свойство (5)

,

а именно:

i = 0

i = 1

i = 2 (9)

i = 3

I = 4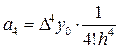

i = 5 = .

 

Для этого в блоке ячеек В16:В20 реализовано вычисление промежуточных значений коэффициентов таким образом, чтобы каждый последующий элемент столбца получался из предыдущего, умножением на 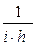. Это позволит при необходимости легко настраивать полученную таблицу на решение задач любой размерности.

В блоке ячеек D16:D20 вычисляются значения коэффициентов интерполяционного многочлена a₀, a₁, …, a₅ (8), путем умножения значений f(x₀), и конечных разностей, полученных в блоке С5: H5 на соответствующие им значения промежуточных коэффициентов (В16:В20).

В соответствии с (7), каждый коэффициент a₁, a₂, a₃, a₄, a₅ соответственно требуется умножить на (x –x₀), (x –x₀)(x- x₁), (x –x₀)(x- x₁)(x-x₂), (x –x₀)(x- x₁)(x-x₂)(x –x₃) (x-x₄). Поэтому в блоке ячеек I5: I10 предусмотрено вычисление значений (x-x_i), которые затем используются для вычисления их произведений в блоке Н16:Н20, причем каждый последующий элемент получается из предыдущего.

В блоке ячеек I15: I20 выполняется вычисление значений каждого члена интерполяционного многочлена, просуммировав которые получается значение интерполяционного многочлена для x=2,5.

Таким образом, получено выражение интерполяционного многочлена:

 

F(x) = P₅(x) = 8,5 + 2(x-0) - 0,25(x-0)(x-1) + 0,08(x-0)(x-1)(x-2) –

-0,04(x-0)(x-1)(x-2)(x-3) + 0,02(x-0)(x-1)(x-2)(x-3)(x-4). (10)

 

Коэффициенты многочлена, полученные при ручном счете по формуле (9), совпадают со значениям коэффициентов, полученными в Excel (см. столбец D15:D20).

Значение F(2,5) = 12,78 (получено в ячейке I21). Подставив значение x = 2,5в (10), получим:

F(2,5) = P₅(2,5) = 8,5 + 2(2,5-0) - 0,25(2,5-0)(2,5-1) + 0,08(2,5-0)(2,5-1)(2,5-2) –

-0,04(2,5-0)(2,5-1)(2,5-2)(2,5-3)+0,02(2,5-0)(2,5-1)(2,5-2)(2,5-3)(2,5-4) = 12,78.

Значение F(x) при x =2,5 при ручном счете и вычислениями в Excel совпадают.

На рис. 2 показана таблица, представленная в режиме формул, в которой алгоритм описанных вычислений становится более наглядным.

Режим формул

Рис. 2.

При использовании электронных таблиц не представляет сложности вычисление значений многочлена для других значений х. Для этого достаточно в ячейке I2 изменить значение х, и мгновенно получим новое значение многочлена. Так же быстро можно изменить исходные значения аргумента х и соответствующие им значения функции y. Для этого в блоки ячеек В5:В10 и С5:С10 – следует ввести новые значения.

Заполнять таблицу тоже достаточно просто, если разумно использовать абсолютную и относительную адресацию ячеек, на которые делаются ссылки в формулах, т.е. применять автозаполнение столбцов и строк. Настроить таблицу на построение многочленов более высоких порядков тоже не сложно, вставив в нужном месте нужное количество строк и столбцов и заполнить нужные ячейки автозаполнением.●