 |
|
Порядок выполнения работы
Задание
1. Выполнить решение примера индивидуального контрольного задания по шести первым точкам (с.77), используя первую интерполяционную формулу Ньютона.
1.4. Реализовать вычисление коэффициентов интерполяционного многочлена средствами MS Excel.
Лабораторная работа 2
Приближенное решение уравнений.
Отделение корней. Уточнение корней методом касательных.
Цель работы
Ознакомление с численными методами решения конечных уравнений.
Основные теоретические положения
Пусть дано уравнение f(x) = 0, где f(x) – непрерывная функция на некотором отрезке. Корни этого уравнения x*– те значения аргумента x, которые обращают уравнение в тождество. Найти приближенное значение корня x* с точностью ε означает указать интервал длиной не более ε, содержащий значение корня x.
При отыскании приближенных значений корней уравнения приходится решать две задачи:
1) отделение корней, т.е. выделение интервалов из области непрерывности функции, в каждом из которых заключен только один корень уравнения;
2) уточнение корня, т.е. построение итерационного процесса, позволяющего сузить границы выделенного интервала до значения заданной точности.
Отделение корней
Графический метод отделения корней
При графическом методе можно построить график функции для уравнения вида f(x) = 0. Значения действительных корней уравнения являются абсциссами точек пересечения функции y = f(x) с осью х.
Пример. Отделить корни уравнения x3 - 8x + 2 = 0 графическим методом, где x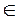 
[-3, 3].
Решение.
○Для отделения корней можно построить график функции y = x3 -8 x + 2 (рис. 1), задав шаг изменения аргумента, например, равным 1. График удобно строить средствами Excel, используя Мастер диаграмм. Значениями действительных корней уравнения являются точки пересечения графика функции с осью x. Из графика видно, что корни находятся на интервалах [-3; -2], [0; 1] и [2; 3]. Если задать шаг изменения аргумента меньше выбранного, можно сузить границы интервалов.■
Рис. 1