 |
|
Закон равномерного распределения энергии по степеням свободы молекул
Закон доказан Л.Больцманом[26] методом классической статистической физики, исходя из предположения, что движение молекул подчиняется законам классической механики:
Для статистической системы, которая находится в состоянии термодинамического равновесия на каждую поступательную и вращательную степени свободы молекулы в среднем приходится одинаковая кинетическая энергия, равная  kT,
kT,
где k = 1,38  10-23
10-23  - постоянная Больцмана.
- постоянная Больцмана.
Если молекула имеет i степеней свободы, то её средняя кинетическая энергия равна: <  > =
> = 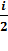 kT.
kT.
Закон Больцмана лежит в основе всей теоpии идеальных газов. Однако, закон оказался неточным, т.к. молекулы – квантовые частицы.
1.10. Закон Максвелла[27] о распределении молекул идеального газа по скоростям
Понятие о функции распределения
Фу́нкция распределе́ния в теории вероятностей — функция, характеризующая распределение случайной величины или случайного вектора; вероятность того, что случайная величина X примет значение, меньшее, чем х, где х — произвольное действительное число.
Функция распределения, основное понятие статистической физики; характеризует плотность вероятности распределения частиц статистической системы по фазовому пространству (т.е. по координатам (qi и импульсам pi) в классической статистической физике или вероятность распределения по квантовомеханическим состояниям в квантовой статистике.
Распределение Ма́ксвелла — распределение вероятности, встречающееся в физике и химии. Оно лежит в основании кинетической теории газов, которая объясняет многие фундаментальные свойства газов, включая давление и диффузию.
Функция распределения молекул идеального газа по скоростям
Закон распределения молекул идеального газа по скоростям, теоретически полученный Максвеллом в 1860 г. определяет, какое число dN молекул однородного (p = const) одноатомного идеального газа из общего числа N его молекул в единице объёма имеет при данной температуре Т скорости, заключенные в интервале от  до
до  + d
+ d  .
.
Идеальный газ – система из большого числа свободных невзаимодействующих частиц, находящихся в непрерывном хаотическом движении, часто сталкивающихся друг с другом. Поэтому в газе при постоянных внешних параметрах устанавливается равновесное состояние, которому соответствует определённое распределение частиц в пространстве по направлениям движения и скоростям. При равновесии средние скорости и число частиц, движущихся в разных направлениях, оказывается одинаковым, о чём свидетельствует отсутствие направленного потока газа при равновесии.
Абсолютная величина скорости молекул, а также проекции скорости на любую ось могут принимать непрерывные значения от нуля до бесконечности. Значит, должна существовать непрерывная функция распределения скоростей f( 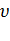 ), показывающая относительное количество молекул, движущихся в единичном интервале скоростей со скоростью, близкой к скорости
), показывающая относительное количество молекул, движущихся в единичном интервале скоростей со скоростью, близкой к скорости 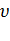 .
.
На языке теории вероятности d  есть плотность вероятности того, что молекула имеет скорость, лежащую в интервале от
есть плотность вероятности того, что молекула имеет скорость, лежащую в интервале от 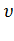 до
до 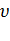 + d
+ d 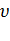 . Тогда сама вероятность описывается выражением: dW = f(
. Тогда сама вероятность описывается выражением: dW = f( 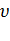 ) •d
) •d 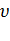 .
.
Нахождение функции распределения f( 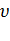 ) молекул по скоростям является главной задачей молекулярно-кинетической теории. Это объясняется тем, что согласно теории вероятности любой функции F(
) молекул по скоростям является главной задачей молекулярно-кинетической теории. Это объясняется тем, что согласно теории вероятности любой функции F( 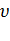 ) (это может быть внутренняя энергия, длина свободного пробега или любая другая функция состояния газа) определяется следующим интегралом:
) (это может быть внутренняя энергия, длина свободного пробега или любая другая функция состояния газа) определяется следующим интегралом:
< F( 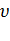 )> =
)> = 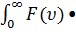 f(
f( 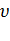 ) •d
) •d 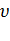 .
.
Впервые найти функцию распределения по скоростям удалось Д.Максвеллу, который исходил из следующих предположений:
1) Идеальный газ состоит из большого числа N одинаковых молекул;
2) Температура газа постоянна (T= const);
3) Молекулы газа совершают тепловое хаотическое движение;
4) На газ не действуют силовые поля.
Функция распределения молекул по скоростям f  )=
)=  определяет относительное число молекул
определяет относительное число молекул  , скорости которых лежат в интервале от
, скорости которых лежат в интервале от 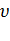 до
до  + d
+ d  .
.
Используя методы теории вероятностей, Максвелл нашел функцию f (  ) -–закон распределения молекул идеального газа по скоростям:
) -–закон распределения молекул идеального газа по скоростям:
f(  ) = 4
) = 4  (
(  )3/2
)3/2  2 еxp {
2 еxp {  },
},
где f(  ) зависит от рода газа (mi – масса молекулы) и от параметров состояния (температуры Т).
) зависит от рода газа (mi – масса молекулы) и от параметров состояния (температуры Т).