 |
|
Нулевое начало термодинамики
Нулевое начало термодинамики названо так потому, что оно было сформулировано уже после того, как первое и второе начало вошли в число устоявшихся научных понятий. Оно утверждает, что изолированная термодинамическая система с течением времени самопроизвольно переходит в состояние термодинамического равновесия и остаётся в нём сколь угодно долго, если внешние условия сохраняются неизменными. Оно также называется общим началом. Термодинамическое равновесие предполагает наличие в системе механического, теплового и химического равновесия, а также равновесия фаз. Классическая термодинамика постулирует лишь существование состояния термодинамического равновесия, но ничего не говорит о времени его достижения.
Первый закон термодинамики
Теплота, сообщаемая системе, расходуется на увеличение её внутренней энергии и на совершение работы ею против внешних сил (рис. 121).
Первый закон термодинамики для элементарного процесса:
 = dU +
= dU + 
или для конечного процесса: Q=  + A.
+ A.

Рис. 121.
Обмен энергией между термодинамической системой и окружающими телами в результате теплообмена и совершаемой работы.
Если система периодически возвращается в первоначальное состояние, то 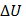 = 0. Тогда согласно первому закону термодинамики: А =
= 0. Тогда согласно первому закону термодинамики: А =  , т.е. вечный двигатель первого рода[38] невозможен (рис. 122).
, т.е. вечный двигатель первого рода[38] невозможен (рис. 122).



Рис. 122. Предлагаемые «изобретателями» в истории техники «вечные двигатели»
Энтальпия системы
Работа изменения объёма газа в изобарном процессе (m – const;P = const): A = P•dV = d (PV). (1)
С учётом формулы (1) первый закон термодинамики примет вид:
 = dU +
= dU +  = dU + d (PV) = d (U + PV). (2)
= dU + d (PV) = d (U + PV). (2)
Введём новую величину, называемую энтальпией:
I = U + PV, (Дж) (3)
Энтальпия I является функцией состояния, т.к. величины U,P.V сами являются функциями состояния.
С учётом формулы (3) при P = const первый закон термодинамики примет вид:
 = ∆I = I2 – I1.
= ∆I = I2 – I1.
Энтальпия – функция состояния, приращение которой в изобарном процессе даёт тепло, полученное системой.
Полная энергия. Закон сохранения полной энергии
Полной энергией системы называется сумма её механической и внутренней энергий:W = Eм + U.
Замкнутой (изолированной) называется термодинамическая система, которая не обменивается энергией ни в какой форме с внешней средой.
Для такой системы справедливо: 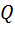 =0;А = 0, тогда из первого закона термодинамики следует: dU = 0 => U= const.
=0;А = 0, тогда из первого закона термодинамики следует: dU = 0 => U= const.
Если в замкнутой системе Eм = const и U = const, то W =const.
Полная энергия изолированной системы остаётся неизменной при любых процессах, в ней происходящих.
Понятие изолированной системы – идеализация, все реальные системы незамкнуты.
Теплоёмкость
Для характеристики тепловых свойств тел в термодинамике используют понятие теплоёмкости.
Теплоёмкостью тела называется отношение бесконечно малого количества теплоты, полученного телом в рассматриваемом термодинамическом процессе, к соответствующему приращению его температуры: C =  ,
,  ),
),
Значение теплоёмкости С зависит от массы тела, его химического состава, термодинамического состояния и процесса, в котором сообщается теплота  .
.
Удельной теплоёмкостью с называется теплоёмкость единицы массы вещества: с =  =
=  , (
, (  ).
).
Удельная теплоёмкость не зависит от массы вещества.
Молярной (мольной) теплоёмкостью называется теплоёмкость одного моля вещества:  =
=  =
=  =
=  c, (
c, (  ).
).
Теплоёмкость в изохорном и изобарном процессах идеального газа
Для газов различают теплоёмкости при постоянном объёме (в изохорном процессе) CV и при постоянном давлении (в изобарном процессе) CP.
1). Молярная теплоёмкость идеального газа при постоянном объёме 
Первый закон термодинамики:
 dU +
dU + 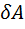 =dU+P•dV. (1)
=dU+P•dV. (1)
Молярная теплоёмкость газа:  =
=  Для одного моля газа (
Для одного моля газа (  1моль):
1моль):  =
=  =>
=>  =
=  dT. (2)
dT. (2)
Из формул (1) и (2) для моля газа следует:
 dT=
dT=  + PdV. (3)
+ PdV. (3)
В случае идеального газа при V = const работа внешних сил равна нулю ( 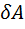 = 0) и сообщаемое газу извне тепло идёт только на увеличение его внутренней энергии:
= 0) и сообщаемое газу извне тепло идёт только на увеличение его внутренней энергии:  =
=  . (4)
. (4)
Для моля идеального газа: d  =
=  R•dT. (5)
R•dT. (5)
Тогда из формул (4) и (5) следует:  =
=  R.
R.
2). Молярная теплоёмкость идеального газа при постоянном давлении  Уравнение Майера
Уравнение Майера
Если газ нагревается при постоянном давлении (P = const), то уравнение первого закона термодинамики можно представить в виде:
 •dT = d
•dT = d  + P•dV
+ P•dV
или  =
=  +
+  , где
, где  =
=  .
.
В итоге получим:  =
=  +
+  . (6)
. (6)
Уравнение Клапейрона – Менделеева для моля идеального газа (  = 1моль): P
= 1моль): P  = RT|
= RT|  => P
=> P 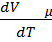 = R
= R  = R – универсальная газовая постоянная.
= R – универсальная газовая постоянная.
С учётом последнего уравнения уравнение (6) можно представить в виде:  =
=  + R. Последнее уравнение называется уравнением Майера.
+ R. Последнее уравнение называется уравнением Майера.
В окончательном виде уравнение Майера:
 -–
-–  = R;
= R;
CP – CV =  R;
R;
сP – cv =  .
.
Как видно из уравнения Майера всегда СР > CV, т.к. при нагревании газа при постоянном давлении требуется ещё дополнительное количество теплоты на совершение работы расширения газа, т.к. постоянство давления обеспечивается увеличением объёма газа.
Из предудущих уравнений и уравнения Майера следует:
 =
=  R + R =
R + R =  R,
R,
т.е. 
 R.
R.
При рассмотрении термодинамических процессов важно знать характерное для каждого газа соотношения:  =
=  ,
,
называемое коэффициентом Пуассона или показателем адиабаты.
Для различных газов этот показатель имеет следующие значения:
- для одноатомного газа (i = 3):  = 1,67;
= 1,67;
- для двухатомного газа (i = 5):  = 1,40;
= 1,40;
- для трёхатомного и многоатомного газа (i = 6):  = 1,33.
= 1,33.
Закон равномерного распределения энергии идеального газа по степеням свободы молекул приводит к выводу, что теплоёмкости газов зависят от числа степеней свободы молекул и не зависят от температуры. Экспериментальные данные опровергают этот вывод классической теории теплоёмкости: с увеличением температуры теплоёмкость газов возрастает, а с понижением температуры – убывает. Объяснение этого дано в квантовой теории теплоёмкостей.
Теплоёмкость твёрдых тел. Правило Дюлонга и Пти
Для твёрдых тел не различают теплоёмкости CV и CP. Основной вклад в теплоёмкости неметаллических твёрдых тел вносит энергия тепловых колебаний частиц, находящихся в узлах кристаллических решёток. Для неметаллов незначительный вклад в теплоёмкость вносит вырожденный электронный газ[39].
В основе классической теории теплоёмкости твёрдых тел лежит закон равномерного распределения энергии по степеням свободы. Однородное твёрдое тело рассматривается как система независимых друг от друга частиц, имеющих 3 степени свободы и совершающих колебания с одинаковой частотой. Средняя энергия, приходящаяся на одну степень свободы < W > = kT. Внутренняя энергия моля твёрдого тела:
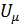 = 3 Na
= 3 Na 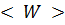 =
=  3 NakT = 3RT,
3 NakT = 3RT,
где Na – постоянная Авогадро, k – постоянная Больцмана, R = kNa – универсальная газовая постоянная.
Молярная теплоёмкость твёрдого тела с атомной кристаллической решёткой:
 =
=  3 R = 25
3 R = 25  5,97
5,97  .
.
Правило Дюлонга и Пти: Молярная теплоёмкость всех химически простых кристаллических твёрдых тел приблизительно равна 6  .
.
Согласно этому правилу молярная теплоёмкость твёрдых тел не должна зависеть от температуры, ни от каких-либо характеристик кристаллов. Опыты опровергают это и указывают на зависимость теплоёмкости от температуры, в особенности в области низких температур. Причины расхождения с опытом классической теории теплоёмкости твёрдых тел состоят в ограниченности использования закона равномерного распределения энергии по степеням свободы и непригодности его в области низких температур, где среднюю энергию колеблющихся частиц в кристаллической решетке необходимо вычислять по законам квантовой механики.
Применение первого закона термодинамики к изопроцессам идеального газа
С учётом того, что  =
=  dT и
dT и  = PdV , первый закон термодинамики можно представить в виде:
= PdV , первый закон термодинамики можно представить в виде:  dT =dU + PdV.
dT =dU + PdV.
Изобарный процесс (m = const, P = const)
Первый закон термодинамики для изобарного процесса имеет вид:
 dU+
dU+ 
где  =
= 
 dT; dU =
dT; dU = 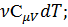
 = PdV =
= PdV =  .
.
Из последнего равенства следует: R =  , т.е. R =
, т.е. R =  при
при  = 1 моль; dT = 1K, т.е. универсальная газовая поcтоянная R численно равна работе, совершаемой одним молем идеального газа при нагревании его на один градус.
= 1 моль; dT = 1K, т.е. универсальная газовая поcтоянная R численно равна работе, совершаемой одним молем идеального газа при нагревании его на один градус.
Согласно закону Гей-Люссака, при изобарном процессе в идеальном газе:
 const.
const.
График изобарического расширения газа от объёма VA до VB. AB здесь является изобарой, изображён на рис. 123.

Рис. 123.
Изохорный процесс (m = const; V = const)
Так как в изохорном процессе V= const =>  = PdV = 0, т.е. в изохорном процессе работа не совершается.
= PdV = 0, т.е. в изохорном процессе работа не совершается.
Первый закон термодинамики для изохорного процесса :  = dU,
= dU,
т.е. всё количество теплоты, подводимое к газу идёт на изменение его внутренней энергии, где  = dU =
= dU =  .
.
Математически изохорный процесс описывается уравнением Шарля:  = const.
= const.
График изохорного процесса – изохора (рис. 124).
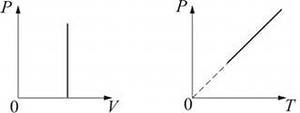
Рис. 124.
Изотермический процесс (m = const, T = const)
Так как при изотермическом процессе T= const, то изменение внутренней энергии dU = 0, т.е. внутренняя энергия системы U = const.
Первый закон термодинамики для изотермического процесс:  =
=  ,
,
т.е. всё количество теплоты, сообщаемое газу, расходуется на совершение работы против внешних сил.
Для конечного процесса: A =  .
.
Т.к. согласно уравнению Менделеева – Клапейрона: РV =  RT => P =
RT => P = 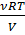 . Таким образом, A =
. Таким образом, A =  = ln
= ln  =
=  =
=  ln
ln  .
.
Т.е.  = A = ln
= A = ln  =
=  =
=  ln
ln  .
.
Чтобы при работе расширения температура не уменьшалась, к газу в течении изотермического процесса необходимо подводить количество теплоты, эквивалентное работе расширения.
Уравнением изотермического процесса является уравнение Бойля- Мариотта:
РV = const.
Графиком изотермического процесса является гипербола – изотерма (рис. 125):
T2> T1

Рис. 125.
Применение первого закона термодинамики к адиабатному процессу (  = 0)
= 0)
Так как в адиабатном процессе отсутствует теплообмен с внешней средой  = 0), то первый закон термодинамики для адиабатного процесса имеет вид:
= 0), то первый закон термодинамики для адиабатного процесса имеет вид:
 ,
,
т.е. при адиабатном процессе работа совершается за счёт убыли внутренней энергии системы, где - dU – убыль внутренней энергии системы.
Тогда: dU =  и, соответственно:
и, соответственно:  =
=  . (1)
. (1)
При адиабатическом расширении газ охлаждается (  = PdV > 0, а dT < 0); при адиабатическом сжатии газ нагревается (
= PdV > 0, а dT < 0); при адиабатическом сжатии газ нагревается (  = PdV < 0, а dT > 0).
= PdV < 0, а dT > 0).
Найдём связь между параметрами состояния идеального газа (P; V) в адиабатном процессе.
Представим (1) в виде:  = PdV =
= PdV = 
Из уравнения Клапейрона – Менделеева следует:
PdV =  = d(PV) = P•dV + V•dP.
= d(PV) = P•dV + V•dP.
Таким образом, PdV = 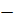
 (P•dV + V•dP).
(P•dV + V•dP).
Так как, согласно уравнению Майера:  то
то  |:
|: 
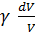 +
+  = 0, где
= 0, где  .
.
Так как  =
=  d(lnV) = d(ln
d(lnV) = d(ln  и
и  = d(lnP), то уравнение можно представить в виде:
= d(lnP), то уравнение можно представить в виде:
d(ln  и d(ln
и d(ln 
Таким образом, в равновесном адиабатном процессе изменение состояния идеального гага описывается уравнением Пуассона (уравнением адиабаты):
P  = сonst.
= сonst.
Последнее уравнение можно записать также в виде:
P  или V
или V  .
.
На диаграмме в координатах (P;V) адиабата имеет вид гиперболы (рис. 126):

Рис. 126.
Адиабата идёт круче изотермы. При адиабатном сжатии увеличение давления обусловлено не только уменьшением объёма газа, как при изотермическом сжатии, но и увеличением температуры. При адиабатном расширении температура газа уменьшается, поэтому давление падает быстрее, чем при изотермическом расширении.
Работа A12 =  =
=  (T1
(T1  T2).
T2).
Из уравнения Майера и соотношения  , следует:
, следует:  =
=  .
.
Поэтому A12 =  (T1
(T1  T2) =
T2) =  [1
[1 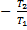 ].
].
Из уравнения адиабаты следует:  =
=  =
= 
Тогда: A12 =  [1
[1  или A12 =
или A12 =  [1
[1 
Графически работа численно равна площади криволинейной трапеции V2V4P2′P0.
Работа адиабатного расширения 1  меньше, чем при изотермическом процессе. При адиабатном расширении происходит охлаждение газа, тогда как при изотермическом расширении температура поддерживается за счёт притока извне эквивалентного количества теплоты.
меньше, чем при изотермическом процессе. При адиабатном расширении происходит охлаждение газа, тогда как при изотермическом расширении температура поддерживается за счёт притока извне эквивалентного количества теплоты.