Главная | Обратная связь

Второе начало термодинамики

Исторически второе начало термодинамики возникло из анализа работы тепловых машин (С. Карно, 1824). Существует несколько его эквивалентных формулировок. Само название «второе начало термодинамики» и исторически первая его формулировка (1850) принадлежат Р. Клаузиусу.

Первое начало термодинамики, выражая закон сохранения и превращения энергии, не позволяет установить направление протекания термодинамических процессов. Кроме того, можно представить множество процессов, не противоречащих первому началу, в которых энергия сохраняется, а в природе они не осуществляются.

Опыт показывает, что разные виды энергии неравноценны в отношении способности превращаться в другие виды энергии. Механическую энергию можно целиком превратить во внутреннюю энергию любого тела. Для обратных превращений внутренней энергии в другие виды существуют определённые ограничения: запас внутренней энергии ни при каких условиях не может превратиться целиком в другие виды энергии. С отмеченными особенностями энергетических превращений связано направление протекания процессов в природе.

Второе начало термодинамики - принцип, устанавливающий необратимость макроскопических процессов, протекающих с конечной скоростью.

В отличие от чисто механических (без трения) или электродинамических (без выделения джоулевой теплоты) обратимых процессов, процессы, связанные с теплообменом при конечной разности температур (т. е. текущие с конечной скоростью), с трением, диффузией газов, расширением газов в пустоту, выделением джоулевой теплоты и т.д., необратимы, т. е. могут самопроизвольно протекать только в одном направлении.

Второе начало термодинамики отражает направленность естественных процессов и налагает ограничения на возможные направления энергетических превращений в макроскопических системах, указывая, какие процессы в природе возможны, а какие – нет.

Второе начало термодинамики является постулатом, не доказываемым в рамках термодинамики. Оно было создано на основе обобщения опытных фактов и получило многочисленные экспериментальные подтверждения.

Формулировки второго закона термодинамики

1). Формулировка Карно: наибольший КПД тепловой машины не зависит от рода рабочего тела и вполне определяется предельными температурами, между которыми машина работает.

2). Формулировка Клаузиуса: невозможен процесс единственным результатом которого является передача энергии в форме теплоты от тела менее нагретого, к телу более нагретому.

Второе начало термодинамики не запрещает переход теплоты от менее нагретого тела к более нагретому. Такой переход осуществляется в холодильной машине, но при этом внешние силы осуществляют работу над системой, т.е. этот переход не является единственным результатом процесса.

3). Формулировка Кельвина: невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, в эквивалентную ей работу.

На первый взгляд может показаться, что такой формулировке противоречит изотермического расширения идеального газа. Действительно, всё полученное идеальным газом от какого-то тела тепло превращается полностью в работу. Однако получение тепла и превращение его в работу не единственный конечный результат процесса; кроме того, в результате процесса происходит изменение объёма газа.

P.S.: необходимо обратить внимание на слова «единственным результатом»; запреты второго начала снимаются, если процессы, о которых идёт речь, не являются единственными.

4). Формулировка Оствальда[41]: осуществление вечного двигателя второго рода невозможно.

Вечным двигателем второго рода называется периодически действующее устройство, которое совершает работу за счёт охлаждения одного источника теплоты.

Примером такого двигателя мог бы служить судовой двигатель, получающий тепло из моря и использующий его для движения судна. Такой двигатель был бы практически вечным, т.к. запас энергии в окружающей среде практически безграничен.

С точки зрения статистической физики второе начало термодинамики имеет статистический характер: оно справедливо для наиболее вероятного поведения системы. Существование флуктуаций препятствует точному его выполнению, однако вероятность сколь-нибудь значительного нарушения крайне мала.

Энтропия

Понятие «энтропия» введено в науку Р.Клаузиусом в 1862 г. и образовано из двух слов: «эн» - энергия, «тропэ» - превращаю.

Согласно нулевому началу термодинамики изолированная термодинамическая система с течением времени самопроизвольно переходит в состояние термодинамического равновесия и остаётся в нём сколь угодно долго, если внешние условия сохраняются неизменными.

В равновесном состоянии все виды энергии системы переходят в тепловую энергию хаотического движения атомов и молекул, составляющих систему. Никакие макроскопические процессы в такой системе невозможны.

Количественной мерой перехода изолированной системы в равновесное состояние служит энтропия. По мере перехода системы в равновесное состояние её энтропия возрастает и достигает максимума при достижении равновесного состояния.

Энтропия является функцией состояния термодинамической системы, обозначается: [S] = .

Теоретическое обоснование: приведённая теплота, энтропия

Из выражения для КПД цикла Карно: = = = следует, что = или = 0, где – количество теплоты, отдаваемое рабочим телом холодильнику, принимаем: < 0.

Тогда последнее соотношение можно записать в виде:

+ = 0 (1)

Отношение теплоты, полученной телом в изотермическом процессе, к температуре теплоотдающего тела называется приведённым количеством теплоты: = . (2)

С учётом формулы (2) формулу (1) представим в виде:

+ = 0, (3)

т.е. для цикла Карно алгебраическая сумма приведённых количеств теплоты равна нулю.

Приведённое количество теплоты, сообщаемое телу на бесконечно малом участке процесса: .

Приведённое количество теплоты для произвольного участка:

= .

Строгий теоретический анализ показывает, что для любого обратимого кругового процесса сумма приведённых количеств теплоты равна нулю:

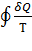= 0. (4)

Из равенства нулю интеграла (4) следует, что подинтегральная функция есть полный дифференциал[42] некоторой функции, которая определяется только состоянием системы и не зависит от пути, каким система пришла в это состояние:

= dS. (5)

Однозначная функция состояния, полным дифференциалом которой является , называется энтропией S, ( ).

Формула (5) справедлива лишь для обратимых процессов, в случае неравновесных необратимых процессов такое представление dS несправедливо.

Свойства энтропии

1). Энтропия определяется с точностью до произвольной постоянной. Физический смысл имеет не сама энтропия, а разность энтропий двух состояний:

∆S = S₂ S₁ = . (6)

Пример: если система (идеальный газ) совершает равновесный переход из состояния 1 в состояние 2, то изменение энтропии равно:

∆S₁₂ = S₂ S₁ = = ,

где dU = ; = P dV = RT .

Тогда: ∆S₁₂ = = + R = ( + R ln ),

т.е. изменение энтропии ∆S₁₂ идеального газа при переходе его из состояния 1 в состояние 2 не зависит от вида процесса перехода.

В общем случае в формуле (6) приращение энтропии ∆S не зависит от пути интегрирования.

2). Абсолютное значение энтропии можно установить с помощью третьего начала термодинамики (теоремы Нернста[43]):

Энтропия любого тела стремиться к нулю при стремлении к абсолютному нулю его температуры: 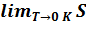= 0.

Таким образом, за начальную точку отсчёта энтропии принимают S₀ = 0 при T = 0 K.

3). Энтропия величина аддитивная, т.е. энтропия системы из нескольких тел является суммой энтропий каждого тела: S = .

4). Как и внутренняя энергия, энтропия есть функция параметров термодинамической системы P, V, T.

5), Процесс, протекающий при постоянной энтропии (S=const) называется изоэнтропийным.

В равновесных процессах без передачи тепла ( 0) энтропия не меняется.

В частности, изоэнтропийным является обратимый адиабатный процесс: для него 0; ∆S = 0, т.е. S = const.

6). При постоянном объёме (V = const) энтропия является монотонно возрастающей функцией внутренней энергии тела.

Действительно, из первого закона термодинамики следует, что при dV = 0 имеем: = dU, тогда dS = . Но температура T > 0 всегда. Поэтому приращения dS и dU имеют один и тот же знак, что и требовалось доказать.

Примеры изменения энтропии в различных процессах

1). При изобарном расширении идеального газа

∆S = C_P ln .

2). При изохорном расширении идеального газа

∆S = C_V ln .

3). При изотермическом расширении идеального газа

∆S = R ln = R ln .

4). При фазовых переходах

Пример: найти изменение энтропии при превращении массы m_л льда при температуре Т₁ в пар (Т_п = 373 К).

Решение

Первый закон термодинамики: dU + = + P dV.

Из уравнения Менделеева – Клапейрона следует: P = => + dV.

При переходе из одного агрегатного состояния в другое, общее изменение энтропии складывается из изменений в отдельных процессах:

а). Нагревание льда от температуры Т₁ до температуры плавления Т₀ = 273 К:

∆S₁ = dT = mc_л ln ,

где c_л – удельная теплоёмкость льда.

Б). Плавление льда: ∆S₂ = = , где – удельная теплота плавления льда.

В). Нагревание воды от температуры Т₀ до температуры кипения Т_к = 273 К:

∆S₃ = dT = mc_в ln , где с_в – удельная теплоёмкость воды.

Г). Испарение воды: ∆S₄ = = , где r – удельная теплота парообразования воды.

Тогда общее изменение энтропии:

∆S = ∆S₁ + ∆S₂ + ∆S₃ + ∆S₄ = mc_л ln + + mc_в ln + .

Принцип возрастания энтропии

Энтропия замкнутой системы при любых, происходящих в ней процессах не убывает:

dS 0,

или для конечного процесса: ∆S 0 => S₂ S_1.

Знак равенства относится к обратимому процессу, знак неравенства – к необратимому. Последние две формулы – математическое выражение второго закона термодинамики. Таким образом, введение понятия «энтропия» позволило строго математически сформулировать второе начало термодинамики.

Необратимые процессы приводят к установлению равновесного состояния. В этом состоянии энтропия изолированной системы достигает максимума. Никакие макроскопические процессы в такой системе невозможны.

Величина изменения энтропии является качественной характеристикой степени необратимости процесса.

Принцип возрастания энтропии относится к изолированным системам. Если система неизолированная, то её энтропия может и убывать.

Вывод: т.к. все реальные процессы необратимые, то все процессы в замкнутой системе ведут к увеличению её энтропии.

Теоретическое обоснование принципа

Рассмотрим замкнутую систему, состоящую из нагревателя, холодильника, рабочего тела и «потребителя» совершаемой работы (тело, обменивающееся с рабочим телом энергией только в форме работы), совершающую цикл Карно. Это обратимый процесс, изменение энтропии которого равно:

∆S = ∆S_р + ∆Sн + ∆S_х + ∆S_п,

где ∆S_р – изменение энтропии рабочего тела; ∆S_н – изменение энтропии нагревателя; ∆S_х – изменение энтропии холодильника; ∆S_п – изменение энтропии «потребителя» работы.

Так как рабочее тело при совершении цикла Карно возвращается в исходное положение, то ∆S_р = 0. Так как «потребитель» работы получает энергию в форме работы, то ∆S_п = 0.

Изменение энтропии нагревателя и холодильника в изотермических процессах:

∆S_н = ; ∆S_х = ,

где и – количество теплоты, полученной рабочим телом за один цикл соответственно от нагревателя ( и холодильника ( .

С учётом выше изложенного изменение энтропии системы равно:

∆S = ( + ).

Так как цикл Карно обратимый, то КПД цикла равен: = =

или = .

В результате получаем, что энтропия замкнутой системы, совершающей обратимый цикл, не изменяется: ∆S_обр. = 0, т.е. S = const.

Все реальные процессы необратимы. Рассмотрим необратимый цикл. КПД необратимого цикла всегда меньше КПД цикла Карно:

< ( и + < 0 | => + < 0,

т.е. энтропия замкнутой системы, совершающей необратимый цикл, возрастает:

∆S_необр. > 0.

Эти выводы можно обобщить для произвольных процессов в замкнутой системе в виде принципа возрастания энтропии.

Основное соотношение термодинамики. Свободная энергия

Первый закон термодинамики: = dU + (1)

Изменение энтропии обратимого процесса: dS = .(2)

Второй закон термодинамики: dS 0. (3)

Из формул (2) и (3) следует: 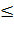T dS, (4)

где Т – температура тела, сообщающего системе энергию в процессебесконечно малого изменения состояния системы.

Объединив первый и второй законы термодинамики, получим основное соотношение термодинамики: T dS dU + (5)

Основное соотношение термодинамики для обратимого процесса:

T dS = dU + (6)

или = (dU T dS) = d (U TS) S dT = dF S dT,

где F = U TS – свободная энергия (энергия Гельмгольца[44]). (7)

Свободная энергия F является разностью двух функций состояний и поэтому то же является функцией состояния термодинамической системы.

Рассмотрим обратимый изотермический процесс, когда dT = 0 и = dF.

При переходе системы из состояния 1 в состояние 2 в обратимом изотермическом процессе: А_изот. = F₁ F₂.

Таким образом, убыль свободной энергии является мерой работы, которую система совершает в обратимом изотермическом процессе.

Из формулы (7) следует: U = F + TS, где TS – связанная энергия. (8)