Главная | Обратная связь

Теоретичні відомості

Сферичний резонатор – це є об’єм, обмежений сферичною провідною поверхнею. Розглянемо ідеальну провідну сферу з радіусом а заповнену діелектриком без втрат з проникністю ε (рис. 8.1). Щоб визначити власні параметри такого резонатора потрібно розв’язати рівняння Гельмгольца у сферичних координатах r, φ, θ.

У сферичному резонаторі, як і в інших об’ємних резонаторах, можуть існувати коливання магнітного H_nmq та електричного E_nmq типів. Індекси m, n, q – позначають кількість варіацій поля уздовж координатних осей r, φ, θ.

Рис. 8.1. Сферичний резонатор

 

Власні коливання у сферичному резонаторі описуються функціями:

 

; (8.1)

і

, (8.2)

де і 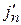– сферична функція Бесселя та її перша похідна з аргументу;

– приєднані функції Лежандра 1-го роду;

– хвильове число;

– циклічна частота;

ε_a, μ_a – абсолютні діелектрична й магнітна проникності об’єму резонатора.

Індекси m повинні бути цілими (m = 0, 1, 2, …) через однозначність полів у кожній точці простору у сфері. Індекси n також повинні бути цілими (n = 1, 2, …) через кінцевий характер полів при θ=0 і θ=π. Оскільки , (m = 1, 2, …), то при n = 0 електромагнітне поле також дорівнює нулю.

При r=a на ідеально провідній поверхні сфери повинні задовольнятися граничні умови, при яких дорівнюють нулю тангенційні компоненти поля. Тому власні частоти магнітних хвиль визначаються з рівняння

 

, n = 1, 2, …, (8.3)

 

а власні частоти електричних коливань – з рівняння

 

, n=1, 2, … . (8.4)

 

Якщо n – ціле число, то q-й додатний корінь рівняння (8.3) дає власну частоту коливання H_nmq , а q-й додатний корінь рівняння (8.4) – власну частоту коливання E_nmq у сферичному резонаторі.

Власні частоти сферичного резонатора не залежать від індексу m, а залежать тільки від індексів n і q. Оскільки кожному n відповідає 2n + 1 різних кутових функцій і , то кожна власна частота має кратність виродження 2n + 1. Це пов’язано з високою симетрією сфери. Вибір осі z (θ = 0) для сфери довільний, при іншому виборі отримуємо нові коливання з такою ж частотою.

Таким чином власні частоти коливань сферичного резонатора будуть дорівнюватися коливанням магнітного типу

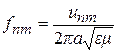(8.5)

і для коливань електричного типу

, (8.6)

де u_nm означає m-й корінь рівняння (8.3) (для коливань магнітного типу);

u'_nm – m-й корінь рівняння (8.4) (для коливань електричного типу).

Нижчим типом коливань сферичного резонатора буде Е₀₁₁ (u’₁₁=2,75). Нижчим магнітним типом коливання буде (u₁₁=4,50). Розподіл електричних і магнітних силових ліній коливань і показано на рис. 8.2.

 

а б

Рис. 8.3. Власні коливання у сферичному резонаторі: а – E₁₀₁ типу, б – H₁₀₁ типу

(вісь z спрямована у вертикальному напрямку)

 

Частоти коливань і є трикратно виродженими. Легко показати, що поля коливань і отримуються повертанням полів і на кут π/2 у площині x0z або y0z і мають такі ж самі власні частоти (поляризаційне виродження).

Власна добротність об’ємного резонатора може бути визначена через відношенню накопиченої резонатором енергії до енергії, що витрачається за період коливань, або

, (8.7)

 

де W – накопичена в резонаторі енергія;

– потужність втрат;

f₀ – частота резонансних коливань.

Енергетична формула (8.7) для розрахунку добротності є наближеною, тому що не враховує вироджений характер власних коливань сферичного резонатора. Вплив кінцевої провідності стінок резонатора може призвести до радикальної перебудови системи коливань резонатора. Однак, на практиці наявність елементів зв’язку в значної мірі порушує ідеальну симетрію резонатора і в значної мірі знімає виродження його власних коливань.

Завдяки оптимальному співвідношенню об’єму і площини поверхні сферичний резонатор має найбільшу теоретичну власну добротність серед об’ємних резонаторів інших конфігурацій однакового об’єму. Однак, технологічні труднощі виготовлення сферичних резонаторів, складність їх підключення до хвилевідного тракту та виродження власних коливань обумовили незначне розповсюдження сферичних порожистих резонаторів на практиці.