Главная | Обратная связь

Побудова економіко-математичної моделі.

Позначимо через х_ij площу (га) і-ої земельної ділянки, що буде засіяна j-м сортом озимої пшениці (домовимося, що сорти «Миронівська-808», «Безоста-1», «Одеська-51» відповідатимуть номерам 1, 2, 3), (і = 1, 2, 3), (j = 1, 2, 3).

Тоді використання земельних угідь описуватиме така система обмежень:

;

;

.

Використання посівного матеріалу формально можна описати так:

;

;

.

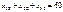Валовий збір зерна розраховується як сума добутків урожайностей відповідних сортів пшениці на їх посівні площі, тобто:

Отже, економіко-математична модель задачі загалом буде мати вигляд:

за умов:

.

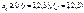2.5(1)

Розглянемо геометричну інтерпретацію задачі лінійного програмування на прикладі. Нехай фермер прийняв рішення вирощувати озиму пшеницю і цукрові буряки на площі 20 га, відвівши під цукрові буряки не менше як 5 га. Техніко-економічні показники вирощування цих культур маємо у табл. 2.3:

Таблиця 2.3

ПОКАЗНИКИ ВИРОЩУВАННЯ СІЛЬСЬКОГОСПОДАРСЬКИХ КУЛЬТУР

Показник (із розрахунку на 1 га)	Озима пшениця	Цукрові буряки	Наявний ресурс
Затрати праці, людино-днів
Затрати праці механізаторів, людино-днів
Урожайність, тонн	3,5		—
Прибуток, тис. грн	0,7		—

Критерієм оптимальності є максимізація прибутку.

Запишемо економіко-математичну модель структури виробництва озимої пшениці та цукрових буряків, ввівши такі позначення:

х₁ — шукана площа посіву озимої пшениці, га;

х₂ — шукана площа посіву цукрових буряків, га.

Задача лінійного програмування має такий вигляд:

max Z = 0,7x₁ + x₂ (2.10)

за умов:

x₁ + x₂ ≤ 20; (2.11)

5 x₁ + 25 x₂ ≤ 270; (2.12)

2 x₁ + 8 x₂ ≤ 80; (2.13)

x₂ ≥ 5; (2.14)

x₁ ≥ 0, x₂ ≥ 0. (2.15)

Геометричну інтерпретацію задачі зображено на рис. 2.2.

Рис. 2.2. Область допустимих розв’язків задачі

Область допустимих розв’язків цієї задачі дістаємо так. Кожне обмеження, наприклад x₁ + x₂ ≤ 20, задає півплощину з граничною прямою x₁ + x₂ = 20. Будуємо її і визначаємо півплощину, яка описується нерівністю x₁ + x₂ ≤ 20. З цією метою в нерівність x₁ + x₂ ≤ 20 підставляємо координати характерної точки, скажімо, x₁ = 0 і x₂ = 0. Переконуємося, що ця точка належить півплощині x₁ + x₂ ≤ 20. Цей факт на рис. 2.2 ілюструємо відповідною напрямленою стрілкою. Аналогічно будуємо півплощини, які відповідають нерівностям (2.11)—(2.15). У результаті перетину цих півплощин утворюється область допустимих розв’язків задачі (на рис. 2.2 — чотирикутник ABCD). Цільова функція Z = 0,7 x₁ + x₂ являє собою сім’ю паралельних прямих, кожна з яких відповідає певному значенню Z. Зокрема, якщо Z = 0, то маємо 0,7 x₁ + x₂ = 0. Ця пряма проходить через початок системи координат. Коли Z = 3,5, то маємо пряму 0,7 x₁ + x₂ = 3,5.

Задача 2.6.

Розв’язати графічним методом задачу лінійного програмування

.

Розв’язання. Маємо n = 7 — кількість змінних, m = 5 — кількість обмежень. Виберемо як вільні змінні х₁ та х₂ і виразимо через них всі інші базисні змінні. З першого рівняння маємо:

(2.19.2)

З третього рівняння:

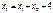, (2.19.3)

а з четвертого:

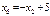. (2.19.4)

Підставляючи (2.19.2) в друге рівняння системи і (2.19.4) в останнє, розв’язуємо їх відносно х₄ та х₇. Отримаємо:

;

.

Далі за алгоритмом беремо х₁ = 0 та х₂ = 0 — координатні осі; інші обмежуючі прямі знаходимо, узявши х₃ = 0, х₄ = 0, х₅ = 0, х₆ = 0, х₇ = 0. Багатокутник допустимих розв’язків зображено на рис. 2.12.

Рис. 2.12

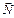Знайдемо вигляд функціонала, вираженого через х₁ та х₂. Для цього знайдені щойно вирази для х₃, х₄, х₅, х₆ та х₇ через вільні змінні х₁ і х₂ підставимо у функціонал і, звівши подібні члени, отримаємо: . Відкидаючи вільний член, маємо: . Будуємо вектор (–5, –2), перпендикулярно до нього — пряму F'. Рухаючи пряму F' в напрямку, протилежному (необхідно знайти мінімальне значення функції F), отримаємо точку мінімуму — А (рис. 2.13).

Рис. 2.13

У точці А перетинаються дві обмежуючі прямі: х₆ = 0 та х₇ = 0. Отже, для відшукання її координат необхідно розв’язати систему рівнянь:

Розв’язком системи є х₁*= 8,5; х₂*= 5. Підставивши ці значення у відповідні вирази, знайдемо оптимальні значення базисних змінних:

Х₃*= 0,5; х₄*= 16,5; х₅*= 17,5; х₆*= 0; х₇*= 0.

Підстановкою значень х₁* та х₂* в лінійну функцію F отримуємо значення цільової функції:

 

Задача 2.7.

Фірма спеціалізується на виробництві офісних меблів, зокрема вона випускає два види збірних книжкових полиць — А та В. Полиці обох видів виготовляють на верстатах 1 та 2. Тривалість обробки деталей однієї полиці кожної моделі подано в табл. (2.4).

Таблиця 2.4

ТРИВАЛІСТЬ ВИГОТОВЛЕННЯ КНИЖКОВИХ ПОЛИЦЬ

Верстат	Тривалість обробки полиці моделі, хв.	Ресурс робочого часу верстатів, год. на тиждень
А	В

Прибуток фірми від реалізації однієї полиці моделі А дорівнює 50 у. о., а моделі В — 30 у. о. Вивчення ринку збуту показало, що тижневий попит на книжкові полиці моделі А ніколи не перевищує попиту на модель В більш як на 30 одиниць, а продаж полиць моделі В не перевищує 80 одиниць на тиждень.

Необхідно визначити обсяги виробництва книжкових полиць цих двох моделей, що максимізують прибуток фірми. Для цього слід побудувати економіко-математичну модель поставленої задачі та розв’язати її графічно.

Побудова математичної моделі. Змінними в моделі є тижневі обсяги виробництва книжкових полиць моделей А та В. Нехай х₁ — кількість полиць моделі А, виготовлених фірмою за тиждень, а х₂ — кількість полиць моделі В. Цільова функція задачі — максимум прибутку фірми від реалізації продукції. Математично вона подається так:

.

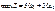Обмеження задачі враховують тривалість роботи верстатів 1 та 2 для виготовлення продукції та попит на полиці різних моделей.

Обмеження на тривалість роботи верстатів 1 та 2 мають вид:

для верстата 1:

30х₁ + 15х х₂ ≤ 2400 (хв);

для верстата 2:

12 х₁ + 26 х₂ ≤ 2160 (хв).

Обмеження на попит записуються так:

х₁ – х2 ≤ 30 та х₂ ≤ 80.

Загалом економіко-математичну модель цієї задачі можна записати так:

max Z = 50 х₁ + 30 х₂ (2.20)

за умов:

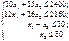
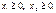
Ця економіко-математична модель є моделлю задачі лінійного програмування, що містить лише дві змінні, і тому може бути розв’язана графічно.

Розв’язання. Перший крок згідно з графічним методом полягає в геометричному зображенні допустимих планів задачі, тобто у визначенні такої області, де водночас виконуються всі обмеження моделі. Замінимо знаки нерівностей на знаки строгих рівностей і побудуємо графіки відповідних прямих (рис. 2.14). Кожна з побудованих прямих поділяє площину системи координат на дві півплощини. Координати точок однієї з півплощин задовольняють розглядувану нерівність, а іншої — ні. Щоб визначити необхідну півплощину (на рис. 2.14 її напрям позначено стрілкою), потрібно взяти будь-яку точку і перевірити, чи задовольняють її координати зазначене обмеження. Якщо задовольняють, то півплощина, в якій міститься вибрана точка, є геометричним зображенням нерівності. Інакше таким зображенням є інша півплощина.

Рис. 2.14

Умова невід’ємності змінних х₁ ≥ 0, х₂ ≥ 0 обмежує область допустимих планів задачі першим квадрантом системи координат. Переріз усіх півплощин визначає область допустимих планів задачі — шестикутник OABCDE. Координати будь-якої його точки задовольняють систему обмежень задачі та умову невід’ємності змінних. Тому поставлену задачу буде розв’язано, якщо ми зможемо відшукати таку точку багатокутника OABCDE, в якій цільова функція Z набирає найбільшого значення.

Для цього побудуємо вектор , координатами якого є коефіцієнти при змінних у цільовій функції задачі. Вектор завжди виходить із початку координат і напрямлений до точки з координатами (х₁ = с1; х₂ = с2). У нашій задачі вектор . Він задає напрям збільшення значень цільової функції Z, а вектор, протилежний йому, — напрям їх зменшення.

Побудуємо лінію, що відповідає, наприклад, значенню Z = 0. Це буде пряма 50 х₁ + 30 х₂ = 0, яка перпендикулярна до вектора і проходить через початок координат. Оскільки в даному прикладі необхідно визначити найбільше значення цільової функції, то пересуватимемо пряму 50 х₁ + 30 х₂ = 0 паралельно самій собі згідно з напрямом вектора 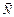доти, доки не визначимо вершину багатокутника, яка відповідає оптимальному плану задачі.

Із рис. 2.14 видно, що останньою спільною точкою прямої цільової функції та багатокутника OABCDE є точка С. Координати цієї точки є оптимальним планом задачі, тобто такими обсягами виробництва книжкових полиць видів А та В, що забезпечують максимум прибутку від їх реалізації за даних умов.

Координати точки С є розв’язком системи рівнянь (2.17) і (2.18):

звідси маємо: х₁ = 50; х₂ = 60.

Отже, Х* = (50; 60); Мах. Z = 50*50 + 30*60 = 4300

Це означає, що коли фірма щотижня виготовлятиме 50 збірних книжкових полиць моделі А та 60 — моделі В, то вона отримає максимальний прибуток — 4300 у. о. Це потребуватиме повного використання тижневих ресурсів робочого часу верстатів 1 та 2.

Задача 2.8.