 |
|
Розв’язування зведенням до задачі лінійного програмування
Нехай потрібно розв’язати задачу (7.1)—(7.3).
Позначимо 
і введемо заміну змінних  . Тоді цільова функція (7.1) матиме вигляд:
. Тоді цільова функція (7.1) матиме вигляд:
 Отримали цільову функцію, що виражена лінійною залежністю. Оскільки
Отримали цільову функцію, що виражена лінійною залежністю. Оскільки  , то звідси маємо:
, то звідси маємо:  . Підставимо виражені через нові змінні значення
. Підставимо виражені через нові змінні значення  в систему обмежень (7.2):
в систему обмежень (7.2):

Крім того, з початкової умови
 Умова (7.3) стосовно невід’ємності змінних набуває вигляду:
Умова (7.3) стосовно невід’ємності змінних набуває вигляду:
 .
.
Виконані перетворення приводять до такої моделі задачі:



Отримали звичайну задачу лінійного програмування, яку можна розв’язувати симплексним методом.
Допустимо, що оптимальний розв’язок останньої задачі існує і позначається:
 .
.
Оптимальні значення початкової задачі (7.1)—(7.3) визначають за формулою:

 .
.
Задачі нелінійного програмування.
Задача№1
Знайти мінімальне і максимальне значення функції:

за умов:
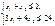
 .
.
Розв’язання. Область допустимих розв’язків утворює чотирикутник АВСD (рис. 8.1).

Геометрично цільова функція являє собою коло з центром у точці М (2; 2), квадрат радіуса якого  . Це означає, що її значення буде збільшуватися (зменшуватися) зі збільшенням (зменшенням) радіуса кола. Проведемо з точки М кола різних радіусів. Функція Z має два локальних максимуми: точки В (0; 6) і С (8; 0). Обчислимо значення функціонала в цих точках:
. Це означає, що її значення буде збільшуватися (зменшуватися) зі збільшенням (зменшенням) радіуса кола. Проведемо з точки М кола різних радіусів. Функція Z має два локальних максимуми: точки В (0; 6) і С (8; 0). Обчислимо значення функціонала в цих точках:
 ,
,
 .
.
Оскільки  , то точка С (8; 0) є точкою глобального максимуму.
, то точка С (8; 0) є точкою глобального максимуму.
Очевидно, що найменший радіус 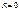 , тоді:
, тоді:
 . Тобто точка М є точкою мінімуму, оскільки їй відповідає найменше можливе значення цільової функції.
. Тобто точка М є точкою мінімуму, оскільки їй відповідає найменше можливе значення цільової функції.
Зазначимо, що в даному разі точка, яка відповідає оптимальному плану задачі (мінімальному значенню функціонала), знаходиться всередині багатокутника допустимих розв’язків, що в задачах лінійного програмування неможливо.
Задача№2
Знайти мінімальне значення функції:

за умов:

 .
.
Розв’язування. У даному прикладі множина допустимих розв’язків складається з двох окремих частин, необмежених зверху (рис. 8.2). Цільова функція аналогічно попередньому випадку є колом з центром у точці М (4; 4). Функція Z має два локальних мінімуми: в точці А ( 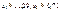 ), і в точці В (
), і в точці В (  ).
).

Значення функціонала в цих точках однакове і дорівнює:
 .
.
Отже, маємо два альтернативні оптимальні плани.
Задача №3
Акціонерне товариство з обмеженою відповідальністю виділило 1200 га ріллі під основні сільськогосподарські культури — озиму пшеницю і цукрові буряки.
У табл. 8.1 маємо техніко-економічні показники вирощування цих культур:
Таблиця 8.1
| Показник | Озима пшениця х1, сотні га | Цукрові буряки х2, сотні га |
| Урожайність, т/га | ||
| Ціна, грн/т | ||
| Собівартість, грн/т | 
| 
|
Необхідно знайти оптимальні площі посіву озимої пшениці та цукрових буряків.
Нехай: х1 — площа ріллі під озимою пшеницею, сотні га;
х2 — площа ріллі під цукровими буряками, сотні га.
Звернемо увагу на те, що собівартість тонни пшениці та цукрових буряків залежить від відповідної площі посіву.
Запишемо економіко-математичну модель цієї задачі. Критерієм оптимальності візьмемо максимізацію чистого доходу:

за умов:

Запишемо функцію Лагранжа:
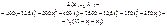
Візьмемо частинні похідні і прирівняємо їх до нуля:

З цієї системи рівнянь визначаємо координати сідлових точок. З першого та другого рівняння знаходимо l1 і, прирівнюючи вирази, маємо:
 (8.10)
(8.10)
або, скоротивши на 100 обидві частини і розкривши дужки, отримаємо:
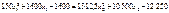
(8.11)
Із останнього рівняння системи маємо:  .
.
Підставимо вираз для  у рівність (8.11). Отримаємо:
у рівність (8.11). Отримаємо:

або
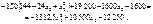

Отже,  ;
;

 .
.
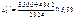 (553 га);
(553 га);
 (178 га).
(178 га).
Відповідно дістаємо:
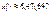 га);
га);
 га).
га).
Тобто отримали дві сідлові точки:


Перевіримо за допомогою достатньої умови існування екстремуму спочатку сідлову точку  .
.
Матриця Гессе має такий вигляд:
 .
.
За вищезазначеним правилом визначаємо головні мінори, починаючи з 2-го порядку (  ):
):
 ,
,
 .
.
Отже, головні мінори утворюють знакозмінний ряд та, починаючи з головного мінору 2-го порядку, наступний мінор визначається знаком  , тобто
, тобто  є точкою максимуму.
є точкою максимуму.
Обчислимо значення цільової функції в цій точці:

Аналогічні обчислення для точки  показують, що вона не є екстремальною.
показують, що вона не є екстремальною.
Отже, цільова функція набуде максимального значення, якщо озима пшениця вирощуватиметься на площі 647 га, а цукрові буряки — на площі 553 га.
Задача№4
Визначити вид квадратичної форми:

Матриця С має вигляд:
 .
.
Запишемо характеристичне рівняння
 .
.
Звідси маємо:


 .
.
Коренями отриманого квадратного рівняння є:  , тоді
, тоді  . Отже, квадратична форма
. Отже, квадратична форма  за теоремою 8.5 є напіввід’ємною.
за теоремою 8.5 є напіввід’ємною.
Задача№5
Підприємство виробляє два види продукції (А і В) і використовує на виробництво три види ресурсів: І, ІІ, ІІІ. Витрати ресурсів на виробництво одиниці кожного виду продукції подано в табл. 8.2.
Таблиця 8.2
| Вид ресурсу | Вид продукції | Загальний обсяг ресурсу | |
| А | В | ||
| І | |||
| ІІ | |||
| ІІІ |
Ціна реалізації одиниці продукції виду А становить 20 ум. од., проте прибуток залежить від витрат на виробництво, які пропорційні квадрату кількості виготовленої продукції. Аналогічно визначається прибуток для продукції виду В, ціна реалізації якої дорівнює 18 ум. од.
Розв’язання. Позначимо через х1 кількість продукції виду А, х2 — кількість продукції виду В, тоді загальний прибуток матиме вигляд: 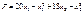 .
.
Математична модель задачі має вигляд:
 ,
,

 .
.
Розв’яжемо задачу методом Франка Вульфа.
І ітерація
Вибираємо точку, що належить множині допустимих планів задачі. Розглянемо, наприклад, точку  .
.
Визначимо градієнт цільової функції:
 .
.
В точці  обчислюємо значення градієнта:
обчислюємо значення градієнта:
 .
.
Використовуючи розраховане значення градієнта, записуємо і вводимо нову цільову функцію:  . Маємо таку задачу лінійного програмування:
. Маємо таку задачу лінійного програмування:


 .
.
Розв’язуючи цю задачу симплексним методом, знаходимо її оптимальний план:  .
.
Знайдемо новий допустимий план задачі, використовуючи формулу  для визначення координат наступної точки.
для визначення координат наступної точки.
Визначаємо координати точки Х1:
 ,
,  ,
,
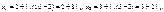
Знайдемо крок 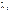 такий, за якого досягається максимальне значення цільової функції. Для цього підставимо розраховані значення для х1, х2, які виражені через
такий, за якого досягається максимальне значення цільової функції. Для цього підставимо розраховані значення для х1, х2, які виражені через  , у цільову функцію
, у цільову функцію  :
:

Отримали функцію, що залежить від  . Знайдемо значення
. Знайдемо значення  , за якого функція досягає максимуму, тобто коли її похідна дорівнює нулю:
, за якого функція досягає максимуму, тобто коли її похідна дорівнює нулю:
 Оскільки
Оскільки  , то беремо
, то беремо  . Тоді наступна точка Х1 має координати:
. Тоді наступна точка Х1 має координати:
 .
.
Для знайденої точки  обчислюємо значення цільової функції:
обчислюємо значення цільової функції: 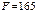 .
.
ІІ ітерація
Узявши точку  , обчислюємо значення градієнта в ній:
, обчислюємо значення градієнта в ній:

Використовуючи розраховане значення градієнта, вводимо нову цільову функцію:  . Отримуємо таку задачу лінійного програмування:
. Отримуємо таку задачу лінійного програмування:


 .
.
Розв’язавши її симплексним методом, отримуємо оптимальний план:  .
.
За формулою  визначаємо координати наступної точки наближення.
визначаємо координати наступної точки наближення.
Визначаємо координати точки Х2:

 ,
,
 Знайдемо такий крок λ2, за якого досягається максимальне значення цільової функції:
Знайдемо такий крок λ2, за якого досягається максимальне значення цільової функції:

Матимемо 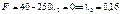 .
.
Обчислимо координати наступної точки Х2:

Для знайденої точки  значення цільової функції дорівнює:
значення цільової функції дорівнює:  .
.
Продовжуючи процес у аналогічний спосіб, на ІІІ ітерації визначаємо точку  і переконуємося, що значення цільової функції знову зростає:
і переконуємося, що значення цільової функції знову зростає:  .
.
На IV ітерації розраховуються координати точки  , для якої
, для якої  .
.
V ітерація
Узявши точку  , обчислюємо значення градієнта в ній:
, обчислюємо значення градієнта в ній:
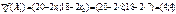 .
.
Використовуючи значення цього вектора (градієнта), вводимо нову цільову функцію:  і маємо таку задачу лінійного програмування:
і маємо таку задачу лінійного програмування:
 ,
,

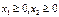 .
.
Розв’язавши цю задачу, отримаємо значення оптимального плану  , тобто повертаємося до попереднього значення. Отже, точку з координатами
, тобто повертаємося до попереднього значення. Отже, точку з координатами  вважаємо оптимальним планом, оскільки маємо нульовий градієнт функції, тобто цей план поліпшити вже не можна.
вважаємо оптимальним планом, оскільки маємо нульовий градієнт функції, тобто цей план поліпшити вже не можна.
12. Розв’язати графічним методом наступну задачу дробово-лінійного програмування:

за умов

Розв’язання:
2x1 + 4x2 = 16
x1 = 0, x2 = 4
x1 = 8, x2 = 0
-4x1 + 2x2 = 8
x1 = 0, x2 = 4
x1 = -2, x2 = 0
x1 + 3x2 = 9
x1 = 0, x2 = 3
x1 = 9, x2 = 0
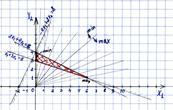
(d1c2 - d2c1) = 1 · (-2) - 2 · 3 = -8 < 0
max:

min:
