 |
|
АНАЛІЗ ЛІНІЙНИХ МОДЕЛЕЙ ЕКОНОМІЧНИХ ЗАДАЧ
Задача 4.1 Деяке підприємство виробляє чотири види продукції А, В, С, і D, використовуючи для цього три види ресурсів 1, 2 і 3. Норми витрат ресурсів на виробництво одиниці кожного виду продукції (в умовних одиницях) наведено в табл. 4.1.
Таблиця 4.1
Норми витрат ресурсів на виробництво продукції, ум. од.
| Ресурс | Норма витрат ресурсу на одиницю продукції виду | Запас ресурсу | |||
| А | В | С | D | ||
Відомі також ціни реалізації одиниці продукції кожного виду: для продукції А — 2 ум. од., для продукції В і D — по 4 ум. од., для продукції С — 3 ум. од.
Необхідно визначити оптимальний план виробництва продукції кожного виду за умов обмеженості запасів ресурсів, який дав би змогу підприємству отримати найбільшу виручку від реалізації продукції.
Розв’язання. Математичні моделі прямої (4.7) та двоїстої (4.8) задач мають такий вигляд:
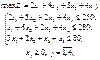 (4.7)
(4.7)
де хj — обсяг виробництва продукції j-го виду 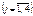 ;
;
 (4.8)
(4.8)
де yi — оцінка одиниці і-го виду ресурсу 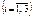 .
.
Симплексна таблиця, що відповідає оптимальному плану сформульованої вище задачі має вигляд:
| Базис | Сбаз | План | |||||||
| х1 | х2 | х3 | х4 | х5 | х6 | х7 | |||
| х4 | –2 | 1/2 | 1/2 | –1 | |||||
| х6 | –1 | –1 | |||||||
| х3 | 3/2 | –1/2 | |||||||
| Zj – cj ³ 0 | 5/2 | 1/2 |
Задача 4.2 Фірма виготовляє продукцію трьох видів: А, В і С. Потрібний певний час для обробки одиниці кожного виду продукції на різному обладнанні (табл. 4.2).
Таблиця 4.2
Тривалість обробки продукції, год
| Тип обладнання | Тривалість обробки одиниці продукції виду | Тривалість роботи обладнання на місяць | ||
| А | В | С | ||
| І | ||||
| ІІ | ||||
| ІІІ |
Ціна одиниці продукції видів А, В і С дорівнює 90 дол., 110 дол. та 150 дол. відповідно. Визначити, яку продукцію і в якому обсязі слід виготовляти, щоб фірма отримувала найбільший дохід.
Розв’язавши цю задачу симплекс-методом, отримаємо таку останню симплексну таблицю:
| Базис | Сбаз | План | ||||||
| х1 | х2 | х3 | х4 | х5 | х6 | |||
| х4 | –1/2 | |||||||
| х2 | –1 | 1/2 | –1 | |||||
| х1 | –1/2 | |||||||
| Fj – cj ³ 0 | 20 600 |
Керівництво фірми цікавить відповідь на таке запитання: «Чи зміниться оптимальний план виробництва продукції і якщо зміниться, то яким буде новий оптимальний план у кожній з наведених нижче ситуацій?»
1. Фірма може збільшити тривалість роботи обладнання типів 2 та 3 відповідно на 100 і 80 год на місяць, орендуючи для цього додаткове обладнання, але орендна плата становитиме 5000 дол. Чи вигідно це? Якщо вигідно, то яким має бути новий оптимальний план виробництва продукції?
2. Фінансовий відділ фірми вважає, що загострення конкуренції на ринку збуту може призвести до зниження ціни на продукцію В на 25 дол. Як це позначиться на оптимальному плані виробництва продукції фірми?
3. Відділ досліджень і розробок фірми пропонує виготовляти дешевшу модифікацію продукції С. Тривалість обробки одиниці цієї нової продукції на обладнанні типів 1, 2 та 3 становить відповідно 4, 3 і 1 год. Орієнтовна ціна одиниці нової продукції дорівнює 120 дол. Керівництво фірми цікавить, чи буде за таких умов виробництво нової продукції вигідним.
4. Споживач продукції виду А за певних обставин порушив попередню домовленість і відмовився прийняти більш як 100 од. продукції. Визначити, як слід змінити план виробництва своєї продукції, щоб уникнути втрат, пов’язаних із надвиробництвом цього виду продукції.
Розв’язання. Із наведеної в умові задачі симплекс-таблиці маємо: Х* = (180; 40; 0; 100; 0; 0),
max F = 20600, Y* = (0; 10; 70). Оптимальним планом виробництва продукції на фірмі є випуск 180 од. продукції виду А та 40 од. продукції виду В. Виготовлення продукції виду С не передбачається. При цьому фірма отримає максимальну виручку обсягом 20600 дол. на місяць.
1. Збільшення тривалості роботи обладнання дасть змогу збільшити випуск продукції, тобто змінити оптимальний план і дохід фірми. Оскільки Db1 = 0, Db2 = 100, Db3 = 80, то новий оптимальний план визначається так:
 .
.
Новий план допустимий (всі хj ³ 0), і тому оптимальні значення двоїстих оцінок зберігаються: Y* = (0; 10; 70). Приріст доходу фірми в результаті зміни оптимального плану виробництва продукції розраховується так:
max DZ = Db1y1 + Db2y2 + Db3y3 = 100 ∙ 10 + 80 ∙ 70 = 6600 дол.
Оскільки дохід фірми від додаткового використання обладнання груп 2 і 3 перевищує витрати на його оренду (6600 > 5000), то природно, що така тактика фірми буде вигідною. При цьому оптимальним планом виробництва стане випуск 290од. продукції виду А і 10 од. продукції виду В. Невикористаний час роботи обладнання типу І зменшиться до 50 год на місяць, а дохід фірми за відрахуванням витрат на оренду обладнання дорівнюватиме 20600 + (6600 – 5000) = 22200 дол. на місяць.
2. Зниження ціни одиниці продукції В на Dc2 (–25 дол.) стосується всього оцінкового рядка симплекс-таблиці, оскільки х2 є базисною змінною. Нові Fj – cj матимуть такі значення:
F3 – c3 = 10 – 1Dc2 = 10 + 25 = 35;
F5 – c5 = 10 + 1/2Dc2 = 10 – 12,5 = –2,5;
F6 – c6 = 70 – 1Dc2 = 70 + 25 = 95.
Якби всі здобуті оцінки задовольняли умову Zj – Cj ³ 0, то це означало б, що попри зниження ціни план виробництва продукції на фірмі не зміниться. Але оцінка F5 – c5 не задовольняє умову оптимальності задачі на максимум, і тому можна висновувати, що істотне зниження ціни одиниці продукції виду В порушує визначений раніше оптимальний план виробництва продукції, оскільки випуск цієї продукції стає для фірми невигідним, нерентабельним.
Новий оптимальний план визначається у процесі подальшого розв’язання задачі симплекс-методом:
| Базис | Сбаз | План | ||||||
| х1 | х2 | х3 | х4 | х5 | х6 | |||
| х4 | –1/2 | |||||||
 х2 х2
| –1 | 1/2 | –1 | |||||
| х1 | –1/2 | |||||||
| Fj – cj ³ 0 | 19 600 | –2,5 | ||||||
| х4 | –1 | |||||||
| х5 | –2 | –2 | ||||||
| х1 | ||||||||
| Fj – cj ³ 0 | 19 800 |
Отже, у розглянутій ситуації зниження ціни одиниці продукції виду В на 25 дол. різко змінить структуру та обсяги виробництва продукції на фірмі. Вигідним стане випуск лише продукції виду А обсягом 220 од.: при цьому можливий час роботи обладнання типів 1 та 2 використовуватиметься не повністю. Усе це призведе до зменшення виручки фірми до 19 800 дол. на місяць.
3. Обсяг виробництва нової продукції в оптимальному плані позначимо через х7. Тоді математична модель прямої задачі матиме такий вигляд:

У математичній моделі двоїстої задачі змінній х7 відповідатиме таке обмеження:  . Оцінимо рентабельність виробництва нової продукції за допомогою двоїстих оцінок: 4 · 0 + 3 · 10 + 1 · 70 = 100, що є меншим за 120. Отже, загальна вартість усіх ресурсів, що витрачаються на випуск одиниці нової продукції, не перевищує орієнтовної ціни цієї продукції, і тому її виробництво для фірми є вигідним, рентабельним. Завдяки цьому визначений раніше оптимальний план виробництва продукції можна поліпшити за рахунок уведення в нього х7.
. Оцінимо рентабельність виробництва нової продукції за допомогою двоїстих оцінок: 4 · 0 + 3 · 10 + 1 · 70 = 100, що є меншим за 120. Отже, загальна вартість усіх ресурсів, що витрачаються на випуск одиниці нової продукції, не перевищує орієнтовної ціни цієї продукції, і тому її виробництво для фірми є вигідним, рентабельним. Завдяки цьому визначений раніше оптимальний план виробництва продукції можна поліпшити за рахунок уведення в нього х7.
Для цього за допомогою оберненої матриці необхідно визначити елементи стовпчика «х7» останньої симплекс-таблиці:

Результати однієї ітерації симплекс-методу, що приводить до нового оптимального плану задачі, наведено нижче.
| Базис | Сбаз | План | q | |||||||
| х1 | х2 | х3 | х4 | х5 | х6 | х7 | ||||
 х4 х4
| –1/2 | 5/2 | ||||||||
| х2 | –1 | 1/2 | –1 | 1/2 | ||||||
| х1 | –1/2 | 1/2 | ||||||||
| Fj – cj ³ 0 | 20 600 | –20 | ||||||||
| х7 | 6/5 | 2/5 | –1/5 | |||||||
| х2 | –8/5 | –1/5 | 3/5 | –1 | ||||||
| х1 | 12/5 | –1/5 | –2/5 | |||||||
| Fj – cj ³ 0 | 21 400 |
Отже, оптимальним планом є Х* = (160; 20; 0; 0; 0; 0; 40), а max Z = 21 400. Керівництво фірми має підтримати пропозицію відділу досліджень та розробок і налагодити виробництво нової продукції, яка є рентабельною. Виготовляючи її обсягом 40 од., а також продукцію видів А та В обсягом 160 і 20 од. відповідно, фірма зможе збільшити обсяг виручки до 21400 дол. на місяць згідно з новим оптимальним планом виробництва продукції.
4. Четверта запропонована ситуація математично пов’язана із введенням в умову задачі додаткового обмеження, що може привести до таких наслідків:
а) нове обмеження для визначеного оптимального плану виконується. Тоді воно є надлишковим, зайвим і його включення до моделі не змінює визначеного плану;
б) нове обмеження для визначеного оптимального плану не виконується, і тоді за допомогою двоїстого симплекс-методу необхідно знайти новий оптимальний план.
За умовою задачі додатковим є обмеження х1 < 100. Але воно суперечить оптимальному обсягу продукції виду А, що дорівнює 180 од. Тому необхідно приєднати це додаткове обмеження до симплекс-таблиці та продовжити розв’язання задачі, але вже за допомогою двоїстого симплекс-методу. Для цього спочатку зведемо додаткове обмеження до канонічного вигляду:
х1 + х7 = 100.
Оскільки в оптимальному плані змінна х1 є базисною, то її необхідно записати через небазисні невідомі. Це робиться так. У симплекс-таблиці, яку наведено в умові задачі, рядок змінної «х1» подається рівнянням:
1 · х1 + 0 · х2 + 3 · х3 + 0 · х4 – 1/2 · х5 + 2 · х6 = 180.
З нього запишемо вираз для х1:
х1 = 180 – 3х3 + 1/2х5 – 2х6.
Підставивши цей вираз в додаткове обмеження, отримаємо:
180 – 3х3 + 1/2х5 – 2х6 + х7 = 100
або
– 3х3 + 1/2х5 – 2х6 + х7 = – 80.
| Базис | Сбаз | План | |||||||
| х1 | х2 | х3 | х4 | х5 | х6 | х7 | |||
| х4 | –1/2 | ||||||||
| х2 | –1 | 1/2 | –1 | ||||||
| х1 | –1/2 | ||||||||
 х7 х7
| – 80 | –3 | 1/2 | –2 | |||||
| Fj – cj ³ 0 | 20 600 | ||||||||
| х4 | –2 | ||||||||
| х2 | 200/3 | 1/3 | –1/3 | –1/3 | |||||
| х1 | |||||||||
| х3 | 80/3 | –1/6 | 2/3 | –1/3 | |||||
| Fj – cj ³ 0 | 61 000/3 | 35/3 | 190/3 | 10/3 |
У такому вигляді додаткове обмеження допишемо в симплекс-таблицю. Застосування двоїстого симплекс-методу приведе до нового оптимального плану задачі.
В останній таблиці маємо: Х* = (100; 200/3; 80/3; 20; 0;0), а
max Z = 61000/3 » 20333.
Проаналізуємо цей план. Прийнявши до уваги ситуацію, що склалася, керівництво фірми змушене змінити структуру виробництва продукції. Тепер з урахуванням вимог споживача фірма виготовлятиме 100 од. продукції виду А, 200/3 од. продукції виду В і 80/3 од. продукції виду С. У результаті такого плану випуску продукції виручка фірми дещо зменшиться (до 20333 дол. на місяць).
Транспортна задача
Компанія контролює три фабрики А1, А2, А3, здатні виготовляти відповідно 150, 60 та 80 тис. од. продукції щотижня. Вона уклала договір із чотирма замовниками В1, В2, В3, В4, яким потрібно щотижня доставляти відповідно 110, 40, 60 та 80 тис. од. продукції. Вартість транспортування 1000 од. продукції замовникам з кожної фабрики наведена в табл. 5.10.
| Фабрика | Вартість транспортування 1000 од. продукції замовнику | |||
| В1 | В2 | В3 | В4 | |
| А1 | ||||
| А2 | ||||
| А3 |
Визначити оптимальний план перевезень продукції від кожної фабрики до замовників, що мінімізує загальну вартість транспортних послуг.
Побудова математичної моделі. Нехай xij — кількість продукції, що перевозиться з і-ї фабрики до j-го замовника  . Оскільки транспортна задача за умовою є збалансованою, закритою
. Оскільки транспортна задача за умовою є збалансованою, закритою 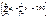
то математична модель задачі матиме вигляд:

Економічний зміст записаних обмежень полягає в тому, що вся вироблена на фабриках продукція має вивозитися до замовників повністю.
Аналогічні обмеження можна записати відносно замовників: продукція, що може надходити до споживача від трьох фабрик, має повністю задовольняти його попит. Математично це записується так:
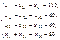
Загальні витрати, пов’язані з транспортуванням продукції, визначаються як сума добутків обсягів перевезеної продукції на вартості транспортування 1000 од. продукції до відповідного замовника і за умовою задачі мають бути мінімальними. Тому формально це можна записати так:
min Z = 4x11 + 4x12 + 2x13 + 5x14 + 5x21 + 3x22 + x23 + 2x24 + 2x31 +
+ x32 +4x33 +2x34.
Загалом математична модель сформульованої задачі має
вигляд:
min Z = 4x11 + 4x12 + 2x13 + 5x14 + 5x21 + 3x22 + x23 + 2x24 + 2x31 + x32 +
+ 4x33 +2x34
за умов:


Методи побудови опорного планц транспортної задачі.
Ідея методу північно-західного кута полягає в тому, що заповнення таблиці починають, не враховуючи вартостей перевезень, з лівого верхнього (північно-західного) кута.
Спочатку, не враховуючи вартості перевезень, завжди задовольняють потреби першого споживача В1, використовуючи запаси першого постачальника А1.
У нашому прикладі (табл. 5.2) потреби споживача В1 становлять 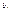 = 110, а запаси постачальника —
= 110, а запаси постачальника — 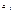 = 150 одиниць (тобто із запасів першого постачальника можна повністю задовольнити потреби першого споживача), тому в клітинку А1В1 записуємо менше із значень
= 150 одиниць (тобто із запасів першого постачальника можна повністю задовольнити потреби першого споживача), тому в клітинку А1В1 записуємо менше із значень 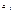 ,
,  , тобто 110.
, тобто 110.
Тепер потреби першого споживача повністю задоволені, і переходимо до задоволення потреб наступного (другого) споживача В2. Обсяг його потреб 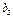 = 50. Після задоволення потреб першого споживача залишок запасів першого постачальника становить 150 –
= 50. Після задоволення потреб першого споживача залишок запасів першого постачальника становить 150 –
– 110 = 40. Отже, від першого виробника другому споживачеві можна перевезти лише 40 одиниць продукції, тому в клітину А1В2 записуємо число 40.
Після цього, оскільки запаси першого постачальника повністю вичерпані, переходимо до використання запасів наступного постачальника А2. Його запаси 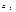 = 60, а незадоволені потреби другого споживача 50 – 40 = 10, тому в клітинку А2В2 записуємо число 10, і другий споживач у такий спосіб також повністю отримав необхідну кількість продукції. Переходимо до задоволення потреб наступного споживача В3.
= 60, а незадоволені потреби другого споживача 50 – 40 = 10, тому в клітинку А2В2 записуємо число 10, і другий споживач у такий спосіб також повністю отримав необхідну кількість продукції. Переходимо до задоволення потреб наступного споживача В3.
У результаті часткового використання запасів другого постачальника його залишок продукції становить 60 – 10 = 50. Отже, від другого виробника до третього споживача можна перевезти 50 одиниць продукції. Клітинка А2В3 міститиме зазначене число 50, і цим запаси постачальника А2 будуть повністю вичерпані.
Переходимо до розподілу запасів останнього (третього) постачальника А3. Залишились незадоволеними потреби третього споживача в обсязі 60 –50 = 10. Для їх задоволення скористаємося запасами постачальника А3. У клітинку А3В3 записуємо число 10, і потреби споживача В3 також повністю задоволені. Переходимо до останнього споживача В4 з потребами b4 = 80, які повністю задовольняються за рахунок залишку запасів третього постачальника: 90 – 10 = 80. Таблиця 5.2
| Постачальники | Запаси | Споживачі | |||
| B1 | B2 | B3 | B4 | ||
| Потреби | |||||
| b1 = 110 | b2 = 50 | b3 = 60 | b4 = 80 | ||
 А1 А1
| а1 = 150 | ||||
| А2 | а2 = 60 | ||||
| А3 | а3 = 90 |
Отже, в таблиці 5.2 у заповнених клітинках знаходяться числа, що означають можливий план перевезень продукції. Сума чисел (перевезень) по рядках дорівнює обсягам запасів постачальників, а сума чисел по стовпцях — обсягам потреб відповідних споживачів.
Визначимо загальну вартість перевезень згідно з початковим опорним планом. Від першого постачальника до першого споживача необхідно перевезти 110 одиниць продукції за ціною 4 ум. од. (ціна записана в правому верхньому куті кожної клітини), отже, це коштуватиме 110*4=440ум. од. Крім того, необхідно перевезти від першого постачальника 40 одиниць продукції до другого споживача за ціною 4 ум. од. і т. д. У такий спосіб визначимо загальну вартість усіх перевезень:
 (ум. од.).Записуємо оптимальний план, за допомогою матриці:
(ум. од.).Записуємо оптимальний план, за допомогою матриці: 
Ідея методу мінімальної вартості полягає в тому, що на кожному кроці заповнюють клітинку таблиці, яка має найменшу вартість перевезення одиниці продукції. Такі дії повторюють доти, доки не буде розподілено всю продукцію між постачальниками та споживачами.
Складемо за допомогою цього методу план розглянутої задачі (табл. 5.3).
Найменшу вартість мають перевезення, які здійснюються від А2 до В3 та від А3 до В2 (ціна перевезення одиниці продукції — 1 ум. од.). Заповнимо будь-яку з них, наприклад, А2В3. Оскільки постачальник має 60 одиниць продукції, а споживач потребує саме такої її кількості, то в клітину А2В3 ставимо значення 60. У такий спосіб запаси другого постачальника повністю вичерпані, а потреби третього споживача повністю задоволені.
Також мінімальною є вартість перевезень від третього постачальника до другого споживача, тому заповнимо також клітину А3В2.
З клітинок таблиці, що залишились незаповненими, вибираємо наступне мінімальне значення вартості перевезень, яке дорівнює
2 ум. од. — для клітин А1В3, А2В4, А3В1 та А3В4. Заповнення клітин А2В4 та А1В3 неможливе, оскільки постачальник А2 вже повністю вичерпав власний обсяг запасів, задовольняючи потреби споживача В3, а споживач В3 повністю задовольнив свої потреби. Отже, можна заповнити тільки клітину А3В1 чи А3В4. Заповнимо А3В1. Обсяг запасів а3 = 90, причому 50 одиниць продукції вже надано другому споживачеві. Отже, маємо залишок 90 – 50 = 40, а потреби b1 = 110, тому від третього постачальника до першого споживача плануємо перевезти 40 одиниць продукції. Тепер у клітину А3В4 не можна записати будь-який обсяг постачання, оскільки запаси третього постачальника вже повністю вичерпані.
Знову вибираємо найменшу вартість для клітин таблиці, що залишилися пустими, і продовжуємо процес доти, поки всі запаси не будуть розподілені, а потреби — задоволені.
Таблиця 5.3
| bj ai | b1 = 110 | b2 = 50 | b3 = 60 | b4 = 80 |
| а1 = 150 | ||||
| а2 = 60 | ||||
| а3 = 90 |
В результаті таких міркувань отримали початковий опорний план, загальна вартість перевезень для якого становить:
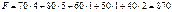 (ум. од.).
(ум. од.).
Значення цільової функції менше за попередній варіант, значить цей план ближчий до оптимального.
Метод подвійної переваги. Якщо розмірність задачі досить велика, то перебір за методом мінімальної вартості ускладнюється. В такому разі спростити пошук клітин з найменшими вартостями можна, застосовуючи метод подвійної переваги.
Згідно з процедурою цього методу перед початком заповнення таблиці необхідно позначити будь-якими символами клітинки, які містять найменшу вартість у рядках, а потім — у стовпчиках. Таблицю починають заповнювати з клітинок, позначених двічі (які містять вартості, що є мінімальними і в рядку, і в стовпчику). Далі заповнюють клітинки, позначені один раз (що містять мінімальні вартості або в рядку, або в стовпчику), а вже потім — за методом мінімальної вартості.
Таблиця 5.4
| bj ai | b1 = 110 | b2 = 50 | b3 = 60 | b4 = 80 |
| а1 = 150 | V 2 | |||
| а2 = 60 | VV 1 | V 2 | ||
| а3 = 90 | V 2 | VV 1 | V 2 |
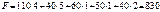 (ум. од.).
(ум. од.).
Застосування для побудови опорного плану даного методу уможливлює отримання найменшого у зіставленні з розглянутими вище значення цільової функції. Отже, такий план є найближчим до оптимального.
Дробово-лінійне програмування:
Розв’яжіть графічно задачу дробово-лінійного програмування:

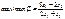
за умов:

 .
.
Розв’язання. Побудуємо на площині область допустимих розв’язків задачі. Маємо трикутник АВС.
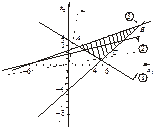
Рис. 7.1
Цільова функція задачі являє собою пряму, що обертається навколо початку системи координат (на рис. 7.1 позначена пунктиром). Отже, залежно від напрямку обертання точками максимуму та мінімуму будуть А і С.
Скористаємося правилами визначення максимального та мінімального значень цільової функції. Перевіримо умову
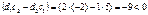 ,
,
тобто для будь-якого значення Z функція  є спадною (тому що <0), отже, зі зростанням Z кутовий коефіцієнт нахилу прямої, що виражає цільову функцію, зменшуватиметься, а тому відповідну пряму потрібно обертати навколо початку координат за годинниковою стрілкою.
є спадною (тому що <0), отже, зі зростанням Z кутовий коефіцієнт нахилу прямої, що виражає цільову функцію, зменшуватиметься, а тому відповідну пряму потрібно обертати навколо початку координат за годинниковою стрілкою.
1) якщо  , то функція є зростаючою. Тобто у разі, якщо
, то функція є зростаючою. Тобто у разі, якщо 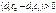 , для відшукання точки максимуму необхідно повертати пряму, що описує цільову функцію, навколо початку системи координат у напрямку проти годинникової стрілки;
, для відшукання точки максимуму необхідно повертати пряму, що описує цільову функцію, навколо початку системи координат у напрямку проти годинникової стрілки;
2)якщо 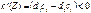 , то функція є спадною і за збільшення. Тому у разі, якщо
, то функція є спадною і за збільшення. Тому у разі, якщо 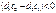 , для відшукання точки максимуму необхідно повертати пряму, що описує цільову функцію, навколо початку системи координат у напрямку за годинниковою стрілкою.
, для відшукання точки максимуму необхідно повертати пряму, що описує цільову функцію, навколо початку системи координат у напрямку за годинниковою стрілкою.
При розв’язуванні задачі дробово-лінійного програмування графічним методом можливі такі випадки:
- багатокутник розв’язків задачі обмежений і максимальне та мінімальне значення досягаються у його кутових точках;
- багатокутник розв’язків задачі необмежений, однак існують кутові точки, в яких досягаються максимальне та мінімальне значення цільової функції;
- багатокутник розв’язків задачі необмежений і досягається лише один із екстремумів;
- багатокутник розв’язків задачі необмежений, точки екстремумів визначити неможливо.
Виконуючи зазначений порядок дій, маємо: С — точка максимуму, а точка А є точкою мінімуму цієї задачі. Знаходимо точку перетину відповідних прямих (точка максимуму чи мінімуму) і розв’язуємо систему рівнянь щодо цих прямих. Знаходимо x1 та x2, підставляємо в «Z»
5. У наведених далі задачах(Sensetive-аналіз):
а) побудуйте економіко-математичні моделі початкової й двоїстої задач;
б) приведіть задачі до канонічного виду й дайте економічне тлумачення основних й допоміжних змінних двох задач;
в) з наведеної останньої симплексної таблиці початкової задачі запишіть оптимальні плани  і
і  ;
;
г) визначте дефіцитні й недефіцитні ресурси, рентабельну та збиткову продукцію;
д) знайдіть межі зміни обсягів дефіцитних ресурсів, в котрих оцінка ресурсу залишається сталою (аналіз двоїстих оцінок на стійкість);
е) знайдіть межі зміни обсягів недефіцитних ресурсів;
є) знайдіть межі зміни цін на рентабельну і нерентабельну продукцію, в котрих структура оптимального плану початкової задачі не змінюється;
ж) в якому випадку розширення асортименту випуску за рахунок введення нової продукції буде доцільним, чи недоцільним?
5.1. Підприємство виготовляє три види продукції А, В і С, використовуючи для цього три види ресурсів I, II, III. Норми витрат усіх ресурсів на одиницю продукції та запаси ресурсів наведено в табл.1
Таблиця 1
| І II III |
Відома ціна одиниці продукції кожного виду: А - 9 ум.од., В -10 ум. од. і С - 16 ум.од. Визначити план виробництва продукції, що забезпечує підприємству найбільший доход.
Остання симплекс-таблиця даної задачімає такий вигляд
Розв’язок: Математична модель прямої та двоїстої задач мають вигляд:
а) Z= 

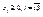
Де  - обсяг виробництва j –го виду.
- обсяг виробництва j –го виду.



Де y i - оцінка одиниці і-го виду ресурсу.
б) основні змінні  ,
,  ,
,  характеризують кількість продукції А, В, С, яку необхідно виготовляти. Додаткові змінні
характеризують кількість продукції А, В, С, яку необхідно виготовляти. Додаткові змінні  ,
, 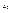 ,
,  - характеризують залишки відповідних ресурсів І, ІІ, ІІІ.
- характеризують залишки відповідних ресурсів І, ІІ, ІІІ.
в)  =(0,8,20,0,0,96)
=(0,8,20,0,0,96)
 = (2/9, 5/3, 0)
= (2/9, 5/3, 0)
г) відповідно до оптимального плану прямої задачі, необхідно виготовляти продукцію В і С у кількості відповідно 8 і 20 од, ці види продукції і будуть рентабельними. Випуск продукції а буде нерентабельним (  =0). І і ІІ ресурс використовуються повність, отже вони є дефіцитними, а ІІІ ресурс у процесі виробництва використовується неповністю і є недефіцитним.
=0). І і ІІ ресурс використовуються повність, отже вони є дефіцитними, а ІІІ ресурс у процесі виробництва використовується неповністю і є недефіцитним.
д) Дефіцитними є ресурси І та ІІ.
Математична постановка:

Приріст запасу першого ресурсу позначимо через 

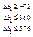
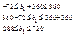
Приріст запасу другого ресурсу позначимо через 
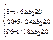


е) 
ж ) Дослідимо питання про доцільність введення нового n+1-го виду продукції.  - витрати кожного виду ресурсу на виготовлення одиниці такої продукції.
- витрати кожного виду ресурсу на виготовлення одиниці такої продукції.
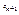 - ціна її реалізації.
- ціна її реалізації.
Обмеження, що описує витрати на виробництво нового виду продукції:

Рентабельною є продукція, для якої відповідне обмеження виконується як рівняння, а нерентабельною, якщо ліва частина нерівності(витрати ресурсів на виробництво одиниці продукції) перевищує праву (ціну реалізації одиниці продукції).
Розширення асортименту за рахунок нової продукції буде доцільним якщо витрати на виробництво продукції будуть менші, ніж ціна реалізації.
5.2 Підприємство виготовляє продукцію видів A, B, C для чого використовує три види ресурсів І, ІІ, ІІІ. Норми витрат усіх ресурсів на одиницю кожної продукції та обсяги ресурсів на підприємстві наведено в табл.. 1
Таблиця 1
| Вид ресурсу | Норма витрат на одиницю продукції за видами | Запас ресурсу | ||
| А | В | С | ||
| І II III |
Відома ціна одиниці продукції кожного виду: А - 10 ум.од., В -14 ум.од. і С - 12 ум.од. Визначити план виробництва продукції, що забезпечує підприємству найбільший доход. Остання симплекс-таблиця, що містить оптимальний план задачі, має такий вигляд (табл.2)
Розв’язок: Математична модель прямої та двоїстої задач мають вигляд:
а) Z= 
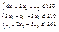

Де  - обсяг виробництва j –го виду.
- обсяг виробництва j –го виду.



Де y i - оцінка одиниці і-го виду ресурсу.
б) основні змінні  ,
,  ,
,  характеризують кількість продукції А, В, С, яку необхідно виготовляти. Додаткові змінні
характеризують кількість продукції А, В, С, яку необхідно виготовляти. Додаткові змінні  ,
, 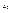 ,
,  - характеризують залишки відповідних ресурсів І, ІІ, ІІІ.
- характеризують залишки відповідних ресурсів І, ІІ, ІІІ.
в)  =(0,82,16,0,80,0)
=(0,82,16,0,80,0)
 = (23/4, 0, 5/4)
= (23/4, 0, 5/4)
г) відповідно до оптимального плану прямої задачі, необхідно виготовляти продукцію В і С у кількості відповідно 82 і 16 од, ці види продукції і будуть рентабельними. Випуск продукції А буде нерентабельним (  =0). І і ІІІ ресурси використовуються повність(
=0). І і ІІІ ресурси використовуються повність(  =
=  =0), отже вони є дефіцитними, а ІІІресурс у процесі виробництва використовується неповністю (
=0), отже вони є дефіцитними, а ІІІресурс у процесі виробництва використовується неповністю ( 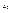 =80) і є недефіцитним.
=80) і є недефіцитним.
д) Дефіцитними є ресурси І та ІІІ.
Математична постановка:

Приріст запасу першого ресурсу позначимо через 



Приріст запасу третього ресурсу позначимо через 



е)
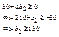
ж ) Дослідимо питання про доцільність введення нового n+1-го виду продукції.  - витрати кожного виду ресурсу на виготовлення одиниці такої продукції.
- витрати кожного виду ресурсу на виготовлення одиниці такої продукції.
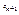 - ціна її реалізації.
- ціна її реалізації.
Обмеження, що описує витрати на виробництво нового виду продукції:

Рентабельною є продукція, для якої відповідне обмеження виконується як рівняння, а нерентабельною, якщо ліва частина нерівності(витрати ресурсів на виробництво одиниці продукції) перевищує праву (ціну реалізації одиниці продукції).
Розширення асортименту за рахунок нової продукції буде доцільним якщо витрати на виробництво продукції будуть менші, ніж ціна реалізації.