 |
|
Метод розв'язування задачі дрібно лінійного програмування у загальному вигляді.
Економічна і математична постановка задачі
Розв'язуючи економічні задачі, часто за критерій оптимальності беруть показники рентабельності, продуктивності праці тощо, які математично подаються дробово-лінійними функціями. Загальну економіко-математичну модель у цьому разі записують так:
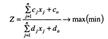
за умов
Припускають, що знаменник цільової функції в області допустимих розв'язків системи обмежень не дорівнює нулю.
Алгоритм розв'язування задачі дробово-лінійного програмування передбачає зведення її до задачі лінійного програмування. Щоб виконати таке зведення, позначимо
зробимо заміну змінних
і запишемо економіко-математичну модель:
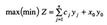
за умов
Дістали задачу лінійного програмування, яку можна розв'язати симплексним методом. Нехай оптимальний план
Оптимальні значення х0j знайдемо за формулою
Графічний метод
У разі, коли задача дробово-лінійного програмування містить лише дві змінні, для її розв’язування зручно скористатися графічним методом.
Нехай маємо таку задачу:
(7.4)
за умов:
(7.5)
, 
(7.6)
Спочатку, як і для звичайної задачі лінійного програмування будуємо геометричне місце точок системи нерівностей (7.5), що визначає деякий багатокутник допустимих розв’язків.
Допустимо, що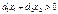 
, і цільова функція набуває деякого значення:
.
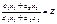Після елементарних перетворень дістанемо:
або 
. (7.7)
Останнє рівняння описує пряму, що обертається навколо початку системи координат залежно від зміни значень х1 та х2.
Розглянемо кутовий коефіцієнт нахилу прямої (7.7), що виражає цільову функцію:
. (7.8)
Отже, кутовий коефіцієнт являє собою функцію від Z. Для визначення умов зростання (спадання) функції (7.8) дослідимо зміну знака її похідної:
(7.9)
Використовуючи формулу (7.9), можна встановити правила пошуку максимального (мінімального) значення цільової функції:
1.) якщо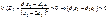 
,
то функція (7.8) є зростаючою, і за збільшення значення Z (значення цільової функції) кутовий коефіцієнт нахилу прямої (7.7) також збільшується. Тобто у разі, якщо 
, для відшукання точки максимуму необхідно повертати пряму, що описує цільову функцію, навколо початку системи координат у напрямку проти годинникової стрілки;
2.)якщо 
, то функція (7.8) є спадною і за збільшення значення Z (значення цільової функції) кутовий коефіцієнт нахилу прямої (7.7) буде зменшуватись. Тому у разі, якщо 
, для відшукання точки максимуму необхідно повертати пряму, що описує цільову функцію, навколо початку системи координат у напрямку за годинниковою стрілкою.
При розв’язуванні задачі дробово-лінійного програмування графічним методом можливі такі випадки:
-багатокутник розв’язків задачі обмежений і максимальне та мінімальне значення досягаються у його кутових точках;
-багатокутник розв’язків задачі необмежений, однак існують кутові точки, в яких досягаються максимальне та мінімальне значення цільової функції;
-багатокутник розв’язків задачі необмежений і досягається лише один із екстремумів;
-багатокутник розв’язків задачі необмежений, точки екстремумів визначити неможливо.