 |
|
СИСТЕМАТИЧНІ, ПРОГРЕСУЮЧІ ТА РЕГУЛЯРНІ ПОХИБКИ
Задача 17.Абсолютна систематична похибка задана граничними значеннями 
. Що означає цей запис?
Розв’язання. Це означає, що залишаючись сталою і невідомою, абсолютна систематична похибка знаходиться в межах
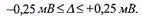
Під час повторних вимірювань ця похибка кожен раз буде набувати те саме значення із вказаного діапазону.
Задача 18. Граничне значення відносної систематичної похибки коефіцієнта підсилення підсилювача становить ± 0,02 %. Що означає цей запис?
Розв’язання. Це означає, що фактичне значення коефіцієнта підсилення конкретного значення коефіцієнта підсилення не більше ніж на 0,02 % в той чи інший бік. Тобто
Задача 19.Абсолютна похибка вольтметра на 
в режимі без калібрування може досягати значень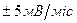 
. Що означає цей запис? Знайти допустимі зміни похибки за півмісяця.
Разв’язання. Це означає, то похибка вольтметра після останнього калібрування за один місяць в найгіршому випадку не перевищить значення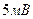 
в той чи інший бік.
За півмісяця слід очікувати систематичну похибку, не більшу за половину граничною значення, тобто за 
і т.д.
Задача 20.Відносна часова нестабільність резистора задана граничним значенням 
.
Що означає цей запис? Яка можлива максимальна зміна опору резистора за 5 років?
Розв’язання. Це означає, що за один рік експлуатації резистора його опір може змінитися не більше ніж на 
в той чи інший бік.
А за п’ять років експлуатації ця зміна в найгіршому випадку може досягати у п’ять разів більшого значення, тобто 
.
Важливим є те, що фактична зміна опору конкретного резистора без виконання додаткових досліджень залишається невідомою, однак обмеженою граничними значеннями.
ВИПАДКОВІ ПОХИБКИ
Задача 21.Випадкова похибка має рівномірний розподіл у межах від –5 мВ до +25 мВ. Визначити математичне сподівання похибки і записати розподіл похибки.
Розв’язання, 1. Математичне сподівання похибки становить
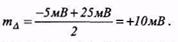
2. Висота прямокутника рівномірного розподілу обернена до розмаху розподілу
тому розподіл похибки
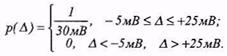
Задача 22.Випадкова похибка, як у прикладі 8.1, має рівномірний розподіл у межах від -5 мВ до +25 мВ. Визначити дисперсію та стандартне відхилення похибки.
Розв’язання. 1. Дисперсія похибки становить
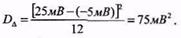
2. Стандартне відхилення дорівнює
Задача 23.Випадкова похибка має нормальний розподіл з параметрами 
, 
. Визначити її математичне сподівання, стандартне відхилення і дисперсію, записати розподіл похибки.
Розв'язання. 1. Відповідно до означення параметр т нормального розподілу є математичним сподіванням похибки, тому
2. Відповідно до означення параметр ст нормального розподілу є стандартним відхиленням похибки
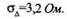
3. Дисперсія похибки дорівнює квадрату стандартного відхилення, тобто
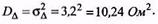
4.Відповідно до (8.8) 
вираз густини розподілу
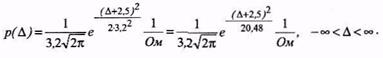
Задача 24.Випадкова похибка має рівномірний розподіл у межах від 
до 
. Визначити довірчі границі похибки для довірчої ймовірності 
.
Розв’язання. 1. Математичне сподівання похибки є нульовим
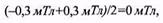
тобто розподіл є симетричним відносно початку координат.
2. Тому для такого рівномірного розподілу відношення довірчої границі 
до граничного значення 
безпосередньо дорівнює довірчій ймовірності
Звідси для та 
знаходимо довірчі границі :
Задача 25. Випадкова похибка має нормальний розподіл з параметрами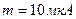 
, 
. Визначити довірчі границі похибки для та 
.
Розв’язання.
1.Відповідно до означення параметри т та а нормального розподілу є математичним сподіванням та стандартним відхиленням похибки, тому
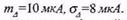
2.Відповідно до (8.13)
для заданих довірчих ймовірностей квантилі становлять відповідно:
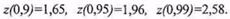
3.Відповідні довірчі границі похибки знайдемо за виразом (8.22) 
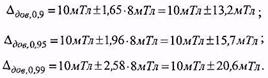
Задача 26. Відомі параметри нормального розподілу трьох складових похибки вимірювання опору:
Знайти математичне сподівання, дисперсію та стандартне відхилення сумарної похибки.
Розв’язання. 1. Математичне сподівання сумарної похибки дорівнює алгебраїчній сумі математичних сподівань складових
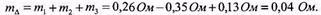
2. Дисперсія суми незалежних похибок дорівнює сумі їх дисперсій, а останні для нормального розподілу дорівнюють квадрату стандартного відхилення, тому
3. Стандартне відхилення сумарної похибки дорівнює квадратному кореню з дисперсії
Задача 27.Для умови і розв’язків прикладу 8.6 знайти довірчі границі похибки для 
.
Розв’язання 1. Для квантиль нормального розподілу 
.
2. Підставляючи отримане в прикладі 8.6 значення стандартного відхилення сумарної похибки у (8.33) 
, матимемо довірчі границі сумарної похибки
Задача 28. Відомі граничні значення незалежних рівномірно розподілених похибок
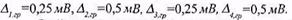
Знайти математичне сподівання, дисперсію та стандартне відхилення сумарної похибки.
Роїв 'язання, 1. Оскільки похибки задані лише своїм граничним значенням, то їх розподіл є симетричним відносно початку координат, тобто їх математичні сподівання є нульовими
Отже, математичне сподівання сумарної похибки також дорівнює нулеві.
2. Дисперсія суми незалежних похибок дорівнює сумі іх дисперсій, а останні для
рівномірного розподілу дорівнюють одній третій квадрата граничного значення, тому
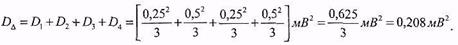
3. Стандарте відхилення сумарної похибки дорівнює квадратному кореню з дисперсії
Задача 29.Для умови і розв’язків задачі 28 знайти довірчі границі похибки для .
Розв'язання, 1. Для квантиль нормального розподілу 
.
2. Підставляючи отримане в задачі 28 значення стандартного відхилення сумарної похибки у (8.39)
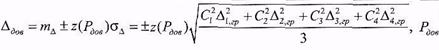, матимемо довірчі границі сумарної похибки
Задача 30. Три нормально розподілені випадкові похибки з нульовим математичним сподіванням та стандартними відхиленнями:
є статистично залежними, характеризуються взаємними коефіцієнтами кореляції
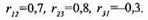
Знайти дисперсію та стандартне відхилення сумарної похибки і порівняти їх із значеннями, отриманими без урахування взаємної кореляції.
Розв’язання. 1. Використовуючи (8.45) для трьох складових похибки, визначимо дисперсію сумарної похибки
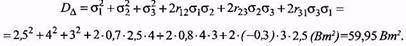
2. Стандартне відхилення сумарної похибки
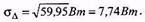
3. Дисперсія сумарної похибки без урахування кореляції похибок
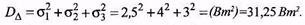
4. Стандартне відхилення сумарної похибки без урахування кореляції похибок
5. Отже, неврахування взаємної кореляції похибок призводить до того, що отримані таким способом дисперсія та стандартне відхилення сумарної похибки істотно відрізняються від їх справжніх значень.