 |
|
ІНСТРУМЕНТАЛЬНІ ПОХИБКИ
Задача 40.Нехай для певного ЗВТ регламентовані такі нормальні умови: температура від 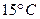 до
до 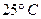 напруга живлення від
напруга живлення від  до
до 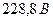 , з робоча область: температура від
, з робоча область: температура від 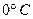 до
до 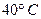 і напруга живлення від
і напруга живлення від 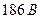 до
до 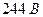 . Інші впливні величини для цього ЗВ не регламентовані. Цим ЗВТ в різний час було здійснено чотири вимірювання в різних умовах: 1) температура приміщення
. Інші впливні величини для цього ЗВ не регламентовані. Цим ЗВТ в різний час було здійснено чотири вимірювання в різних умовах: 1) температура приміщення 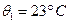 , напруга живлення —
, напруга живлення —  ; 2)
; 2)  ,
, 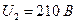 3)
3)  ,
, 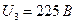 ; 4)
; 4)  ,
, 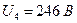 . Проаналізувати ці вимірювання відносно влливних величин.
. Проаналізувати ці вимірювання відносно влливних величин.
Розв’язання. 1. Перше вимірювання виконано у нормальних умовах, бо і температура (  ) і напруга живлення (
) і напруга живлення (  ) знаходяться в області нормальних значень, тому оцінюють лише основну похибку ЗВ.
) знаходяться в області нормальних значень, тому оцінюють лише основну похибку ЗВ.
2.У другому вимірюванні температура є в межах нормальної області ( 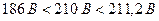 ), а напруга живлення вийшла за межі нормальної області, але у межах робочої (
), а напруга живлення вийшла за межі нормальної області, але у межах робочої ( 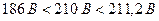 ), тому оцінюють основну та додаткову похибки від впливу зміни напруги живлення.
), тому оцінюють основну та додаткову похибки від впливу зміни напруги живлення.
3.У третьому вимірюванні температура вийшла за межі нормальної області, але у межах робочої ( 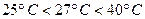 ), а напруга живлення в межах нормальної області (
), а напруга живлення в межах нормальної області (  ), тому оцінюють основну та додаткову температурні похибки.
), тому оцінюють основну та додаткову температурні похибки.
4.У четвертому вимірюванні температура вийшла за межі нормальної області, але в межах робочої (  ), а напруга живлення вийшла за межі робочої області (
), а напруга живлення вийшла за межі робочої області ( 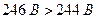 ), тому результат вимірювання є недостовірним і його не можна використати.
), тому результат вимірювання є недостовірним і його не можна використати.
Задача 41.Амперметр на  , класу точності 0,5. Встановити границі основної абсолютної похибки.
, класу точності 0,5. Встановити границі основної абсолютної похибки.
Розв’язання. Клас точності 0,5 означає, що границі основної (у нормальних умовах) допустимої зведеної (до  ) похибки становлять ± 0,5%. Тому відповідно до (10.4)
) похибки становлять ± 0,5%. Тому відповідно до (10.4)

незалежно від показу амперметра.
Задача 42.Для амперметра з прикладу 10.3 встановити границі основної відносної похибки, якщо показ амперметра 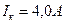 .
.
Розв’язання. 1-й спосіб. Використати границі абсолютної похибки з прикладу 10.3. Згідно з означенням границі відносної похибки дорівнюють відношенню границь абсолютної похибки до показу, тому
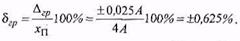
2-й спосіб. Безпосереднє застосування виразу (10.4), тобто

Отже, знайдені обома способами границі відносної похибки є однаковими.
Задача 43.Що означає клас точності 0,5/0,2 цифрового амперметра з границею вимірювання  ?
?
Розв’язання Клас точності 0,5/0,2 означає, що границі основної (у нормальних умовах) допустимої зведеної (до  ) похибки становлять: на початку діапазону (
) похибки становлять: на початку діапазону (  )
) 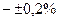 , і в кінці діапазону (
, і в кінці діапазону (  )
)  .
.
Задача 44.Для згадуваного у прикладі 10.5 амперметра обчислити граничне значення відносної похибки, якщо показ дорівнює третині діапазону і порівняти з граничною відносною похибкою аналогового амперметра.
Розв’язання. 1. Якщо показ дорівнює третині діапазону ( 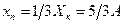 ), граничне значення відносної похибки дорівнює
), граничне значення відносної похибки дорівнює

2. При застосуванні аналогового амперметра 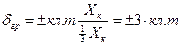 , що дає для амперметра на
, що дає для амперметра на  граничне значення відносної похибки
граничне значення відносної похибки

або на 60 % більше.
Задача 45.Адитивні границі похибки трьох цифрових вольтметрів пронормовані і І такими значеннями: 1 – ± 0,02 %оf FS; 2 – ± 50 ррm оf FS; 3 – ± 5 LSB. Для першого приладу :границя вимірювання становить 1V (  ), для другого 10V (
), для другого 10V (  ), а для третього 2V (
), а для третього 2V ( 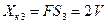 ), якщо кількість квантів у діапазоні
), якщо кількість квантів у діапазоні 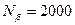 . Визначити границі і , абсолютних похибок вольтметрів.
. Визначити границі і , абсолютних похибок вольтметрів.
Розв’язання. 1. Відповідно до означень границі абсолютної адитивної похибки вольтметрів
першого —  ,
,
другого —  ,
,
третього — 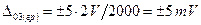 .
.
Задача 46.Мультиплікативні границі похибки згаданих вище цифрових вольтметрів пронормовані такими значеннями: 1) –  ; 2) –
; 2) – 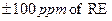 ; 3) –
; 3) –  . Покази приладів становили
. Покази приладів становили  , для другого
, для другого 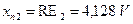 ,
,  . Визначити границі абсолютних похибок вольтметрів на вказаних показах.
. Визначити границі абсолютних похибок вольтметрів на вказаних показах.
Розв’язання. Відповідно до означення границі абсолютної мультиплікативної похибки вольтметрів
першого —  ,
,
другого — 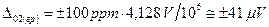 ,
,
третього —  .
.
Задача 47. У документації на прилад записано, що нормальні умови щодо температури 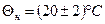 (від
(від 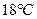 до
до  ), додаткова температурна похибка не перевищує основної на кожні
), додаткова температурна похибка не перевищує основної на кожні 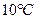 (
(  ) відхилення температури від нормальної області. Вимірювання виконувались при температурі в приміщенні, де знаходився прилад
) відхилення температури від нормальної області. Вимірювання виконувались при температурі в приміщенні, де знаходився прилад  . Попередньо були оцінені границі основної відносної похибки
. Попередньо були оцінені границі основної відносної похибки 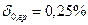 . Оціните границі відносної додаткової температурної похибки.
. Оціните границі відносної додаткової температурної похибки.
Розв’язання. 1. Визначаємо відхилення температури від нормальної області

2. Обчислюємо границі (відносної) додаткової температурної похибки
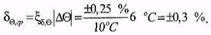
Задача 48.Коефіцієнт підсилення вимірювального підсилювача становить  . Діапазон вхідної напруги підсилювача становить
. Діапазон вхідної напруги підсилювача становить  , абсолютна похибка на вході підсилювача —
, абсолютна похибка на вході підсилювача — 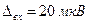 . Знайти абсолютну похибку на виході підсилювача.
. Знайти абсолютну похибку на виході підсилювача.
Розв’язання. Оскільки функція перетворення підсилювача є лінійною і проходить через початок координат

то згідно з (10.19) похибка на виході підсилювача становить
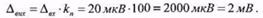
Задача 49.Напругу на виході подільника напруги 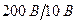 виміряли з похибкою 5 мВ. Визначити абсолютну похибку на вході подільника напруги
виміряли з похибкою 5 мВ. Визначити абсолютну похибку на вході подільника напруги
Розв’язання. Оскільки функція перетворення подільника напруги є лінійною і проходить через початок координат

де 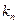 — коефіцієнт перетворення подільника — величина, обернена до коефіцієнта ділення
— коефіцієнт перетворення подільника — величина, обернена до коефіцієнта ділення 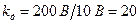

то згідно з (10.21) похибка на вході подільника напруги становить
 |
|
Задача 50.Для умови прикладу 10.10 знайти відносну похибку підсилювача, якщо вхідна напруга дорівнює діапазону  .
.
Розв’язання. Відносна похибка на вході підсилювача

Оскільки функція перетворення підсилювача є лінійною і проходить через початок координат, то відносні похибки на вході і виході підсилювача є однаковими, тобто
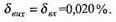
Задача 51.Для умови прикладу 10.11 знайти відносну похибку на вході подільника напруги, якщо виміряне значення вихідної напруги дорівнює діапазону  .
.
Розв’язання. Відносна похибка напруги на виході подільника

Оскільки функція перетворення подільника напруги є лінійною і проходить через початок координат, то відносні похибки на вході і виході подільника є однаковими, тобто
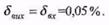
Задача 52.Функція перетворення мідного терморезиетивного перетворювача (залежність вихідного опору 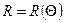 від температури (вхідної)
від температури (вхідної)  (у
(у 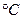 ) описується виразом
) описується виразом

де  — початковий опір при температурі
— початковий опір при температурі 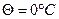 , (наприклад,
, (наприклад,  ),
), 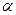 — коефіцієнт відносної чутливості - відносної зміни опору зі зміною температури (наприклад,
— коефіцієнт відносної чутливості - відносної зміни опору зі зміною температури (наприклад, 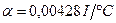 ).
).
Значення вихідного опору перетворювача  виміряли з похибкою, приблизне значення якої становить
виміряли з похибкою, приблизне значення якої становить  .
.
Оцінити абсолютну похибку вимірювання температури (звести похибку до входу перетворювача).
Розв’язання. Оскільки функція перетворення перетворювача є лінійною з крутістю (похідною)

то згідно з (10.17) зведена до входу абсолютна похибка

Задача 53.Для умови прикладу 10.14 знайти значення відносних похибок на виході та вході перетворювача і порівняти їх.
Розв’язання. Відносна похибка на виході перетворювача

Щоб визначити відносну похибку на вході, необхідно знайти значення вхідної величини-температури, яка відповідає виміряному значенню вихідної величини-опору.
Для цього необхідно скористатися виразом функції перетворення мідного терморезис-тивного перетворювача і знайти обернену функцію перетворення

Тоді відносна похибка на вході перетворювача

Отже, відносні похибки на вході та виході перетворювача є різними.
Задача 54.Функція перетворення платинового терморезистивного перетворювача (залежність вихідного опору 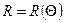 від температури (вхідної)
від температури (вхідної)  (у
(у 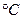 ) описується виразом
) описується виразом

де  — початковий опір при температурі
— початковий опір при температурі 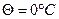 , (наприклад,
, (наприклад,  ),
), 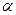 ,
,  — коефіцієнти залежності (наприклад,
— коефіцієнти залежності (наприклад,  ,
, 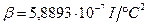 ).
).
Значення вихідного опору перетворювача 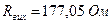 виміряли з похибкою, приблизне значення якої становить
виміряли з похибкою, приблизне значення якої становить 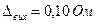 .
.
Оцінити абсолютну похибку вимірювання температури (звести похибку до входу перетворювача).
Розв’язання. Оскільки функція перетворення перетворювача є нелінійною (параболічного), то, щоб знайти значення крутості (похідної)
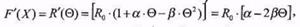
необхідно знати значення температури, якій відповідає виміряне значення опору, використовуючи, наприклад, так звану градуювальну таблицю, в якій наведено відповідності між вхідною та вихідною величинами перетворювача або аналітичний вираз оберненої функції перетворення перетворювача - залежність вхідної величини від вихідної. Для параболічної функції перетворення обернена функція має вигляд

Тоді, підставляючи коефіцієнти функції перетворення та виміряне значення опору, знайдемо значення температури

Далі розрахуємо значення крутості функції в точці 

Тоді за виразом (10.17) знаходимо зведене до входу значення абсолютної похибки
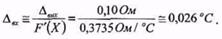
Задача 55.Для умови прикладу 10.16 знайти значення відносних похибок на виході та вході перетворювача і порівняти їх.
Розв’язання. Відносна похибка на виході перетворювача

Відносна похибка на вході перетворювача

Отже, тут також відносні похибки на вході та виході перетворювача є різними.