 |
|
Термодинамические потенциалы
Термодинамические потенциалы, определенные функции объема V, давления p, температуры T, энтропии S, числа частиц системы N и других макроскопических параметров x, характеризующих состояние термодинамической системы. К ним относятся:
внутренняя энергия U = U(S,V,N,x);
энтальпия H = H(S,p,N,x);
свободная энергия F = F(V,T,N,x);
энергия Гиббса G = G(p,T,N,x). (13.61)
Внутренняя энергия - энергия системы, зависящая от ее внутреннего состояния. Внутренняя энергия включает энергию хаотического (теплового) движения всех микрочастиц системы (молекул, атомов, ионов и т.д.) и энергию взаимодействия этих частиц. Кинетическая энергия движения системы как целого и ее потенциальная энергия во внешних силовых полях во внутреннюю энергию системы не входят.
В термодинамике представляет интерес не само значение внутренней энергии системы, а ее изменение при изменении состояния системы. Поэтому обычно принимают во внимание только те составляющие внутренней энергии, которые изменяются в рассматриваемых процессах изменения состояния системы.
Понятие "внутренняя энергия" ввел в 1851 г. У. Томсон, определив изменение внутренней энергии системы в каком-нибудь процессе как алгебраическую сумму количества теплоты Q, которыми система обменивается в ходе процесса с окружающей средой, и работы А, совершенной системой или произведенной над ней. Это отражает первое начало термодинамики
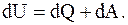13.62)
Принято считать работу положительной, если она производится системой над внешними телами, а количество теплоты положительным, если оно передается системе.
Внутренняя энергия является однозначной функцией состояния физической системы, т.е. однозначной функцией независимых переменных, определяющих это состояние, например температуры T и объема V (или давления p). Однозначность внутренней энергии приводит к тому, что, хотя, каждая из величин Q и A зависит от характера процесса, переводящего систему из состояния с внутренней энергией U в состояние с энергией U, изменение DU определяется лишь значениями внутренней энергии в начальном и конечном состояниях
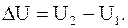(13.63)
Для любого замкнутого процесса, возвращающего систему в первоначальное состояние, изменение внутренней энергии равно нулю (U1 = U2; DU = 0; dQ = dA).
Изменение внутренней энергии системы в адиабатическом процессе (при dQ = 0) равно работе, производимой над системой или произведенной системой dU = dA.
В случае простейшей физической системы с малым межмолекулярным взаимодействием - идеального газа - изменение внутренней энергии сводится к изменению кинетической энергии молекул:
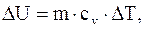(13.64)
где m - масса газа;
cv - удельная теплоемкость при постоянном объеме;
DT – изменение температуры системы.
Поэтому DU для идеального газа определяется только изменением температуры DT (закон Джоуля). В физических системах, частицы которых взаимодействуют между собой (реальные газы, жидкости, твердые тела), внутренняя энергия включает также энергию межмолекулярного и внутримолекулярного взаимодействий. Внутренняя энергия таких систем зависит как от температуры, так и от давления (объема).
Экспериментально может быть измерено только изменение внутренней энергии в каком-либо физическом процессе, то есть внутренняя энергия определяется с точностью до постоянного слагаемого.
Методы статистической физики позволяют в принципе теоретически рассчитать внутреннюю энергию физической системы, но также лишь с точностью до постоянного слагаемого, зависящего от выбранного нуля отсчета.
В области низких температур при T®0 внутренняя энергия конденсированных систем (жидких и твердых тел) приближается к определенному постоянному значению U, которое может быть принято за начало отсчета внутренней энергии.
Дифференцированием U по S и V можно определить ряд других параметров системы.
Энтальпия (теплосодержание, тепловая функция Гиббса) - характеризует состояние макроскопической системы в термодинамическом равновесии при выборе в качестве основных независимых переменных энтропии S и давления p - H(S,p,N,x).
Энтальпия аддитивная функция (т.е. энтальпия всей системы равна сумме энтальпий составляющих ее частей). С внутренней энергией U системы энтальпия связана соотношением
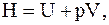(13.65)
где V - объем системы.
Полный дифференциал энтальпии (при неизменных N и x) имеет вид
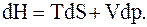(13.66)
Из формулы (13.66) можно определить температуру T и объем V системы
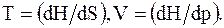(13.67)
При постоянном давлении теплоемкость системы
Cp = (dH/dt). (13.68)
Эти свойства энтальпии при постоянном давлении аналогичны свойствам внутренней энергии при постоянном объеме
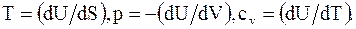(13.69)
Равновесному состоянию системы при постоянных значениях энтропии S и давлении p соответствует минимальное значение энтальпии. Изменение энтальпии (DH) равно количеству теплоты, которое сообщают системе или отводят от нее при постоянном давлении, поэтому значения H характеризуют тепловые эффекты фазовых переходов (плавления, кипения и т. д.), химических реакций и других процессов, протекающих при постоянном давлении. При тепловой изоляции тел (и постоянном давлении p) энтальпия сохраняется, поэтому ее иногда называют теплосодержанием или тепловой функцией. Условие сохранения энтальпии лежит, в частности, в основе теории эффекта Джоуля - Томсона, нашедшего важное практическое применение при сжижении газов. Термин "энтальпия" был предложен Х. Камерлинг-Оннесом.
Свободная энергия - одно из названий изохорно-изотермического термодинамического потенциала или Гельмгольца энергии. Она определяется как разность между внутренней энергии термодинамической системы (U) и произведением ее энтропии (S) на температуру (T)
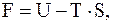(13.70)
где T×S - связанная энергия.
Энергия Гиббса это изобарно-изотермический потенциал. Свободная энтальпия, характеристическая функция термодинамической системы при независимых параметрах p, T и N (G). Она определяется через энтальпию H, энтропию S и температуру T равенством
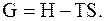(13.71)
Со свободной энергией (энергией Гельмгольца), энергия Гиббса связана соотношением
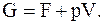(13.72)
Энергия Гиббса пропорциональна числу частиц N; отнесенная к одной частице, она называется химическим потенциалом. Гиббса энергия удобна для описания процессов, в которых возможен обмен веществом с окружающими телами. Понятие "Гиббса энергия" введено в термодинамику Дж. У. Гиббсом. В изотермически равновесном процессе, при постоянном давлении, убыль Гиббса энергии системы равна полной работе системы за вычетом работы против внешнего давления, (т.е. равна полезной максимальной работе). Ее обычно выражают в кДж/кг или кДж/моль.
Зная термодинамические потенциалы как функции выше указанных параметров, их дифференцированием можно получить все остальные параметры, характеризующие систему, подобно тому, как в механике можно определить компоненты действующих на систему сил, дифференцируя потенциальную энергию системы по соответствующим координатам.
Если известен какой-либо термодинамический потенциал, то можно определить все термодинамические свойства системы, в частности получить уравнение состояния системы. Термодинамические потенциалы выражают условия термодинамического равновесия системы и критерии его устойчивости.
Совершаемая термодинамической системой в каком-либо процессе работа определяется убылью термодинамического потенциала, отвечающего условиям процесса.
Так, например:
а) при постоянстве числа частиц (N = const) в условиях теплоизоляции (адиабатический процесс, S = const) элементарная работа dA равна убыли внутренней энергии
;
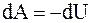б) при изотермическом процессе (T = const)
.
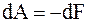В этом процессе работа совершается не только за счет внутренней энергии, но и за счет поступающей в систему теплоты;
в) для систем, в которых возможен обмен веществом с окружающей средой (изменение N), возможны процессы при постоянном давлении p и постоянной температуре T. В этом случае элементарная работа dA всех термодинамических сил кроме сил давления, равна убыли термодинамического потенциала Гиббса (G), т.е.
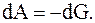
Теоретическое определение термодинамических потенциалов как функций соответствующих переменных составляет основную задачу статистической термодинамики. Термодинамические потенциалы широко применяются для получения общих соотношений между физическими свойствами макроскопических тел и анализа термодинамических процессов и условий равновесия в физико-химических системах.
13.6. Третье начало термодинамики. Применения термодинамики
Согласно второму началу термодинамики, энтропия определяется с точностью до постоянного слагаемого, которое хотя и не зависит от температуры, но могло бы быть различным для разных тел в состоянии равновесия.
Соответствующие неопределенные слагаемые существуют и в термодинамических потенциалах. Немецкий физик В. Нернст (1906) на основе физико-химических исследований пришел к выводу, что эти слагаемые универсальны: они не зависят от давления, агрегатного состояния и других характеристик вещества. Этот новый, вытекающий из опыта принцип обычно называют третьим началом термодинамики или тепловой теоремой Нернста.
Согласно теореме Нернста изменение энтропии (DS) при любых обратимых изотермических процессах, совершаемых между двумя равновесными состояниями при температурах, приближающихся к абсолютному нулю, стремится к нулю
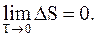(13.73)
Другая эквивалентная формулировка теоремы Нернста: "При помощи последовательности термодинамических процессов нельзя достичь температуры, равной абсолютному нулю".
Теорема Нернста приводит к ряду важных термодинамических следствий.
М. Планк (1911) показал, что третье начало термодинамики равносильно условию: энтропия всех тел в состоянии равновесия стремиться к нулю по мере приближения температуры к абсолютному нулю (поскольку универсальную константу в выражении энтропии можно положить равной нулю).
Из третьего начала термодинамики следует, в частности, что коэффициент теплового расширения, изохорный коэффициент давления (dp/dT) и удельные теплоемкости cp и cv обращаются в нуль при T®0.
Необходимо отметить, что третье начало термодинамики и вытекающие из него следствия не относятся к системам, находящимся в так называемом заторможенном состоянии. Примером такой системы является смесь веществ, между которыми хотя и возможны химические реакции, но они заторможены - скорость реакций при низких температурах очень мала.
Другим примером может служить быстро замороженный раствор, который при низкой температуре должен был бы расслоиться на две фазы, но процесс расслоения при низких температурах практически не происходит. Такие состояния во многих отношениях подобны равновесным состоянием, однако, их энтропия не обращается в нуль при абсолютной температуре стремящейся к нулю.
Термодинамика не опирается на модельные представления об атомной структуре вещества и может применяться для исследования всех систем, для которых справедливы законы, лежащие в ее основе.
Методами термодинамики устанавливаются связи между непосредственно наблюдаемыми (макроскопическими) характеристиками систем (их давлением, объемом, температурой и др.) в различных термодинамических процессах.
Важными областями применения термодинамики являются также теория химического равновесия и теория фазового равновесия, в частности равновесия между различными агрегатными состояниями и равновесия при расслоении на фазы смесей жидкостей и газов. В этих случаях в процессе установления равновесия существенную роль играет обмен частицами вещества между разными фазами, и при формулировке условий равновесия используется понятие химического потенциала, постоянство которого заменяет условие постоянства давления, если жидкость или газ находятся во внешнем поле, например в поле тяготения.
В термодинамике принято выделять разделы: а) относящиеся к отдельным наукам и к технике, например, химическая термодинамика, техническая термодинамика и другие; б) к различным объектам исследования, например, термодинамика газов, термодинамика диэлектриков, термодинамика излучения.
Лекция 14. Элементы неравновесной термодинамики
Термодинамика неравновесных процессов. Закон сохранения массы в термодинамике неравновесных процессов. Закон сохранения импульса в термодинамике неравновесных процессов. Закон сохранения энергии в термодинамике неравновесных процессов. Уравнение баланса энтропии.