Главная | Обратная связь

Изотермический процесс

Изотермический процесс. Это процесс, протекающий при постоянной температуре (T = const). Тогда

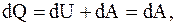(13.3)

т.к. dU = C_v×dT = 0, то U = const, т.е. все подводимое к системе тепло идет на совершение этой системой работы, которую можно рассчитать так

, а . (13.4)

Из уравнения состояния идеального газа для моля или киломоля идеального газа , следовательно,

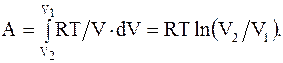
(13.5)

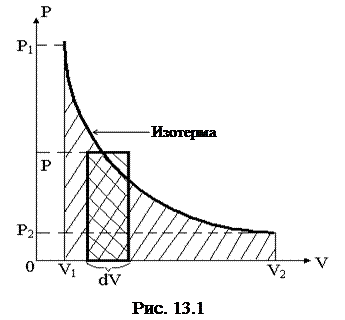
Графически эту работу (в координатах p, V) можно представить в виде площади фигуры, ограниченной изотермой ab, осью OV и прямыми V₁ и V₂ (рис.13.1).

Из полученного результата можно сделать вывод: при изотермическом процессе работа, совершаемая системой, зависит только от соотношения начального и конечного объемов.

13.1.1.2. Изобарический процесс

Изобарический процесс. Это процесс, протекающий при постоянном давлении (p = const).

В этом случае

(13.6)

т.е. подводимое к системе тепло идет как на изменение ее внутренней энергии, так и на совершение этой системой работы. При этом

(13.7)

Определим долю подводимой к системе энергии, которая идет на совершение работы, и долю этой энергии, которая идет на изменение внутренней энергии системы. Известно, что

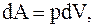(13.8)

но для моля или киломоля идеального газа следовательно, 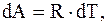тогда

. (13.9)

Изменение внутренней энергии

(13.10)

где g = C_p/C_v.

13.1.1.3. Изохорический процесс

Изохорический процесс. Это процесс, протекающий при постоянном объеме (V = const).

Первое начало термодинамики

, (13.11)

так как, . Таким образом, при изохорическом процессе, все подводимое к системе тепло идет на изменение ее внутренней энергии. При этом

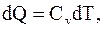(13.12)

следовательно

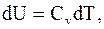
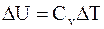. (13.14)

Изменение внутренней энергии системы пропорционально изменению ее температуры.

13.1.1.4. Адиабатический процесс

Очень часто на практике приходится иметь дело с процессами, протекающими без теплообмена или почти без теплообмена с окружающей средой. Такие процессы называют адиабатическими или адиабатными. Примером адиабатического процесса может служить быстро протекающий процесс сжатия или расширения газа.

Найдем зависимость между давлением и объемом при адиабатическом процессе, для чего воспользуемся первым началом термодинамики 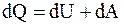, так как , то

, а , (13.15)

т.е. работа, совершаемая системой при адиабатическом процессе, сопровождается изменением ее внутренней энергии. Но, а dU = C_v×dT, тогда

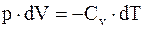. (13.16)

Из уравнения состояния идеального газа для моля или киломоля , следовательно

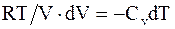или 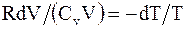откуда, т.е. , а

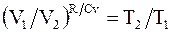. (13.17)

Известно, что , а , тогда

;

или

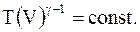(13.18)

Следовательно, при адиабатических процессах произведение температуры на объем в степени (g - 1 ) для данной массы остается величиной постоянной.

Из полученного видно, что при адиабатическом расширении идеального газа его температура уменьшается, а при адиабатическом сжатии - увеличивается.

Из уравнения Менделеева - Клапейрона для моля или киломоля идеального газа 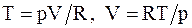. Подставляя значения T и V в уравнение (13.18), имеем

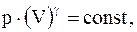
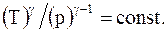(13.19)

Уравнения (13.18 и 13.19), связывающие давление и объем, температуру и объем, температуру и давление при адиабатическом процессе называют уравнениями Пуассона.

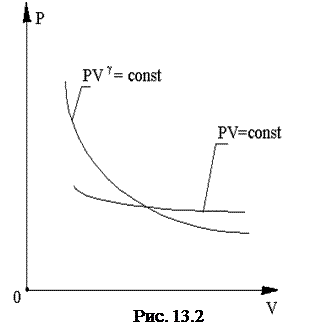
Графически (в координатах p, V) адиабатический процесс можно представить адиабатой. При этом адиабата располагается более круто, чем изотерма (рис. 13.2). Это объясняется тем, что при изотермическом сжатии давление возрастает за счет изменения молекулярной плотности, т.е. за счет увеличения числа ударов молекул о стенки сосуда. При адиабатическом процессе сжатие сопровождается повышением температуры, т.е. давление возрастает не только за счет увеличения молекулярной плотности, но и за счет роста средней скорости движения молекул.

Следует иметь в виду, что каждая точка адиабаты имеет температуру, отличную от других, следовательно, через каждую точку адиабаты можно провести соответствующую изотерму и наоборот.

Определим работу, совершаемую идеальным газом при адиабатическом расширении. В этом случае работа совершается за счет изменения (уменьшения) его внутренней энергии:

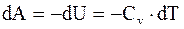, а (13.20)

откуда

(13.21)

но, следовательно

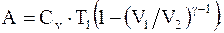(13.22)

Так как , то

или 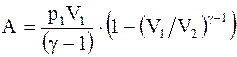. (13.23)

Графически эта работа изображается площадью фигуры, ограниченной адиабатой, осью OV, и прямыми V₁ и V₂ (рис.13.3).

Надо отметить, что все рассмотренные процессы в идеальных газах являются частными случаями политропического процесса.

Политропическим процессом называют такой, при котором p и V связаны соотношением

, (13.24)

где n - показатель политропы, принимающий любые значения от - ¥ до + ¥. В частности для изобарического процесса n = 0; изотермического n = 1; адиабатического n = g; изохорического n = ¥.

Можно показать, что работа, совершаемая идеальным газом при политропическом процессе, определяется соотношением

(13.25)

Теплоемкость тела при адиабатном процессе 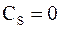, т.к. . Это означает, что теплоемкость при различных термодинамических процессах может принимать любые значения от -¥ до +¥. Указанное обстоятельство можно проиллюстрировать при помощи так называемой шкалы теплоемкостей:

Отметим, что к числу адиабатных процессов, относится процесс распространения звука (ультразвука) в газообразной и жидкой средах. Это связано с тем, что при быстропеременных процессах теплообмен между соседними участками с различной температурой (между соседними полуволнами) не успевает произойти.

13.2. Обратимые, необратимые и круговые процессы (циклы)

Обратимым называется такой процесс, который протекает так, что после его окончания систему можно вернуть в первоначальное состояние, причем никаких изменений в окружающей систему среде не произойдет.

Средой называются все не входящие в систему тела, с которыми она взаимодействует.

Примером обратимого процесса может служить колебательное движение математического маятника в отсутствии сил трения и сопротивления. Так в действительности практически все процессы сопровождаются силами трения, сопротивления или теплопередачей, то понятие обратимого процесса является научной абстракцией.

Процесс, протекающий так, что после его окончания систему нельзя вернуть в первоначальное состояние без изменений в окружающей среде, называется необратимым.

Примером необратимых процессов могут служить все процессы, которые сопровождаются силами трения, сопротивления или теплопередачей. Например, процесс передачи тепла всегда происходит от более нагретого тела к менее нагретому телу, или более нагретой части какого - либо тела к менее нагретой части этого же тела. Обратный процесс невозможен. В природе все процессы необратимы.

Кроме обратимых и необратимых процессов в термодинамике большое значение имеют различные круговые процессы или циклы.

Круговым процессом (циклом) называется такая последовательность превращений, в результате которой система, выйдя из какого-либо исходного состояния, возвращается в него вновь (рис.13.4).

Любой круговой процесс состоит из процессов расширения и сжатия. Процесс расширения сопровождается работой, совершаемой системой, а процесс сжатия - работой, совершаемой над системой внешними силами. Разность этих работ равна работе данного цикла.

Из первого начала термодинамики видно, что работа при расширении может совершаться либо за счет подводимого к системе тепла, либо за счет уменьшения ее внутренней энергии. Работа при сжатии сопровождается либо отводом от системы некоторого количества тепла, либо увеличением ее внутренней энергии.

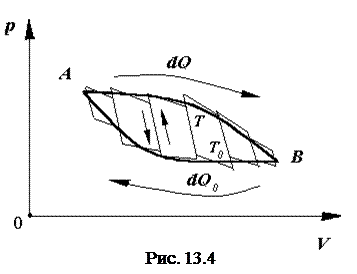Если работа при расширении больше, чем работа при сжатии, то такой процесс (цикл) называется прямым. В противном случае – цикл обратный.

Рассмотрим один из возможных круговых процессов (рис.13.5).

Пусть некоторая система, например, один моль идеального газа из состояния с параметрами p₁, V₁, T₁ перешла изотермически в состояние с параметрами p₂, V₂, T₁. При этом системой за счет подвода некоторого количества тепла Q₁ при температуре Т₁, была совершена работа

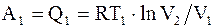. (13.26)

Для перехода системы в состояние с параметрами p₃, V₃, T₂ (при V₂ = const) надо понизить ее температуру от T₁ до T₂ ,что возможно, если система отдаст некоторое количество теплоты

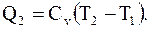(13.27)

Изотермический переход системы в состояние с параметрами p₄, V₄, T₂ можно осуществить, совершая над ней работу, что возможно, только при отводе от нее эквивалентного количества тепла Q₃ = A₂.

.(13.28)

Для завершения цикла систему необходимо нагреть до температуры T₁, подводя к ней некоторое количество тепла

. (13.29)

Так как Q₂ = Q₄, то работа цикла равна и эквивалентна разности количеств тепла, подводимого к системе при расширении и отводимого от нее при сжатии

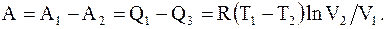(13.30)

Для характеристики эффективности цикла вводится в рассмотрение физическая величина, называемая коэффициентом полезного действия, равная отношению работы цикла к работе, которую можно было бы совершить при превращении в нее всего количества тепла, подведенного к системе

(13.31)

Превращение теплоты в работу используется в тепловых машинах. При этом более совершенной считается такая тепловая машина, у которой КПД стремится к единице.

13.3. Цикл Карно. Максимальный КПД тепловой машины

Наиболее совершенным в отношении КПД является цикл Карно, который состоит из двух изотерм (1-2, 3-4) и двух адиабат (2-3, 4-1) (рис.13.6).

Пусть один моль или киломоль идеального газа в состоянии 1 имеет параметры p₁, V₁, T₁.

После изотермического перехода из состояния 1 в состояние 2, его параметры изменяются p₂, V₂, T₁, при этом он совершает работу, которая численно будет равна количеству тепла, подводимому к системе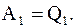

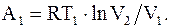(13.32)

При адиабатическом расширении из состояния 2 в состояние 3 газ, совершив работу за счет изменения внутренней энергии, приобретет параметры p₃, V₃, T₂. При этом

(13.33)

Для возвращения системы в первоначальное состояние необходимо газ изотермически сжать при температуре T₂ до объема V₄. А это возможно только в том случае, если от системы отбирается некоторое количество тепла Q₂, равное работе над системой

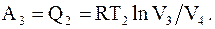(13.34)

При этом параметры газа станут равными p₄, V₄, T₂. Затем сжать адиабатически из состояния 4 в состояние 1. В этом случае, за счет работы, совершаемой над газом, произойдет увеличение внутренней энергии газа на величину

(13.35)

Разность между работой, совершенной системой при расширении, и работой, совершенной над системой при ее сжатии, будет равна работе цикла Карно

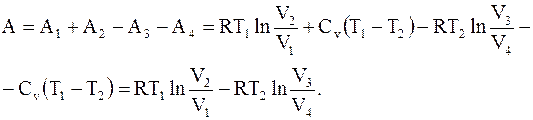(13.36)

Тогда h цикла Карно

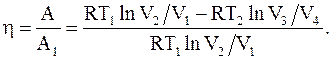(13.37)

Объемы V₂ и V₃, V₁ и V₄ лежат на соответствующих адиабатах, следовательно, согласно уравнениям Пуассона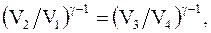

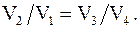
Таким образом

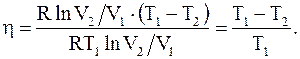(13.38)

Из полученного соотношения видно, что h цикла Карно не зависит от природы вещества, а зависит лишь от температур, при которых теплота, сообщается системе и отбирается от нее.

Коэффициент полезного действия цикла Карно стремится к единице при возрастании T₁ и стремлении к нулю температуры T₂.

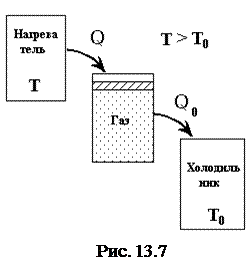
За цикл Карно часть тепла отбирается от внешнего по отношению к системе тела - нагревателя и передается системе. Часть ее превращается в работу, часть - отдается холодильнику. Такой цикл Карно встречается в тепловых машинах (рис. 13.7).

Надо иметь в виду, что цикл Карно обратим, что используется в холодильных машинах. В этом случае в результате совершения работы удается перевести некоторое количество теплоты от тела более холодного к телу более нагретому. Коэффициент полезного действия холодильной машины (холодильника)

(13.39)

Кроме цикла Карно в технической термодинамике применяются цикл Отто, состоящий из двух адиабат и двух изохор, и цикл Дизеля, состоящий из двух адиабат, изохоры и изобары (рис.13.8).