Главная | Обратная связь

Реальные газы. Молекулярные силы. Уравнение Ван-дер-Ваальса. Изотермы Ван-дер-Ваальса и экспериментальны изотермы реальных газов

Как известно атомы содержат положительно заряженные ядра и электронную оболочку (электронное облако). Размеры ядер очень малы ~10^-15 - 10^-14м. Радиус орбиты электрона составляет порядка ~10^-10 м=1 . При сближении молекул до расстояния около двух - трех диаметров (3 ) начинают проявляться взаимодействие зарядов ядер и электронных оболочек.

Прежде всего, при сближении начинают проявляться силы притяжения F<0 (рис. 15.1).

Однако когда молекулы подойдут "вплотную" друг к другу и "соприкасаются" своими оболочками, то дальнейшее их сближение затрудняется. Между электронными оболочками возникнут огромные силы отталкивания, резко возрастающие по мере дальнейшего проникновения оболочек друг в друга. Начинают преобладать силы отталкивания F>0. На нижнем графике дана зависимость потенциальной энергии взаимодействия молекул от расстояния между их центрами U(r). Когда результирующая сила межмолекулярного взаимодействия равна нулю (при r=r₀) потенциальная энергия минимальна, W_{p min}<0, т.е. для удаления молекул друг от друга необходимо, чтобы внешние силы, совершили работу.

Между тремя основными агрегатными состояниями имеется значительное расхождение в величине энергии межмолекулярного взаимодействия. Так, например, для:

1) газов кТ>>W_{p min};

2) кристаллических твердых тел кТ<<W_{p min};

3) жидкостей кТ»W_{p min}.

Движение молекул и структура вещества существенно зависят от соотношения энергии теплового движения и потенциальной энергии взаимодействия между молекулами.

Если моль газа находится при нормальных условиях (p@10⁵, T»300К), то молекулы настолько удалены друг от друга, что их взаимодействием можно пренебречь, можно пренебречь также и их линейными размерами. Поэтому для этих условий хорошо выполняется уравнение состояния идеального газа, уравнение Менделеева - Клапейрона

. (15.1)

Однако при высоких давлениях и низких температурах молекулы настолько сближаются, что уже нельзя пренебречь их взаимодействием и их собственными размерами. Поэтому в уравнение (15.1) необходимо ввести поправки на "собственный" объем молекул и дополнительное внутреннее давление, которое обусловлено взаимодействием молекул.

Поправку на собственный объем молекул можно ввести из следующих соображений. Очевидно, молекула не может находиться в тех местах, где размещены остальные N-1 молекула. Для каждой пары взаимодействующих молекул недоступной является та часть объема, в которой расстояние между их центрами равно d, т.е. сфера радиуса d (рис. 15.2), объем которой составляет (4/3)pd³, для всех молекул недоступным является объем .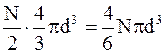

Сомножитель 1/2 появился вследствие того, что при парном взаимодействии недоступным считается объем, образованный половиной (N/2) молекул. Итак, поправка на недоступный ("собственный") объем составляет , т.е. недоступный объем равен учетверенному объему всех молекул газа в сосуде. Таким образом, поправка на собственный объем молекул , где 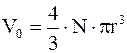- суммарный собственный объем молекул газа, уравнение состояния реального газа можно записать так (для моля или киломоля)

. (15.2)

Силы межмолекулярного взаимодействия, силы притяжения, проявляются при условии достаточного сближения молекул. Следовательно, в уравнение состояния реального газа необходимо ввести о так называемую поправку "на внутреннее давление", которое обуславливают силы межмолекулярного взаимодействия. Поправка на "внутреннее давление" в уравнении состояния реального газа, вводится из следующих соображений. Пусть молекулы окружают воображаемую плоскую пластинку, как это показано на рис.15.3. Естественно считать, что f₁ - сила, действующая на данную молекулу со стороны молекул, находящихся справа от пластины f₁~n. Где n -концентрация молекул справа от стенки. Тогда дополнительное давление со стороны молекул слева от пластины будет пропорционально концентрации молекул слева от нее, т.е. Поэтому, дополнительное давление . С учетом сказанного можно записать , где "а" зависит от конкретного вида молекул, т.е. газа.

Ударяющиеся о стенку сосуда, в котором находится газ, молекулы, притягиваются остальными молекулами, следовательно, давление газа на стенки сосуда уменьшается на некоторую среднюю величину p' (давление p' иногда называют внутренним давлением).

Вводя в уравнение (15.2) поправку на внутреннее давление, будем иметь

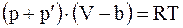; ; . (15.3)

Уравнение (15.3) - уравнение состояния моля или киломоля реального газа, уравнение Ван-дер-Ваальса.

Для произвольной массы газа его можно записать в следующем виде

. (15.4)

Это уравнение представляет собой уравнение 3^ей степени относительно объема V

. (15.5)

Следовательно, при данных значениях p и Т, известных значениях a и b оно имеет три решения (V₁<V₂<V₃). При этом корни уравнения либо все три вещественные, либо один вещественный и два мнимых (комплексно сопряженных), не имеющих физического смысла.

Задавая различные значения p, решая уравнение Ван-дер-Ваальса для нескольких избранных, но постоянных значений температуры газа T, можно построить семейство изотерм Ван-дер-Ваальса, представленных на рис.15.4.

При высоких температурах (T>T_k) поправка мало по сравнению с p и этой поправкой можно пренебречь. К тому же если собственный объем молекул мал по сравнению с объемом, занимаемым газом (b<<V), то уравнение Ван-дер-Ваальса имеет один вещественный корень и переходит в уравнение Менделеева.-Клапейрона, справедливое для идеальных газов. При высоких температурах изотермы Ван-дер-Ваальса имеют вид изотерм pV = const и характеризуют газообразное состояние вещества.

При уменьшении температуры форма изотерм изменяется и при некотором значении T = T_к, изотермы имеют точку перегиба "К".

В области T<T_k имеется интервал давлений, в котором уравнение (15.3) имеет три вещественных корня. Наибольший корень V₃ соответствует наименьшей плотности вещества и относится к газовому состоянию. Наименьший корень V₁ к наиболее плотному бесструктурному состоянию, т.е. к жидкости. Средний корень V₂, приходящийся на восходящую ветвь изотермы, соответствует неустойчивому, а поэтому практически ненаблюдаемому состоянию. Действительно, любое флуктуационное изменение объема V₂ влечет за собой такое изменение давления газа, при котором точка изотермы, характеризующая его состояние, неизбежно переходит с восходящей ветви кривой на нисходящую ветвь. В точке K на изотерме T_k все три корня уравнения Ван-дер-Ваальса вещественны и равны (V₁=V₂=V₃=V_k). Такое состояние газа называется критическим и, ему соответствуют определенные значения p_k, V_k, T_k. Так как, согласно теореме Безу (V – V_k)³ = 0, то из сравнения коэффициентов при соответствующих степенях в (15.5) получим

(15.6)

Откуда

или 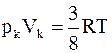. (15.7)

Таким образом, по экспериментально найденным значениям V_k и T_k, для данной массы вещества, из системы уравнений (15.7) можно определить параметры газа "a" и "b" и значение p_k. По известным "a", "b" и R – критические параметры газа (p_k, T_k и соответствующий массе газа объем V_k).

В табл. 15.1 приведены значения p_k и T_k для некоторых жидкостей. Как видно, критическая температура приблизительно в 1,5 раза превышает температуру кипения жидкости при нормальном внешнем давлении.