Главная | Обратная связь

Энтропия системы и её свойства. Определение изменения энтропии системы, совершающей какой-либо изопроцесс

Известно, что внутренняя энергия системы является функцией ее состояния. Характеристикой различных термодинамических процессов является энтропия. Энтропия системы физическая величина, элементарное изменение которой при переходе системы из одного состояния в другое равно полученному или отданному количеству теплоты, деленному на температуру, при которой произошел этот процесс. Энтропия, подобно внутренней энергии, является однозначной функцией состояния системы.

Бесконечно малое изменение энтропии определяется соотношением

(13.40)

При переходе системы из одного состояния в другое, изменение энтропии можно рассчитать так

(13.41)

На основании первого начала термодинамики

тогда

а

(13.42)

Зная общую формулу для расчета изменения энтропии можно рассчитать изменение энтропии, если система совершает какой-либо изопроцесс, например:

1. Изотермический.

Известно, что при изотермическом процессе T = const, т.е. T₁=T₂, тогда

(13.43)

2. Изобарический.

Известно, что при изобарическом процессе p = const, т.е. V₂/V₁ = T₂/T₁, следовательно

(13.44)

3. Изохорический.

При изохорическом процессе V = const, т.е. V₂ = V₁. Таким образом,

(13.45)

4. Адиабатический.

Известно, что при адиабатическом процессе dQ = 0, т.е. DS = 0, следовательно

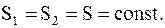(13.46)

Для любых изопроцессов энтропия системы равна сумме энтропии всех тел, входящих в нее.

Найдем выражение для изменения энтропии системы, совершающей цикл Карно. В этом случае

(13.47)

где DS_р - изменение энтропии рабочего тела;

DS_н, DS_х - изменение энтропии нагревателя и холодильника;

DS_пр - изменение энтропии "потребителя работы".

Так как рабочее тело при совершении цикла Карно возвращается в исходное состояние, то DS_р = 0; DS_п = 0 - энергия "потребителя работы" сообщается ему только в виде работы; DS_н = - Q₁/T₁; DS_х = - Q₂/T₂, что характерно для изотермических процессов. Таким образом

(13.48)

В случае совершения системой обратимого цикла Карно |Q₁|=|Q₂|, но Q₁>0, Q₂<0, следовательно, DS_обр = 0 или S_обр=const, т.е. энтропия замкнутой системы, совершающей обратимый цикл Карно не изменяется.

Если системой совершается необратимый цикл, то или откуда 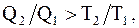следовательно т.е.

(13.49)

Таким образом, энтропия замкнутой системы, совершающей необратимый цикл, возрастает.

Объединяя полученные результаты для обратимых и необратимых процессов, для произвольных процессов, происходящих в замкнутой системе, будем иметь

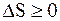(13.50)

т.е. энтропия замкнутой (изолированной) системы при любых, происходящих в ней процессах, не может убывать.

Для бесконечно малого изменения состояния системы, с учетом того, что энтропия замкнутой системы при любых процессах, происходящих в ней, не может убывать, можно сделать вывод, что

или (13.51)

где знак равенства справедлив для обратимых процессов, а знак неравенства - для необратимых.

Так, например, пусть необратимость процесса обусловлена только теплообменом при конечной разности между температурами нагревателя T и тела (T - DТ), тогда

(13.52)

Для обратимых процессов

. (13.53)

Определим работу для обратимых и необратимых изотермических процессов, воспользовавшись первым началом термодинамики в виде .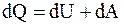

Так как из (13.51) 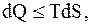то

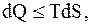(13.54)

Из выражения (13.54) для обратимого процесса можно получить

(13.55)

При изотермических процессах T = const, dT = 0, a

(13.56)

Таким образом, при обратимом изотермическом процессе работа, совершаемая системой над внешними телами, оказывается равной убыли некоторой величины F = U - T×S , которая называется свободной энергией. Она представляет собой ту часть внутренней энергии системы, которая превращается во внешнюю работу при обратимых изотермических процессах. Свободная энергия является функцией состояния системы.

Если процесс изотермический и необратимый, то т.е.

(13.57)

Таким образом, убыль свободной энергии определяет наибольшую величину работы, которую может совершить система при изотермическом процессе.

Величину T×S = U - F называют связанной энергией.

Связанная энергия представляет собой ту часть внутренней энергии, которая не может быть передана в виде работы при изотермическом процессе.