Главная | Обратная связь

Законы идеального газа

 

Состояние некоторой массы газа определяется заданием трех термодинамических параметров – давления р, объёма V и температуры Т. Связь между этими параметрами в общем виде можно выразить формулой F(p, V, T) = 0. Такое соотношение называется уравнением состояния системы (газа).

Простейшими свойствами обладает идеальный газ, т.е. газ, взаимодействием между молекулами которого можно пренебречь. Всякий достаточно разреженный газ близок к идеальному. Воздух, азот, кислород при обычных условиях (1 атм, комнатные температуры) мало отличаются от идеального газа.

Уравнение состояния идеального газа может быть записано в виде объединённого газового закона:

. (3)

Закон Авогадро: одинаковое количество молей любого газа при одинаковых температуре и давлении занимают одинаковые объёмы. В частности, при нормальных условиях: Т₀ = 273,15 K,
р₀ = 1 атм = 760 мм рт. ст. = 101325 Паобъём 1 моля равен V_М = 22,4 л. Отсюда следует, что, если любого газа взять 1 моль, то величина константы в уравнении (3) будет одинакова для всех газов. Обозначим её буквой R и назовем универсальной газовой постоянной:

.

Перепишем последнее уравнение в виде pV_M = RT.

Умножим его на произвольное число молей n: pV_Mn = nRT.

Учтем, что V_M n = V и n = m/M (где m – масса газа, а М – молярная масса), и получим уравнение Менделеева-Клапейрона (уравнение состояния для произвольной массы газа):

. (4)

Умножим и разделим правую часть уравнения Менделеева- Клапейрона (4) на число Авогадро N_А:

.

Произведение nN_A равно общему числу молекул N, а отношение R/N_A является постоянной Больцмана k. Итак, имеем:

pV= NkT, или , (5)

где n – концентрация частиц.

Изопроцессами называются термодинамические процессы, происходящие в системе при постоянной массе и каком-либо одном постоянном параметре состояния – p, V или T.

Пусть р₀ и V₀ – это давление и объём газа при 0 °С.

Изотермическийпроцесс (закон Бойля-Мариотта):

Т = const, pV = const.

Изобарный процесс (закон Гей-Люссака):

p = const, V/T = const или V = V₀ (1 + at),

где a = 1/273,15 K^-1 – коэффициент объёмного расширения. Если вместо температуры по шкале Цельсия t в последнее уравнение подставить температуру по шкале Кельвина(t = T - 273,15), то можно получить формулу V = V₀ aT.

Изохорный процесс (закон Шарля, 2-й закон Гей-Люссака):

V = const, p/T = const или p = p₀ (1 + at),

где a = 1/273,15 K^-1 – термический коэффициент давления. Если в это уравнение вместо температуры по шкале Цельсия t подставить температуру по шкале Кельвина (t = T - 273,15), то после преобразований получим p = p₀ aT.

Графики изопроцессов представлены на рис. 2.

 

 

Предположим, что в сосуде находится в тепловом равновесии смесь газов, химически не реагирующих между собой. Пусть N – общее число молекул в сосуде, а N₁, N₂ … – количества молекул компонент смеси. Найдем давление этой смеси:

= n₁ k T + n₂ k T + … = 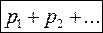, (6)

где p₁,р₂ … – парциáльные давления компонент смеси. Формула (6) показывает, что каждая группа молекул оказывает давление, не зависящее от других молекул. Поэтому можно сформулировать закон Дальтона: давление смеси химически не взаимодействующих газов равно сумме парциальных давлений.

Найдем молярную массу смеси.

Масса смеси равна m_С = m₁ + m₂ +…

Число частиц в смеси равно N_C = N₁ + N₂ + …

Найдем число частиц N, используя формулу N = N_An:

Отсюда находим молярную массу смеси:

. (7)