Главная | Обратная связь

Распределение Максвелла

 

Пусть имеется N молекул, находящихся в тепловом движении. Их скорости хаотически меняют величину и направление. Мáксвелл показал, что, несмотря на хаотичность, существует строго определенное и однозначное распределение скоростей между молекулами.

Отложим на оси скорости все возможные скорости молекул (рис. 9). Найдем количество молекул DN, скорости которых заключены в интервале [υ, υ + Dυ]. Очевидно, это количество DN будет пропорционально общему числу молекул N, размеру интервала скорости Dυ и функции распределения молекул по скоростям F(υ):

, или , или .

Физический смысл F(υ): при Dυ = 1 функция F(υ) = DN/N - доля частиц от общего числа, скорости которых заключены в единичном интервале вблизи скорости υ.

Условие нормировки: , т.е. число частиц, имеющих скорости в интервале [0, ¥], равно N (а N/N = 1).

Одна из форм записи функции распределения Максвелла имеет вид

, (19)

где υ – скорость на длине свободного пробега; m – масса одной молекулы; k – постоянная Больцмана; Т – температура.

График функции F(υ) показан на рис. 10. Как и следовало ожидать, F(υ) = 0 при υ = 0 и υ = ¥, т.е. в газе нет неподвижных молекул и движущихся с бесконечно большими скоростями.

Найдем наиболее вероятную скорость υ_ВЕР, определяющую максимум кривой распределения. Для этого следует взять производную и приравнять её к нулю (постоянные множители при этом вынесутся за знак производной):

,

,

.

Корнями последнего уравнения будут

, , .

Первые два корня – это минимумы функции F(υ), а третий корень – максимум (наиболее вероятная скорость):

. (20)

 

Найдем значение функции распределения в максимуме, подставив формулу (20) в уравнение (19):

,

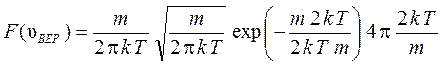. (21)

Из формул (20) и (21) следует, что при увеличении температуры или уменьшении массы молекулы максимум кривой смещается вправо и становится ниже (рис. 11). Однако площадь под кривой из условия нормировки (S = 1) сохраняется.

Зная функцию распределения F(υ), можно найти среднюю (арифметическую) скорость:

. (22)

Так, например, для T = 300 К средние скорости молекул кислорода и водорода равны соответственно 445 м/с и 1782 м/с.

Функции F(υ) можно придать другой вид, удобный при расчетах, если ввести относительную скорость: u = υ/υ_BEP.

Тогда , .

Если подставить получившиеся выражения для υ и dυв формулу dN/N = F(υ) d υ, то можно получить функцию распределения F(u) для относительной скорости:

,

, где 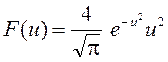. (23)

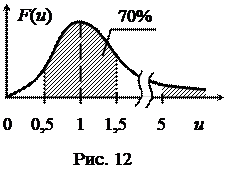
У 70% всех молекул скорость отличается от наиболее вероятной не более чем на 50% (рис. 12). А скорости, превышающие наиболее вероятную более чем в 5 раз, наблюдаются у одной из 12 млрд молекул.

Распределение Максвелла позволяет объяснить существование и рассеяние атмосферы планет. Чтобы покинуть Землю, молекула должна иметь скорость, превышающую вторую космическую (11,2 км/с). Эта скорость в 25 раз превышает наиболее вероятную скорость для молекул кислорода. Поэтому число покинувших Землю молекул кислорода очень мало. Однако легкие газы (водород, гелий) в основном рассеялись и остались «тяжелые» газы с небольшой скоростью молекул (азот, кислород, аргон, углекислый газ). Атмосферы сохранились у тех планет, у которых сильное тяготение (высокая вторая космическая скорость) и низкая температура (низкая скорость самих молекул). Атмосферы состоят в основном из «тяжелых» газов – азот, кислород, аммиак, метан и т.п.