Главная | Обратная связь

ТРИЗ-задание 11. Вакуум в науке, технике и быту

Использование пустоты (вакуума) вместо вещества – это один из законов развития технических систем и один из изобретательских приёмов. Наберите в любой поисковой системе в Интернете слова «вакуумный», «вакуумная», «вакуумное» и составьте список технических устройств и технологий с использованием вакуума.

Явления переноса

 

Явления переноса объединяют группу процессов, связанных с неоднородностями плотности, температуры или скорости упорядоченного перемещения отдельных слоёв вещества. При нарушении равновесия система стремится к нему вернуться, при этом в веществе возникает упорядоченный, направленный перенос массы (диффузия), импульса (внутреннее трение) и внутренней энергии (теплопроводность). Такие явления представляют собой необратимые процессы. Для рассмотрения явлений переноса необходимы два понятия из векторного анализа.

Градиент скалярной функции f (вектор) – это производная по направлению скорейшего (максимального) изменения этой функции. Например, градиент вдоль оси z: df/dz.

Поток вектора (скаляр). Пусть имеется поверхность S (рис. 15), в каждой точке которой можно установить нормали (пер- пендикуляры) .Пусть имеется векторноеполе , пронизывающее поверхностьS.Элементарный поток вектора dN равен скалярному произведению: . В частном случае, когда однородное поле пер­пендикулярно поверхности S, имеем N = aS.

Диффузия в газах

 

Диффузия – обусловленное тепловым движением самопроизвольное взаимное проникновение и перемешивание частиц соприкасающихся газов, жидкостей или твердых тел. Диффузия происходит в направлении уменьшения концентрации вещества (т.е. оттуда, где вещества больше, туда, где его меньше).

Процесс диффузии может происходить между различными агрегатными состояниями вещества. Например, в полупроводниковой технологии p-n-переходы создаются диффузией примеси, находящейся в газообразном или жидком состоянии, в твёрдый полупроводник (нагретый до 1000–1300 °С).

Установлено, что поток молекул, прошедших за время dt через площадку dS, перпендикулярную направлению переноса вещества, определяется законом Фика:

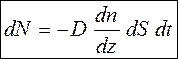, (26)

где dN – количество частиц (молекул); D – коэффициент диффузии; dn/dz – градиент концентрации в направлении оси z. Знак «минус» в формуле (26) обусловлен тем, что поток молекул направлен в сторону убывания концентрации. Знак «минус» компенсирует отрицательный знак градиента (рис. 16):

Умножив обе части формулы (26) на массу одной молекулы, получим выражение для потока массы и градиента плотности:

. (27)

Рассмотрим процесс диффузии в газах и найдем коэффициент диффузии. Пусть диффузия – стационарная, т.е. градиент концентрации (или плотности) является постоянным и не зависящим от времени. Рассмотрим площадку dS, перпендикулярную оси z (рис. 17). Пусть n₁ > n₂.

Из-за теплового движения молекулы будут переходить через площадку dS и слева направо, и справа налево. Однако из-за разности концентраций возникает диффузионный поток в направлении оси z. За время dt через площадку dS пройдут N молекул:

N = N ' - N ''. (28)

Поскольку тепловое движение хаотическое, тепловые скорости молекул равномерно распределены по трем осям x, y, z. Причем из 1/3 всех молекул, которые движутся вдоль оси z, одна половина движется в положительном направлении оси z, а другая половина – в отрицательном. Таким образом, в положительном направлении оси z движется 1/6 часть молекул.

За время dt до площадки dS долетят все движущиеся по направлению к ней молекулы, заключенные в элементе объёма с основанием dS и высотой áυñ dt. Умножив эти элементы объёма на концентрации молекул с одной и другой стороны площадки (n' и n''), получим количество молекул N ' и N '', прошедших через площадку dS в противоположных направлениях:

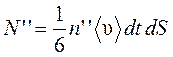, . (29)

Подставив уравнения (29) в формулу (28), получим:

(30)

Очевидно, что через площадку dS будут пролетать лишь те молекулы, которые испытали последнее соударение на различных расстояниях от dS. Значит, n' и n'' – это концентрации молекул на расстоянии длины свободного пробега l по обе стороны от площадки. Так как dn/dz – разность концентраций, приходящихся на единицу длины, то на расстоянии 2l разность концентраций равна

(31)

Подставив уравнение (31) в формулу (30), получим:

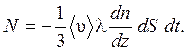(32)

Сравнивая формулы (26) и (32), находим коэффициент диффузии:

. (33)

Полученная формула (33) определяет коэффициент самодиффузии, т.е. диффузию молекул газа в среде того же газа.

Когда молекулы обеих компонент смеси неодинаковы по массе и эффективному сечению, коэффициент диффузии определяется более сложным выражением. Например, в смеси водорода и углекислого газа водород должен диффундировать быстрее, чем углекислый газ, так как средняя скорость молекул водорода почти в 5 раз выше, чем у углекислого газа, и кроме того, l(H₂) > l(СО₂). Это значит, что объём водорода, переносимого в одном направлении, больше объёма углекислого газа, переносимого в противоположном направлении. При этом неизбежно возникает разность давлений, которая влияет на процесс диффузии.