Главная | Обратная связь

Распределение Больцмана. Опыт Перрена

Атмосфера планеты находится в её гравитационном поле. Если бы этого поля не было, воздух рассеялся бы по космосу, а если бы не было теплового движения молекул газа, то молекулы атмосферного воздуха упали бы на Землю. Тяготение и тепловое движение приводят к такому стационарному состоянию атмосферы, при котором происходит убыль концентрации и давления газа с высотой.

Найдем, как изменяется давление с высотой. Для этого сделаем ряд упрощений: 1) Земля – идеальный шар; 2) атмосфера – идеальный газ; 3) температура на всех высотах одна и та же; 4) ускорение свободного падения не зависит от высоты; 5) молярная масса воздуха постоянна.

Пусть на поверхности Земли давление равно р₀, а на высоте h давление равно р (рис. 3). Воспользуемся формулой для давления p = rgh. При переходе от высоты h к высоте h + dh давление изменяется на величину – dp = rg dh. Знак «минус» говорит о том, что давление убывает с высотой. Плотность воздуха r найдем из уравнения Менделеева-Клапейрона:

Þ 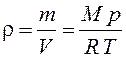; –dp= rgdh.

Получаем для изменения давления: .

Разделяем переменные: .

.

.

.

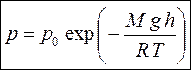. (8)

Формула (8) позволяет достаточно точно определять высоту по давлению. Например, погрешность барометрических высотомеров (альтиметров) для самолетов составляет около 10 м.

Если при выводе барометрической формулы учесть зависимость ускорения свободного падения от высоты, то получается формула, из которой следует, что даже на бесконечном удалении от Земли атмосферное давление не равно нулю. Так как это невозможно, то следует предположить, что атмосфера не находится в равновесном состоянии, а постепенно рассеивается в космическое пространство. Однако это рассеяние достаточно мало, так как атмосфера Земли существует несколько миллиардов лет.

Возьмем барометрическую формулу (8) и сделаем в ней следующие замены: p = nkT, M/R = M/(kN_A) = m/k, где m – масса одной молекулы; k – постоянная Больцмана. Предположим, что температуры на всех высотах одинаковы (Т = Т₀). Тогда

.

. (9)

Из формулы (9) следует, что процентное содержание (концентрация) легких газов в смеси возрастает с высотой (т.е. изменяется молярная масса воздуха).

Распределение Больцмана можно записать и в другом виде:

или . (10)

Формула (10) позволяет определить долю частиц от общего числа, которые в условиях теплового равновесия обладают потенциальной энергией e_p = mgh.

При помощи формулы (9) французский физик Перрен определил опытным путем постоянную Больцмана (зная которую можно вычислить число Авогадро). Перрен использовал эмульсии из частиц гуммигута диаметрами 0,1–5,5 мкм (гуммигýт – сок некоторых тропических деревьев, применяемый для изготовления жёлтых красок и лаков). При измерениях применялся микроскоп с очень малой глубиной резкости. В эмульсии непосредственно подсчитывалось число частиц в поле зрения микроскопа на разных высотах. При вычислениях учитывалась поправка на уменьшение веса за счёт силы Архимеда. Найденное значение постоянной Больцмана находилось в хорошем соответствии с результатами других исследователей, что доказывает применимость распределения Больцмана к броуновским частицам.